团体程序设计天梯赛-练习集 (L2-001 - L2-020)
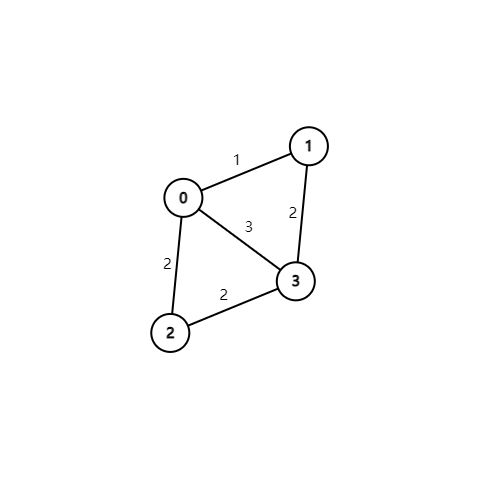
L2-001 紧急救援 最短路+路径打印
作为一个城市的应急救援队伍的负责人,你有一张特殊的全国地图。在地图上显示有多个分散的城市和一些连接城市的快速道路。每个城市的救援队数量和每一条连接两个城市的快速道路长度都标在地图上。当其他城市有紧急求助电话给你的时候,你的任务是带领你的救援队尽快赶往事发地,同时,一路上召集尽可能多的救援队。
输入格式:
输入第一行给出4个正整数N、M、S、D,其中N(2≤N≤500)是城市的个数,顺便假设城市的编号为0 ~ (N−1);M是快速道路的条数;S是出发地的城市编号;D是目的地的城市编号。
第二行给出N个正整数,其中第i个数是第i个城市的救援队的数目,数字间以空格分隔。随后的M行中,每行给出一条快速道路的信息,分别是:城市1、城市2、快速道路的长度,中间用空格分开,数字均为整数且不超过500。输入保证救援可行且最优解唯一。
输出格式:
第一行输出最短路径的条数和能够召集的最多的救援队数量。第二行输出从S到D的路径中经过的城市编号。数字间以空格分隔,输出结尾不能有多余空格。
输入样例:
4 5 0 3
20 30 40 10
0 1 1
1 3 2
0 3 3
0 2 2
2 3 2
输出样例:
2 60
0 1 3
分析:
Dijkstra基础应用,比模板单纯求最短路的基础上多了输出路径,路径条数以及多权重(路径相同时人数尽量大),路径只要存每个节点的前驱,然后倒着遍历一遍就行。其他就是一些小细节,看注释。优先队列默认为大顶堆priority_queue,这里需要改成小顶堆priority_queue
代码:
#includeL2-002 链表去重 模拟链表
给定一个带整数键值的链表 L,你需要把其中绝对值重复的键值结点删掉。即对每个键值 K,只有第一个绝对值等于 K 的结点被保留。同时,所有被删除的结点须被保存在另一个链表上。例如给定 L 为 21→-15→-15→-7→15,你需要输出去重后的链表 21→-15→-7,还有被删除的链表 -15→15。
输入格式:
输入在第一行给出 L 的第一个结点的地址和一个正整数 N(≤105,为结点总数)。一个结点的地址是非负的 5 位整数,空地址 NULL 用 −1 来表示。
随后 N 行,每行按以下格式描述一个结点:
地址 键值 下一个结点
其中地址是该结点的地址,键值是绝对值不超过104的整数,下一个结点是下个结点的地址。
输出格式:
首先输出去重后的链表,然后输出被删除的链表。每个结点占一行,按输入的格式输出。
输入样例:
00100 5
99999 -7 87654
23854 -15 00000
87654 15 -1
00000 -15 99999
00100 21 23854
输出样例:
00100 21 23854
23854 -15 99999
99999 -7 -1
00000 -15 87654
87654 15 -1
分析:
数据量不大,可以直接用数组模拟链表,地址当做数组下标,考察基本的删除操作和尾插法。
代码:
#includeL2-003 月饼 贪心
月饼是中国人在中秋佳节时吃的一种传统食品,不同地区有许多不同风味的月饼。现给定所有种类月饼的库存量、总售价、以及市场的最大需求量,请你计算可以获得的最大收益是多少。
注意:销售时允许取出一部分库存。样例给出的情形是这样的:假如我们有 3 种月饼,其库存量分别为 18、15、10 万吨,总售价分别为 75、72、45 亿元。如果市场的最大需求量只有 20 万吨,那么我们最大收益策略应该是卖出全部 15 万吨第 2 种月饼、以及 5 万吨第 3 种月饼,获得 72 + 45/2 = 94.5(亿元)。
输入格式:
每个输入包含一个测试用例。每个测试用例先给出一个不超过 1000 的正整数 N 表示月饼的种类数、以及不超过 500(以万吨为单位)的正整数 D 表示市场最大需求量。随后一行给出 N 个正数表示每种月饼的库存量(以万吨为单位);最后一行给出 N 个正数表示每种月饼的总售价(以亿元为单位)。数字间以空格分隔。
输出格式:
对每组测试用例,在一行中输出最大收益,以亿元为单位并精确到小数点后 2 位。
输入样例:
3 20
18 15 10
75 72 45
输出样例:
94.50
分析:
按照单价排序,优先选择单价最高的。库存量和总售价不一定为整数
代码:
#includeL2-004 这是二叉搜索树吗? 数据结构
一棵二叉搜索树可被递归地定义为具有下列性质的二叉树:对于任一结点,
- 其左子树中所有结点的键值小于该结点的键值;
- 其右子树中所有结点的键值大于等于该结点的键值;
- 其左右子树都是二叉搜索树。
所谓二叉搜索树的“镜像”,即将所有结点的左右子树对换位置后所得到的树。
给定一个整数键值序列,现请你编写程序,判断这是否是对一棵二叉搜索树或其镜像进行前序遍历的结果。
输入格式:
输入的第一行给出正整数 N(≤1000)。随后一行给出 N 个整数键值,其间以空格分隔。
输出格式:
如果输入序列是对一棵二叉搜索树或其镜像进行前序遍历的结果,则首先在一行中输出 YES ,然后在下一行输出该树后序遍历的结果。数字间有 1 个空格,一行的首尾不得有多余空格。若答案是否,则输出 NO。
输入样例 1:
7
8 6 5 7 10 8 11
输出样例 1:
YES
5 7 6 8 11 10 8
输入样例 2:
7
8 10 11 8 6 7 5
输出样例 2:
YES
11 8 10 7 5 6 8
输入样例 3:
7
8 6 8 5 10 9 11
输出样例 3:
NO
分析:
因为前序遍历是根左右,所以在插入某个孩子节点时,它的父节点肯定已经被插入了,又由于搜索树的限制关系(小的左边,大的右边),所以可以确定一棵唯一的二叉搜索树,然后对其进行两种不同的前序遍历,再分别与题目所给的序列比较即可。
代码:
#includeL2-005 集合相似度 STL
给定两个整数集合,它们的相似度定义为:Nc/Nt×100%。其中Nc是两个集合都有的不相等整数的个数,Nt是两个集合一共有的不相等整数的个数。你的任务就是计算任意一对给定集合的相似度。
输入格式:
输入第一行给出一个正整数N(≤50),是集合的个数。随后N行,每行对应一个集合。每个集合首先给出一个正整数M(≤104),是集合中元素的个数;然后跟M个[0,109]区间内的整数。
之后一行给出一个正整数K(≤2000),随后K行,每行对应一对需要计算相似度的集合的编号(集合从1到N编号)。数字间以空格分隔。
输出格式:
对每一对需要计算的集合,在一行中输出它们的相似度,为保留小数点后2位的百分比数字。
输入样例:
3
3 99 87 101
4 87 101 5 87
7 99 101 18 5 135 18 99
2
1 2
1 3
输出样例:
50.00%
33.33%
分析:
最多50个集合,预处理出全部的组合,C50 2=49∗25, 用set存放所有的集合,然后预处理的时候遍历两个set中较小的那个,在较大的中查找是否存在,将集合i和集合j共同拥有的数量存在both[i][j]中。Nc就是both[i][j],Nt就是两个集合size加起来再减掉both[i][j]。时间复杂度:25∗49∗10000∗log(10000)=49000000。
代码:
#include
}
printf("%.2lf%\n",num1*100.0/(num2-num1));
}
return 0;
}
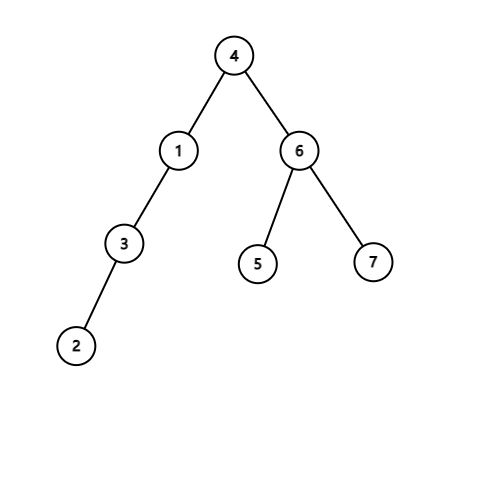
L2-006 树的遍历 数据结构
给定一棵二叉树的后序遍历和中序遍历,请你输出其层序遍历的序列。这里假设键值都是互不相等的正整数。
输入格式:
输入第一行给出一个正整数N(≤30),是二叉树中结点的个数。第二行给出其后序遍历序列。第三行给出其中序遍历序列。数字间以空格分隔。
输出格式:
在一行中输出该树的层序遍历的序列。数字间以1个空格分隔,行首尾不得有多余空格。
输入样例:
7
2 3 1 5 7 6 4
1 2 3 4 5 6 7
输出样例:
4 1 6 3 5 7 2
分析:
知道中序+后序或者前序,就能确定一棵唯一的二叉树。所以此题知道后序+中序,可以建立二叉树后层序遍历。由于后序是左右根,所以最后面的节点就是根,然后在中序中找到这个根的位置,左边就是左子树的范围,右边就是右子树的范围,递归处理即可。
代码:
#includeL2-007 家庭房产 并查集
给定每个人的家庭成员和其自己名下的房产,请你统计出每个家庭的人口数、人均房产面积及房产套数。
输入格式:
输入第一行给出一个正整数N(≤1000),随后N行,每行按下列格式给出一个人的房产:
编号 父 母 k 孩子1 ... 孩子k 房产套数 总面积
其中编号是每个人独有的一个4位数的编号;父和母分别是该编号对应的这个人的父母的编号(如果已经过世,则显示-1);k(0≤k≤5)是该人的子女的个数;孩子i是其子女的编号。
输出格式:
首先在第一行输出家庭个数(所有有亲属关系的人都属于同一个家庭)。随后按下列格式输出每个家庭的信息:
家庭成员的最小编号 家庭人口数 人均房产套数 人均房产面积
其中人均值要求保留小数点后3位。家庭信息首先按人均面积降序输出,若有并列,则按成员编号的升序输出。
输入样例:
10
6666 5551 5552 1 7777 1 100
1234 5678 9012 1 0002 2 300
8888 -1 -1 0 1 1000
2468 0001 0004 1 2222 1 500
7777 6666 -1 0 2 300
3721 -1 -1 1 2333 2 150
9012 -1 -1 3 1236 1235 1234 1 100
1235 5678 9012 0 1 50
2222 1236 2468 2 6661 6662 1 300
2333 -1 3721 3 6661 6662 6663 1 100
输出样例:
3
8888 1 1.000 1000.000
0001 15 0.600 100.000
5551 4 0.750 100.000
分析:
用并查集维护集合关系,由于要输出最小编号,合并时将较大的合并给较小的点,由于编号一共最多到9999,记录每个编号是否出现过,然后遍历一遍,将每个编号所拥有的房产等信息贡献给父节点。之后按照题目要求排序输出即可。
坑:编号可能会有0000
代码:
#includeL2-008 最长对称子串 字符串
对给定的字符串,本题要求你输出最长对称子串的长度。例如,给定Is PAT&TAP symmetric?,最长对称子串为s PAT&TAP s,于是你应该输出11。
输入格式:
输入在一行中给出长度不超过1000的非空字符串。
输出格式:
在一行中输出最长对称子串的长度。
输入样例:
Is PAT&TAP symmetric?
输出样例:
11
分析:
回文串问题,manacher模板题
代码:
#includeL2-009 抢红包 排序
没有人没抢过红包吧…… 这里给出N个人之间互相发红包、抢红包的记录,请你统计一下他们抢红包的收获。
输入格式:
输入第一行给出一个正整数N(≤104),即参与发红包和抢红包的总人数,则这些人从1到N编号。随后N行,第i行给出编号为i的人发红包的记录,格式如下:
K**N1P1⋯NKP**K
其中K(0≤K≤20)是发出去的红包个数,N**i是抢到红包的人的编号,P**i(>0)是其抢到的红包金额(以分为单位)。注意:对于同一个人发出的红包,每人最多只能抢1次,不能重复抢。
输出格式:
按照收入金额从高到低的递减顺序输出每个人的编号和收入金额(以元为单位,输出小数点后2位)。每个人的信息占一行,两数字间有1个空格。如果收入金额有并列,则按抢到红包的个数递减输出;如果还有并列,则按个人编号递增输出。
输入样例:
10
3 2 22 10 58 8 125
5 1 345 3 211 5 233 7 13 8 101
1 7 8800
2 1 1000 2 1000
2 4 250 10 320
6 5 11 9 22 8 33 7 44 10 55 4 2
1 3 8800
2 1 23 2 123
1 8 250
4 2 121 4 516 7 112 9 10
输出样例:
1 11.63
2 3.63
8 3.63
3 2.11
7 1.69
6 -1.67
9 -2.18
10 -3.26
5 -3.26
4 -12.32
分析:
就是细节题,题目让你干什么就干什么。结构体中自定义排序规则
代码:
#includeL2-010 排座位 dfs
布置宴席最微妙的事情,就是给前来参宴的各位宾客安排座位。无论如何,总不能把两个死对头排到同一张宴会桌旁!这个艰巨任务现在就交给你,对任何一对客人,请编写程序告诉主人他们是否能被安排同席。
输入格式:
输入第一行给出3个正整数:N(≤100),即前来参宴的宾客总人数,则这些人从1到N编号;M为已知两两宾客之间的关系数;K为查询的条数。随后M行,每行给出一对宾客之间的关系,格式为:宾客1 宾客2 关系,其中关系为1表示是朋友,-1表示是死对头。注意两个人不可能既是朋友又是敌人。最后K行,每行给出一对需要查询的宾客编号。
这里假设朋友的朋友也是朋友。但敌人的敌人并不一定就是朋友,朋友的敌人也不一定是敌人。只有单纯直接的敌对关系才是绝对不能同席的。
输出格式:
对每个查询输出一行结果:如果两位宾客之间是朋友,且没有敌对关系,则输出No problem;如果他们之间并不是朋友,但也不敌对,则输出OK;如果他们之间有敌对,然而也有共同的朋友,则输出OK but...;如果他们之间只有敌对关系,则输出No way。
输入样例:
7 8 4
5 6 1
2 7 -1
1 3 1
3 4 1
6 7 -1
1 2 1
1 4 1
2 3 -1
3 4
5 7
2 3
7 2
输出样例:
No problem
OK
OK but...
No way
分析:
N≤100,说明可以直接建图后进行dfs遍历,只遍历边权为1的点,如果可以从a走到b,说明有共同朋友,再判断mp[a][b]是否为-1即可。其他情况类似。
代码:
#include L2-011 玩转二叉树 数据结构
给定一棵二叉树的中序遍历和前序遍历,请你先将树做个镜面反转,再输出反转后的层序遍历的序列。所谓镜面反转,是指将所有非叶结点的左右孩子对换。这里假设键值都是互不相等的正整数。
输入格式:
输入第一行给出一个正整数N(≤30),是二叉树中结点的个数。第二行给出其中序遍历序列。第三行给出其前序遍历序列。数字间以空格分隔。
输出格式:
在一行中输出该树反转后的层序遍历的序列。数字间以1个空格分隔,行首尾不得有多余空格。
输入样例:
7
1 2 3 4 5 6 7
4 1 3 2 6 5 7
输出样例:
4 6 1 7 5 3 2
分析:
就是两种遍历方式求另外一种,PTA好喜欢这种题,镜面翻转其实就是在求层序的时候反着放入队列就行。
代码:
#includeL2-013 红色警报 并查集
战争中保持各个城市间的连通性非常重要。本题要求你编写一个报警程序,当失去一个城市导致国家被分裂为多个无法连通的区域时,就发出红色警报。注意:若该国本来就不完全连通,是分裂的k个区域,而失去一个城市并不改变其他城市之间的连通性,则不要发出警报。
输入格式:
输入在第一行给出两个整数N(0 < N ≤ 500)和M(≤ 5000),分别为城市个数(于是默认城市从0到N-1编号)和连接两城市的通路条数。随后M行,每行给出一条通路所连接的两个城市的编号,其间以1个空格分隔。在城市信息之后给出被攻占的信息,即一个正整数K和随后的K个被攻占的城市的编号。
注意:输入保证给出的被攻占的城市编号都是合法的且无重复,但并不保证给出的通路没有重复。
输出格式:
对每个被攻占的城市,如果它会改变整个国家的连通性,则输出Red Alert: City k is lost!,其中k是该城市的编号;否则只输出City k is lost.即可。如果该国失去了最后一个城市,则增加一行输出Game Over.。
输入样例:
5 4
0 1
1 3
3 0
0 4
5
1 2 0 4 3
输出样例:
City 1 is lost.
City 2 is lost.
Red Alert: City 0 is lost!
City 4 is lost.
City 3 is lost.
Game Over.
分析:
每次删去一个点,可以用一个数组记录标记被删去的点,每删去一个点,对所有不包含被删去点的边求一次并查集,检查有几个集合,如果比之前多则说明有国家被分裂了,注意已经被消灭的城市不会算入一个集合。
代码:
#includeL2-014 列车调度 STL
火车站的列车调度铁轨的结构如下图所示。
两端分别是一条入口(Entrance)轨道和一条出口(Exit)轨道,它们之间有N条平行的轨道。每趟列车从入口可以选择任意一条轨道进入,最后从出口离开。在图中有9趟列车,在入口处按照{8,4,2,5,3,9,1,6,7}的顺序排队等待进入。如果要求它们必须按序号递减的顺序从出口离开,则至少需要多少条平行铁轨用于调度?
输入格式:
输入第一行给出一个整数N (2 ≤ N ≤105),下一行给出从1到N的整数序号的一个重排列。数字间以空格分隔。
输出格式:
在一行中输出可以将输入的列车按序号递减的顺序调离所需要的最少的铁轨条数。
输入样例:
9
8 4 2 5 3 9 1 6 7
输出样例:
4
分析:
可以这样调度:先查看当前所有轨道的最左边火车编号是否小于当前编号,插入到最小的比当前火车编号大的火车后,如果不存在则开辟新轨道。可知,轨道的最左端火车编号一定是随轨道下标而递增的,可以用二分查找快速找到那条轨道。当然,可以用set更为方便。
代码:
#includeL2-015 互评成绩 排序
学生互评作业的简单规则是这样定的:每个人的作业会被k个同学评审,得到k个成绩。系统需要去掉一个最高分和一个最低分,将剩下的分数取平均,就得到这个学生的最后成绩。本题就要求你编写这个互评系统的算分模块。
输入格式:
输入第一行给出3个正整数N(3 < N ≤104,学生总数)、k(3 ≤ k ≤ 10,每份作业的评审数)、M(≤ 20,需要输出的学生数)。随后N行,每行给出一份作业得到的k个评审成绩(在区间[0, 100]内),其间以空格分隔。
输出格式:
按非递减顺序输出最后得分最高的M个成绩,保留小数点后3位。分数间有1个空格,行首尾不得有多余空格。
输入样例:
6 5 3
88 90 85 99 60
67 60 80 76 70
90 93 96 99 99
78 65 77 70 72
88 88 88 88 88
55 55 55 55 55
输出样例:
87.667 88.000 96.000
代码:
#includeL2-016 愿天下有情人都是失散多年的兄妹 dfs
呵呵。大家都知道五服以内不得通婚,即两个人最近的共同祖先如果在五代以内(即本人、父母、祖父母、曾祖父母、高祖父母)则不可通婚。本题就请你帮助一对有情人判断一下,他们究竟是否可以成婚?
输入格式:
输入第一行给出一个正整数()N(2≤N≤104),随后N行,每行按以下格式给出一个人的信息:
本人ID 性别 父亲ID 母亲ID
其中ID是5位数字,每人不同;性别M代表男性、F代表女性。如果某人的父亲或母亲已经不可考,则相应的ID位置上标记为-1。
接下来给出一个正整数K,随后K行,每行给出一对有情人的ID,其间以空格分隔。
注意:题目保证两个人是同辈,每人只有一个性别,并且血缘关系网中没有乱伦或隔辈成婚的情况。
输出格式:
对每一对有情人,判断他们的关系是否可以通婚:如果两人是同性,输出Never Mind;如果是异性并且关系出了五服,输出Yes;如果异性关系未出五服,输出No。
输入样例:
24
00001 M 01111 -1
00002 F 02222 03333
00003 M 02222 03333
00004 F 04444 03333
00005 M 04444 05555
00006 F 04444 05555
00007 F 06666 07777
00008 M 06666 07777
00009 M 00001 00002
00010 M 00003 00006
00011 F 00005 00007
00012 F 00008 08888
00013 F 00009 00011
00014 M 00010 09999
00015 M 00010 09999
00016 M 10000 00012
00017 F -1 00012
00018 F 11000 00013
00019 F 11100 00018
00020 F 00015 11110
00021 M 11100 00020
00022 M 00016 -1
00023 M 10012 00017
00024 M 00022 10013
9
00021 00024
00019 00024
00011 00012
00022 00018
00001 00004
00013 00016
00017 00015
00019 00021
00010 00011
输出样例:
Never Mind
Yes
Never Mind
No
Yes
No
Yes
No
No
分析
先跑一遍dfs标记第一个人的所有五代内的长辈,然后再dfs一遍第二个人的所有五代内的长辈,检查是否有重复。有个坑点就是:父母的性别都是已知的,但是可能不会告诉你父母的祖辈情况,所以要同时记录父母的性别,否则父母性别默认初始值都是相同的了。还有个我自己的问题,直接在结构体内赋值的方式进行初始化,这样是不可行的,正确方法是要么循环遍历初始化,要么写一个构造函数。
代码
#include L2-017 人以群分 水题
社交网络中我们给每个人定义了一个“活跃度”,现希望根据这个指标把人群分为两大类,即外向型(outgoing,即活跃度高的)和内向型(introverted,即活跃度低的)。要求两类人群的规模尽可能接近,而他们的总活跃度差距尽可能拉开。
输入格式:
输入第一行给出一个正整数N(2≤N≤105)。随后一行给出N个正整数,分别是每个人的活跃度,其间以空格分隔。题目保证这些数字以及它们的和都不会超过231。
输出格式:
按下列格式输出:
Outgoing #: N1
Introverted #: N2
Diff = N3
其中N1是外向型人的个数;N2是内向型人的个数;N3是两群人总活跃度之差的绝对值。
输入样例1:
10
23 8 10 99 46 2333 46 1 666 555
输出样例1:
Outgoing #: 5
Introverted #: 5
Diff = 3611
输入样例2:
13
110 79 218 69 3721 100 29 135 2 6 13 5188 85
输出样例2:
Outgoing #: 7
Introverted #: 6
Diff = 9359
分析:
要先保证人数平均再保证差值尽量大,那么就排序后平均分成两份的差值会最大,如果人数为奇数,中间值分给外向的人群可以使得差值最大。
代码:
#includeL2-018 多项式A除以B 模拟
这仍然是一道关于A/B的题,只不过A和B都换成了多项式。你需要计算两个多项式相除的商Q和余R,其中R的阶数必须小于B的阶数。
输入格式:
输入分两行,每行给出一个非零多项式,先给出A,再给出B。每行的格式如下:
N e[1] c[1] ... e[N] c[N]
其中N是该多项式非零项的个数,e[i]是第i个非零项的指数,c[i]是第i个非零项的系数。各项按照指数递减的顺序给出,保证所有指数是各不相同的非负整数,所有系数是非零整数,所有整数在整型范围内。
输出格式:
分两行先后输出商和余,输出格式与输入格式相同,输出的系数保留小数点后1位。同行数字间以1个空格分隔,行首尾不得有多余空格。注意:零多项式是一个特殊多项式,对应输出为0 0 0.0。但非零多项式不能输出零系数(包括舍入后为0.0)的项。在样例中,余多项式其实有常数项-1/27,但因其舍入后为0.0,故不输出。
输入样例:
4 4 1 2 -3 1 -1 0 -1
3 2 3 1 -2 0 1
输出样例:
3 2 0.3 1 0.2 0 -1.0
1 1 -3.1
分析:
模拟手算多项式除法即可,注意细节
代码:
#includeL2-019 悄悄关注 STL
新浪微博上有个“悄悄关注”,一个用户悄悄关注的人,不出现在这个用户的关注列表上,但系统会推送其悄悄关注的人发表的微博给该用户。现在我们来做一回网络侦探,根据某人的关注列表和其对其他用户的点赞情况,扒出有可能被其悄悄关注的人。
输入格式:
输入首先在第一行给出某用户的关注列表,格式如下:
人数N 用户1 用户2 …… 用户N
其中N是不超过5000的正整数,每个用户i(i=1, …, N)是被其关注的用户的ID,是长度为4位的由数字和英文字母组成的字符串,各项间以空格分隔。
之后给出该用户点赞的信息:首先给出一个不超过10000的正整数M,随后M行,每行给出一个被其点赞的用户ID和对该用户的点赞次数(不超过1000),以空格分隔。注意:用户ID是一个用户的唯一身份标识。题目保证在关注列表中没有重复用户,在点赞信息中也没有重复用户。
输出格式:
我们认为被该用户点赞次数大于其点赞平均数、且不在其关注列表上的人,很可能是其悄悄关注的人。根据这个假设,请你按用户ID字母序的升序输出可能是其悄悄关注的人,每行1个ID。如果其实并没有这样的人,则输出“Bing Mei You”。
输入样例1:
10 GAO3 Magi Zha1 Sen1 Quan FaMK LSum Eins FatM LLao
8
Magi 50
Pota 30
LLao 3
Ammy 48
Dave 15
GAO3 31
Zoro 1
Cath 60
输出样例1:
Ammy
Cath
Pota
输入样例2:
11 GAO3 Magi Zha1 Sen1 Quan FaMK LSum Eins FatM LLao Pota
7
Magi 50
Pota 30
LLao 48
Ammy 3
Dave 15
GAO3 31
Zoro 29
输出样例2:
Bing Mei You
分析:
map记录一下哪些名字出现过,再用一个map记录点赞情况并求出平均值,遍历记录点赞记录的map,将满足条件的名字放入vector,排序输出。
代码:
#include L2-020 功夫传人 dfs
一门武功能否传承久远并被发扬光大,是要看缘分的。一般来说,师傅传授给徒弟的武功总要打个折扣,于是越往后传,弟子们的功夫就越弱…… 直到某一支的某一代突然出现一个天分特别高的弟子(或者是吃到了灵丹、挖到了特别的秘笈),会将功夫的威力一下子放大N倍 —— 我们称这种弟子为“得道者”。
这里我们来考察某一位祖师爷门下的徒子徒孙家谱:假设家谱中的每个人只有1位师傅(除了祖师爷没有师傅);每位师傅可以带很多徒弟;并且假设辈分严格有序,即祖师爷这门武功的每个第i代传人只能在第i-1代传人中拜1个师傅。我们假设已知祖师爷的功力值为Z,每向下传承一代,就会减弱r%,除非某一代弟子得道。现给出师门谱系关系,要求你算出所有得道者的功力总值。
输入格式:
输入在第一行给出3个正整数,分别是:N(≤105)——整个师门的总人数(于是每个人从0到N−1编号,祖师爷的编号为0);Z——祖师爷的功力值(不一定是整数,但起码是正数);r ——每传一代功夫所打的折扣百分比值(不超过100的正数)。接下来有N行,第i行(i=0,⋯,N−1)描述编号为i的人所传的徒弟,格式为:
K**i ID[1] ID[2] ⋯ ID[K**i]
其中K**i是徒弟的个数,后面跟的是各位徒弟的编号,数字间以空格间隔。K**i为零表示这是一位得道者,这时后面跟的一个数字表示其武功被放大的倍数。
输出格式:
在一行中输出所有得道者的功力总值,只保留其整数部分。题目保证输入和正确的输出都不超过1010。
输入样例:
10 18.0 1.00
3 2 3 5
1 9
1 4
1 7
0 7
2 6 1
1 8
0 9
0 4
0 3
输出样例:
404
分析:
由于每个徒弟严格只会跟一个高一辈的师傅,直接保存每个人的徒弟,然后dfs一遍就行,标记一下超级徒弟dfs的时候判断一下就行,超级徒弟就是叶子节点。
代码:
#include