HDU (1710)Binary Tree Traversals
In a preorder traversal of the vertices of T, we visit the root r followed by visiting the vertices of T1 in preorder, then the vertices of T2 in preorder.
In an inorder traversal of the vertices of T, we visit the vertices of T1 in inorder, then the root r, followed by the vertices of T2 in inorder.
In a postorder traversal of the vertices of T, we visit the vertices of T1 in postorder, then the vertices of T2 in postorder and finally we visit r.
Now you are given the preorder sequence and inorder sequence of a certain binary tree. Try to find out its postorder sequence.
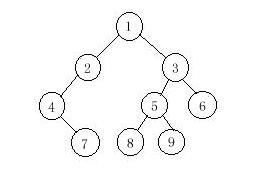
//这题是根据二叉树的前序和中序求后序,第一次接触,研究了挺久的
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#define N 1003
typedef struct node
{
int n;
struct node *l,*r;
}BT;
BT* ct(int *f,int *s,int fl,int fr,int sl,int sr)
{
int l,n;
BT *p=(BT *)malloc(sizeof(BT));
p->n=f[fl];
if(fl==fr)
{
p->l=p->r=NULL;
return p;
}
for(l=sl;l<=sr;l++)
if(s[l]==f[fl])
break;
n=l-sl;
if(l==sl&&sr-sl>0) //找到的节点在第一位,且后面有节点
{
p->l=NULL;
p->r=ct(f,s,fl+1,fr,l+1,sr);
return p;
}
else
if(l==sr&&sr-sl>0)//找到的节点在最后面,且前面有节点
{
p->r=NULL;
p->l=ct(f,s,fl+1,fr,sl,sr-1);
return p;
}
p->l=ct(f,s,fl+1,fl+n,sl,l-1);//这里可能还可以优化
p->r=ct(f,s,fl+n+1,fr,l+1,sr);
return p;
}
void disp(BT *p,int c)
{
if(p->l!=NULL)
disp(p->l,2);
if(p->r!=NULL)
disp(p->r,2);
if(c!=1)
printf("%d ",p->n);
else
printf("%d\n",p->n);//第一次是忘记加换行符了,PE了一次,唉!
}
int main()
{
int i,n,f[N],s[N];
BT* p=NULL;
while(scanf("%d",&n)!=EOF)
{
for(i=0;i<n;i++)
scanf("%d",&f[i]);//输入前序
for(i=0;i<n;i++)
scanf("%d",&s[i]);//输入后序
p=ct(f,s,0,n-1,0,n-1);//还原这课树
disp(p,1);//后序遍历
}
return 0;
}
#include <stdio.h>//在上面的代码提交了几秒之后,我突发奇想,改成了以下代码
#include <string.h>//想到书上说的不用递归的遍历,用栈来模仿、
#include <stdlib.h>//还好。成功AC了,上面的代码是31MS,这个代码是15MS,而且更短,更节省内存
#define N 1003 //不知道0Ms的代码怎么样的,佩服!
void ct(int *f,int *s,int fl,int fr,int sl,int sr,int c)
{
int l,n;
if(fl==fr)
{ if(c!=1)
printf("%d ",f[fl]);
else
printf("%d\n",f[fl]);
return ;
}
for(l=sl;l<=sr;l++)
if(s[l]==f[fl])
break;
n=l-sl;
if(l==sl&&sr-sl>0)
{
ct(f,s,fl+1,fr,l+1,sr,2);
if(c!=1)
printf("%d ",f[fl]);
else
printf("%d\n",f[fl]);
return ;
}
else
if(l==sr&&sr-sl>0)
{
ct(f,s,fl+1,fr,sl,sr-1,2);
if(c!=1)
printf("%d ",f[fl]);
else
printf("%d\n",f[fl]);
return ;
}
ct(f,s,fl+1,fl+n,sl,l-1,2);
ct(f,s,fl+n+1,fr,l+1,sr,2);
if(c!=1)
printf("%d ",f[fl]);
else
printf("%d\n",f[fl]);
return ;
}
int main()
{
int i,n,f[N],s[N];
while(scanf("%d",&n)!=EOF)
{
for(i=0;i<n;i++)
scanf("%d",&f[i]);
for(i=0;i<n;i++)
scanf("%d",&s[i]);
ct(f,s,0,n-1,0,n-1,1);
}
return 0;
}
-----江财小子