使用霍夫曼编码的图像压缩二

继续前面章节的介绍

为什么要使用两个结构数组？

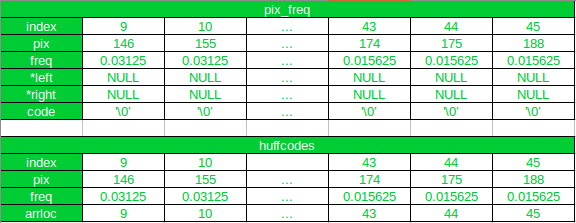
最初，struct array pix_freq以及 struct array huffcodes将仅包含 Huffman Tree 中所有叶节点的信息。

结构数组pix_freq将用于存储霍夫曼树的所有节点，数组huffcodes将用作更新（和排序）树。

请记住，每次迭代中只会对huffcodes进行排序，而不是pix_freq

通过组合最低频率的两个节点创建的新节点，在每次迭代中，将附加到pix_freq数组的末尾，也附加到huffcodes数组。

但是数组huffcodes在加入新节点后，会按照出现的概率重新排序。

数组pix_freq中新节点的位置将存储在struct huffcode的arrloc字段中。将指针分配给新节点的左右子节点时将使用arrloc字段。

第 4 步继续……

现在，如果有N 个叶子节点，则整个哈夫曼树的节点总数将等于2N-1

并且在两个节点合并并被新的父节点替换后，节点的数量在每次迭代中减少1 。因此，数组huffcodes有一定长度的节点就足够了，这些节点将用作更新和排序的霍夫曼节点。

int totalnodes = 2 * nodes - 1;
pix_freq = (struct pixfreq*)malloc(sizeof(struct pixfreq) * totalnodes);
huffcodes = (struct huffcode*)malloc(sizeof(struct huffcode) * nodes);

步骤 5用叶节点的信息
初始化两个数组pix_freq和huffcodes 。

j = 0;
int totpix = height * width;
float tempprob;
for (i = 0; i < 256; i++) 
{
    if (hist[i] != 0)
    {
          
        // pixel intensity value
        huffcodes[j].pix = i; 
        pix_freq[j].pix = i;
          
        // location of the node
        // in the pix_freq array
        huffcodes[j].arrloc = j; 
          
        // probability of occurrence
        tempprob = (float)hist[i] / (float)totpix; 
        pix_freq[j].freq = tempprob;
        huffcodes[j].freq = tempprob;
          
        // Declaring the child of 
        // leaf node as NULL pointer
        pix_freq[j].left = NULL; 
        pix_freq[j].right = NULL;
          
        // initializing the code
        // word as end of line
        pix_freq[j].code[0] = '\0'; 
        j++;
    }
}

Step 6根据像素强度值出现的概率对huffcodes
数组进行排序

请注意，有必要对huffcodes数组进行排序，而不是pix_freq数组，因为我们已经将像素值的位置存储在huffcodes数组的arrloc字段中。

// Sorting the histogram
struct huffcode temphuff;
  
// Sorting w.r.t probability 
// of occurrence
for (i = 0; i < nodes; i++)
 {
    for (j = i + 1; j < nodes; j++) 
{
        if (huffcodes[i].freq < huffcodes[j].freq) 
{
            temphuff = huffcodes[i];
            huffcodes[i] = huffcodes[j];
            huffcodes[j] = temphuff;
        }
    }
}

第 7 步
构建哈夫曼树

我们首先组合出现概率最低的两个节点，然后用新节点替换这两个节点。这个过程一直持续到我们有一个根节点。形成的第一个父节点将存储在数组pix_freq中的索引节点，后续获得的父节点将存储在索引值较高的位置。

// Building Huffman Tree
  
float sumprob;
int sumpix;
int n = 0, k = 0;
int nextnode = nodes;
  
// Since total number of 
// nodes in Huffman Tree 
// is 2*nodes-1
while (n < nodes - 1) 
{
      
    // Adding the lowest 
    // two probabilities
    sumprob = huffcodes[nodes - n - 1].freq + huffcodes[nodes - n - 2].freq;
    sumpix = huffcodes[nodes - n - 1].pix + huffcodes[nodes - n - 2].pix;
      
    // Appending to the pix_freq Array
    pix_freq[nextnode].pix = sumpix;
    pix_freq[nextnode].freq = sumprob;
    pix_freq[nextnode].left = &pix_freq[huffcodes[nodes - n - 2].arrloc];
      
    // arrloc points to the location
    // of the child node in the
    // pix_freq array
    pix_freq[nextnode].right = &pix_freq[huffcodes[nodes - n - 1].arrloc];
    pix_freq[nextnode].code[0] = '\0';
      
    // Using sum of the pixel values as 
    // new representation for the new node
    // since unlike strings, we cannot 
    // concatenate because the pixel values 
    // are stored as integers. However, if we
    // store the pixel values as strings
    // we can use the concatenated string as 
    // a representation of the new node.
    i = 0;
      
    // Sorting and Updating the huffcodes 
    // array simultaneously New position
    // of the combined node
    while (sumprob <= huffcodes[i].freq)
        i++;
          
    // Inserting the new node in
    // the huffcodes array
    for (k = nnz; k >= 0; k--) 
    {
        if (k == i)
        {
            huffcodes[k].pix = sumpix;
            huffcodes[k].freq = sumprob;
            huffcodes[k].arrloc = nextnode;
        }
        else if (k > i)
          
            // Shifting the nodes below
            // the new node by 1
            // For inserting the new node 
            // at the updated position k
            huffcodes[k] = huffcodes[k - 1];
    }
    n += 1;
    nextnode += 1;
}

这段代码是如何工作的？

让我们看一个例子：

最初

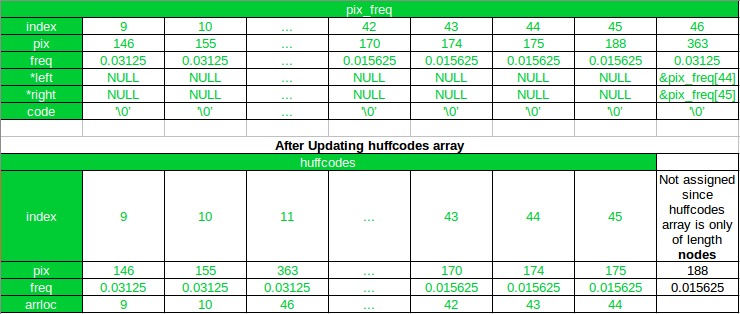
第一次迭代后

如您所见，在第一次迭代后，新节点已附加到pix_freq数组，其索引为 46。在 huffcode 中，新节点已在排序后添加到其新位置，arrloc指向索引pix_freq数组中的新节点。另外，请注意， huffcodes数组中新节点（索引 11 处）之后的所有数组元素都已移动 1，并且像素值为 188 的数组元素被排除在更新后的数组中。

现在，在下一次（第 2 次）迭代中，170 和 174 将被合并，因为 175 和 188 已经合并。
根据变量节点和n的最低两个节点的索引是

left_child_index=(nodes-n-2)

和

right_child_index=(nodes-n-1)

在第二次迭代中，n 的值为 1（因为 n 从 0 开始）。

对于值为 170 的节点

left_child_index=46-1-2=43

对于值为 174 的节点

right_child_index=46-1-1=44

因此，即使 175 仍然是更新数组的最后一个元素，它也会被排除在外。

在此代码中要注意的另一件事是，如果在任何后续迭代中，在第一次迭代中形成的新节点是另一个新节点的子节点，则可以使用访问在第一次迭代中获得的指向新节点的指针arrloc存储在huffcodes数组中，就像在这行代码中所做的那样

pix_freq[nextnode].right = &pix_freq[huffcodes[nodes - n - 1].arrloc];