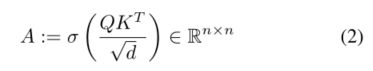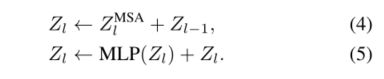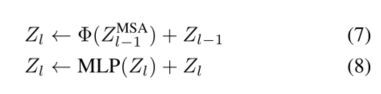Skip-Attention学习笔记
Skip-Attention学习笔记
Skip-Attention: Improving Vision Transformers by Paying Less Attention
Abstract
这项工作旨在提高视觉变换器(ViT)的效率。虽然ViT在每一层中都使用计算成本高昂的自我关注操作,但我们发现这些操作在各层之间高度相关——这是一种关键的冗余,会导致不必要的计算。基于这一观察,我们提出了SKIPAT,这是一种重用来自前一层的自我注意力计算来近似一个或多个后续层的注意力的方法。为了确保跨层重用自我关注块不会降低性能,我们引入了一个简单的参数函数,该函数在计算速度更快的同时,性能优于基线变换器。我们在ImageNet-1K上的图像分类和自监督学习、ADE20K上的语义分割、SIDD上的图像去噪以及DA-VIS上的视频去噪方面展示了我们的方法的有效性。我们在所有这些任务中以相同或更高的精度水平实现了吞吐量的提高。
1. Introduction
变压器架构[50]由于其简单性、可扩展性和广泛的应用范围,已成为一个重要且极具影响力的模型家族。虽然最初起源于自然语言处理(NLP)领域,但随着视觉变换器(ViT)的出现[15],这已成为计算机视觉中的标准架构,在从表示学习、语义分割、对象检测和视频理解等任务上设置了各种最先进的(SoTA)性能[4,5,18,30,31]。
然而,变换器的原始公式包括关于输入令牌数量的二次计算复杂性。考虑到这个数字通常从图像分类的142到图像去噪的1282=16K,这个对内存和计算的限制严重限制了它的适用性。为了解决这个问题,有三种方法。第一种方法利用输入令牌之间的冗余,并通过有效采样(例如丢弃或合并冗余令牌)简单地减少计算[17,46,63]。然而,这意味着ViT的最终输出在空间上不是连续的,因此不能在图像级应用之外使用,例如语义分割或对象定位。第二组方法旨在廉价地估计注意力计算,但通常以性能降低为代价[10,65]。最后,另一系列工作旨在将卷积架构与变换器合并,产生混合架构[29,29,39]。虽然这些方法提高了速度,但它们并没有解决二次复杂度这一根本问题,而且往往会引入大量的设计选择(本质上是变压器和网络控制器的结合)。
在这项工作中,我们提出了一种迄今为止尚未探索的新方法来解决这个问题:简单地用一个更快、更简单的参数函数来逼近变压器的计算昂贵的块。为了得到这个解决方案,我们首先彻底分析了ViT的关键多头自我关注(MSA)块。通过该分析,我们发现CLS令牌对空间补丁的关注在变换器的块之间具有非常高的相关性,从而导致不必要的计算。这促使我们的方法利用模型早期部分的注意力,并简单地将其重新用于更深的块——基本上“跳过”后续SA计算,而不是在每一层重新计算它们。
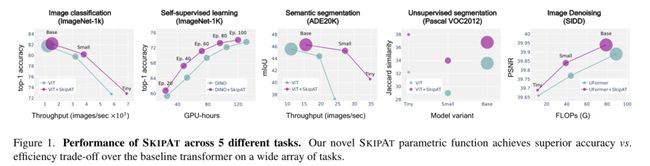
基于此,我们进一步探索是否可以通过重用先前层的表示来跳过层的整个MSA块。我们发现,受ResneXt深度卷积启发的简单参数函数[62]可以超过基线性能,同时在吞吐量和FLOP方面计算速度更快。我们的方法是通用的,可以在任何情况下应用于ViT:图1显示,与各种任务、数据集和模型大小的基线变换器相比,我们的用于跳过注意力的新参数函数(SKIPAT)实现了更高的精度和效率权衡。
总之,我们的主要贡献如下:
1、我们提出了一种新的插件模块,它可以放置在任何ViT架构中,以减少昂贵的 O ( n 2 ) O(n^2) O(n2)自我注意计算(第3.3小节)
2、我们在ImageNet、Pascal-VOC2012、SIDD、DA VIS和ADE20K(在后者中,我们获得了40%的加速率)的吞吐量方面达到了最先进的性能(第4节)
3、我们进一步证明了我们的方法的通用性,即获得了26%的自监督预训练时间减少(无下游精度损失),并证明了优越的设备延迟(第4.2节,第4.1节)
4、最后,我们分析了性能增益的来源,并广泛讨论了我们的方法,以提供一个可用于权衡精度和吞吐量的模型族(第4.6小节)
2. Related Work
已经从多个方面努力提高视觉变换器(ViT)的效率[15]:
Token sampling
通过在标记化步骤[21,66]期间重组图像、通过训练修剪冗余标记[26,46]或在推断[7,17,43,63]处动态地修剪冗余标记来提高效率。尽管令牌采样方法在降低图像分类中的计算成本方面很有效,但它们很难适用于密集的预测任务,例如语义分割和图像去噪,其中输出图像应该是空间连续的。我们的方法是对这些工作线的补充,并在实验中验证了它们。此外,考虑到我们在整个网络中保持表示所有令牌,我们的方法适用于分类和密集预测任务。
Hybrid architectures
通过采用Unifier[29]中的MobileNet块、MobileViT[35]中的MobileNetV2块或在图像标记化步骤[19,59]中使用卷积堆栈,将高效卷积模块集成到视觉变换器[32,36,39]中。类似地,我们使用卷积来加速视觉变换器,然而,与[29,35,36,39]中的定制块不同,我们坚持原始的变换器架构,并通过卷积近似整个MSA计算。
Efficient attentions
通过对键和值嵌入的全局下采样[54,59]、在本地窗口中执行自我关注[31]、在本地和全局自我关注之间交替[10,35,39]或用简单的池替换自我关注[65],解决视觉转换器中自我关注操作的二次成本。然而,减少对局部邻域的自我关注阻碍了他们对长距离依赖关系建模的能力,并导致在适度加速的情况下性能显著下降[69]。此外,一些引入的操作没有有效的支持,例如Swin[31]中的循环移位,限制了它们在延迟方面的实际效率增益。与此不同的是,我们的方法在几个块中依赖于强而低效的自我注意算子,而在其他块中则依赖于更轻而准确的注意力估计。由于估计器仅依赖于标准卷积运算,我们的方法转化为实际延迟增益。与本文相关,[55,60,64]观察到NLP任务注意图中的冗余。然而,我们不是简单地复制注意力图[60,64],而是提出了一种有效的参数函数,如我们所示,该函数对于实现高吞吐量,同时保持视觉任务中的高模型性能至关重要。
Hierarchical architectures
将分层表示作为计算机视觉中的一个长期原则引入视觉变换器[19,31,40,54,69]。使用多尺度表示显著提高了各向同性架构(如ViT)的内存和计算成本。最近,这一想法已扩展到具有U-Net[57]或多分支结构[20]的更复杂的架构。我们的工作是对这些工作的补充,因为它们没有解决降低自我注意算子的二次复杂性的根本问题。我们通过实验验证了我们的方法在这种各向同性和分层架构上的有效性。
3. Skip-Attention
3.1. Preliminaries
**Vision Transformer **
设 x ∈ R h × w × c x∈R^{h×w×c} x∈Rh×w×c为输入图像,其中h×w为空间分辨率,c为通道数。首先将图像标记为 n = h w / p 2 n=hw/p^2 n=hw/p2个不重叠的面片,其中p×p是面片大小。使用线性层将每个面片投影到嵌入 z i ∈ R d z_i∈R^d zi∈Rd中以获得标记化图像:
这里,“;”表示按行堆叠。位置嵌入被添加到Z0以保留位置信息。令牌嵌入然后被输入到L={1,…L}层转换器,其输出被表示为ZL。在监督设置中,可学习的令牌 z [ C L S ] ∈ R d z^{[CLS]}∈R^d z[CLS]∈Rd作为 Z 0 : = ( z [ C L S ] : Z 0 ) ∈ R ( n + 1 ) × d Z_0:=(z^{[CLS]}:Z_0)∈R^{(n+1)×d} Z0:=(z[CLS]:Z0)∈R(n+1)×d附加到(1)中的令牌化图像。
**Transformer Layer **
变压器的每一层都由一个多头自关注(MSA)块和一个多层感知器(MLP)块组成。在MSA块中,对于 l ∈ L l∈L l∈L,输入 Z l − 1 ∈ R n × d Z_{l−1}∈R^{n×d} Zl−1∈Rn×d首先被投影到三个可学习嵌入 Q , K , V ∈ R n × d {Q,K,V}∈R^{n×d} Q,K,V∈Rn×d。注意力矩阵A计算如下
其中σ(.)表示行方向softmax操作。MSA中的“多头”是通过考虑h个注意头来定义的,其中每个头是 n × d / h n×d/h n×d/h矩阵的序列。使用线性层将注意力重新投射回n×d,该线性层与值矩阵组合为
MSA块的输出表示随后被输入到MLP块,该MLP块包括由GeLU激活分隔的两个线性层[24]。在给定的层l,通过变换器块的表示的计算流表示为
MSA和MLP块都具有与层归一化(LN)[3]的残余连接。虽然变换器的每一层中的MSA块都独立学习表示,但在下一小节中,我们表明,经验上这些层之间存在高度相关性。
3.2. Motivation: Layer Correlation Analysis
Attention-map correlation
ViT中的MSA块将每个补丁与每个其他补丁的相似性编码为n×n关注矩阵。该算子在 O ( n 2 ) O(n^2) O(n2)复杂度(2)的情况下计算开销较大。随着ViT规模的扩大,即随着n的增加,复杂性呈二次方增长,这一操作成为瓶颈。最近的NLP工作[51,52]表明,SoTA语言模型中相邻层之间的自我关注表现出非常高的相关性。这就提出了一个问题——在视觉变换器的每一层计算自我关注值吗?
为了解决这个问题,我们分析了ViT不同层的自我注意图的相关性。如图2所示,来自类标记A[CLS]的自我关注图表现出高度相关性,尤其是在中间层。 A l − 1 [ C L S ] A^{[CLS]}_{l−1} Al−1[CLS]和 A l [ C L S ] A^{[CLS]}_l Al[CLS]之间的余弦相似度可以高达0.97,如图2中每个注意力图的底部所示。我们在补充材料中分析了其他令牌嵌入的类似行为。我们通过计算每个 i , j ∈ L i,j∈L i,j∈L的 A i [ C L S ] A^{[CLS]}_i Ai[CLS]和 A j [ C L S ] A^{[CLS]}_j Aj[CLS]之间的中心核对齐(CKA)[12,27],定量分析ImageNet-1K的验证集的所有样本之间的这种相关性。从图3(a)中,我们观察到ViT-T在a[CLS]上具有高度相关性,尤其是从第3层到第10层。
Feature correlation
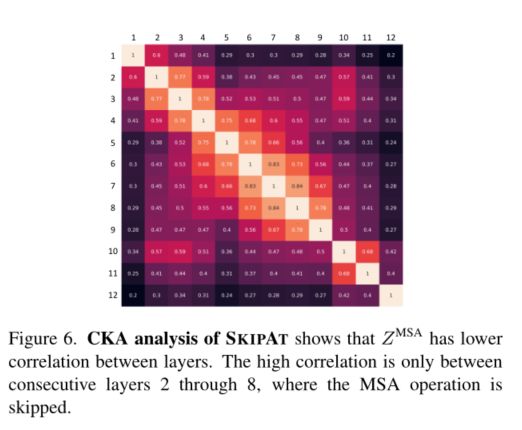
在ViT中,高相关性不仅限于A[CLS],MSA块的表示 Z M S A Z^{MSA} ZMSA也在整个模型中显示出高相关性[42]。为了分析这些表示之间的相似性,我们计算每个i,j∈L的 Z i M S A Z^{MSA}_i ZiMSA和 Z j M S A Z^{MSA}_j ZjMSA之间的CKA。我们从图3(b)中观察到, Z M S A Z^{MSA} ZMSA在模型的相邻层之间也具有高度相似性,尤其是在更早的层中,即从第2层到第8层。
3.3. Improving Efficiency by Skipping Attention
基于我们对变换器的MSA块之间的高表示相似性的观察(第3.2小节),我们建议利用注意力矩阵和MSA块中的表示之间的相关性来提高视觉变换器的效率。我们不是在每一层独立计算MSA操作(3),而是探索一种简单而有效的策略,以利用这些层的特性之间的依赖关系。
特别地,我们建议通过重用来自变压器的相邻层的表示来跳过变压器的一个或多个层中的MSA计算。我们将此操作称为“跳过注意”或“跳过”。由于跳过整个MSA块所带来的计算和内存益处大于仅跳过自我关注操作 ( O ( n 2 d + n d 2 ) v s . O ( n 2 d ) ) (O(n^2d+nd^2)vs.O(n^2d)) (O(n2d+nd2)vs.O(n2d)),因此在本文中,我们关注前者。然而,我们引入了参数函数,而不是直接重新使用特征,即将特征从源MSA块复制到一个或多个相邻MSA块。参数函数确保直接重用特征不会影响这些MSA块中的平移不变性和等变性,并作为一个强大的正则化器来改进模型泛化。
SKIPAT parametric function
设 Φ : R n × d → R n × d Φ:R^{n×d}→ R^{n×d} Φ:Rn×d→Rn×d表示将MSA块的输出从l−1映射到l的参数函数,其形式为: Z ^ l M S A : = Φ ( Z l − 1 M S A ) \hat{Z}_{l}^{\mathrm{MSA}}:=\Phi\left(Z_{l-1}^{\mathrm{MSA}}\right) Z^lMSA:=Φ(Zl−1MSA)这里, Z ^ l M S A \hat{Z}_{l}^{\mathrm{MSA}} Z^lMSA是ZMSAl的近似值。参数函数可以像身份函数一样简单,其中 Z l − 1 M S A Z_{l-1}^{\mathrm{MSA}} Zl−1MSA被直接重用。代替在l处计算MSA运算,我们使用 Z l − 1 M S A Z_{l-1}^{\mathrm{MSA}} Zl−1MSA作为在l处MLP块的输入。当使用同一函数时,由于在l处没有MSA运算,令牌之间的关系不再被编码在注意力矩阵中,这会影响表征学习。为了缓解这种情况,我们引入了受ResNeXt[62]启发的SKIPAT参数函数,如图4所示,以编码令牌之间的局部关系。SKIPAT参数函数由两个线性层和其间的深度卷积(DwC)[9]组成,如下所示:
在监督学习的情况下,我们首先将CLS嵌入从 Z M S A ∈ R ( n + 1 ) × d Z^{MSA}∈R^{(n+1)×d} ZMSA∈R(n+1)×d分离为类嵌入 Z C M S A ∈ R d Z^{MSA}_C∈R^d ZCMSA∈Rd和补丁嵌入 Z P M S A ∈ R n × d Z^{MSA}_P∈R^{n×d} ZPMSA∈Rn×d。然后将面片嵌入输入到第一线性层 F C 1 : R n × d → R n × 2 d FC_1:R^{n×d}→ R^{n×2d} FC1:Rn×d→Rn×2d,这扩展了通道尺寸。随后是 D w C : R √ n × √ n × 2 d → R √ n × √ n × 2 d DwC:R^{√n×√n×2d}→ R^{√n×√n×2d} DwC:R√n×√n×2d→R√n×√n×2d与内核R×R一起捕获交叉令牌关系。注意,在DwC操作之前,我们在空间上将输入矩阵重塑为特征张量。然后将DwC的输出变平为矢量,并馈送给最后一个FC层 F C 2 : R n × 2 d → R n × d FC_2:R^{n×2d}→ R^{n×d} FC2:Rn×2d→Rn×d,这将信道维度降低回其初始维度d。我们在FC1和DwC之后使用GeLU激活。在[53]之后,我们在FC2之后使用有效的信道注意模块(ECA)来增强跨信道依赖性。ECA模块首先使用全局平均池(GAP)沿信道维度聚合特征。应用1×1卷积,自适应核大小与信道维度成比例,然后进行sigmoid激活。ECA模块的这种操作增强了跨信道依赖性。然后,我们将类令牌的嵌入与ECA的输出连接起来,以获得 Z ^ l M S A \hat{Z}_{l}^{\mathrm{MSA}} Z^lMSA。
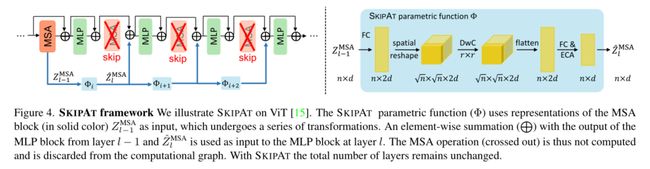
SKIPAT framework
SKIPAT的总体框架如图4所示。SKIPAT可以结合到我们在第4.4小节中经验显示的任何变压器架构中。根据体系结构,可以跳过变压器的一个或多个层中的MSA操作。在ViT中,由于我们根据经验观察到MSA块ZMSA的表示具有从第2层到第7层的高度相关性(第3.2小节),我们在这些层中使用SKIPAT参数函数。这意味着我们使用 Z 2 M S A Z^{MSA}_2 Z2MSA作为SKIPAT参数函数的输入,并跳过层3-8中的MSA操作。相反,SKIPAT参数函数输出的特征被用作MLP块的输入。表示的计算流程现在修改为
由于MSA和MLP块中存在残余连接(这是ViT[15]中的标准),第3层到第8层的MLP块独立学习表示,不能从计算图中丢弃。需要注意的是,使用SKIPAT,ViT中的总层数保持不变,但MSA块更少。
Complexity: MSA vs. SKIPAT
自我注意操作包括三个操作。首先,令牌嵌入被投影到查询、键和值嵌入中,其次,注意力矩阵A被计算为Q和K之间的点积,最后,输出表示被计算为A和V之间的点乘积。这导致了 O ( 4 n d 2 + n 2 d ) O(4nd^2+n^2d) O(4nd2+n2d)的复杂性。由于d≪n,MSA块的复杂度可以降低到 O ( n 2 d ) O(n^2d) O(n2d)。
SKIPAT参数函数由两个线性层和一个深度卷积运算组成,这导致 O ( 2 n d 2 + r 2 n d ) O(2nd^2+r^2nd) O(2nd2+r2nd)复杂度,其中r×r是DwC运算的内核大小。自 r 2 ≪ d r^2≪d r2≪d以来,SKIPAT的总体复杂性可以降低到 O ( n d 2 ) O(nd^2) O(nd2)。因此,当n随着变压器规模的增加而增加时,SKIPAT具有比MSA块更少的FLOP,因为 O ( n d 2 ) < O ( n 2 d ) O(nd^2)
4. Experiments
5. Conclusion
我们提出了SKIPAT,这是一个插件模块,可以放置在任何ViT架构中,以减少昂贵的SelfAttention计算。SKIPAT利用跨MSA块的依赖性,并通过重新使用先前MSA块的注意力来绕过注意力计算。为了确保隐喻共享是关怀的,我们引入了一个简单而轻的参数函数,该函数不会影响MSA中编码的归纳偏差。SKIPAT函数能够捕获交叉令牌关系,在吞吐量和FLOP方面计算速度更快的同时,性能优于基线。我们将SKIPAT插入到不同的变压器架构中,并在7个不同的任务中展示了其有效性。