【C++】15.AVL树

1.AVL树

• 它的左右子树都是AVL树
• 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)

#include 
using namespace std;

template
struct AVLTreeNode
{
    AVLTreeNode* _left;
    AVLTreeNode* _right;
    AVLTreeNode* _parent;//为什么三叉链 跟平衡因子有关

    int _bf; // balance factor 平衡因子

    pair _kv;//值

    AVLTreeNode(const pair& kv)
        :_left(nullptr)
        ,_right(nullptr)
        ,_parent(nullptr)
        ,_kv(kv)
        ,_bf(0)
    {}
};

2.AVL树的插入

分成两步:

1. 按照二叉搜索树的方式插入新节点
2. 调整节点的平衡因子

第一步已经在上篇博客实现 难度在第二步

平衡因子会有三种变化 插入后:

• parent->_bf=0
• parent->_bf=1/-1
• parent->_bf=2/-2

还会涉及到parent上面的祖先需不需要变化 我们一步步来

bf=1/-1 bf=0的情况:

bf=2/-2的情况:

非常复杂 需要进行旋转

bool Insert(const pair& kv)
{
    if (_root == nullptr)
    {
        _root = new Node(kv);
        _root->_bf = 0;
        return true;
    }

    Node* parent = nullptr;
    Node* cur = _root;

    while (cur)
    {
        if (cur->_kv.first > kv.first)
        {
            parent = cur;
            cur = cur->_left;
        }
        else if (cur->_kv.first < kv.first)
        {
            parent = cur;
            cur = cur->_right;
        }
        else
        {
            return false;
        }
    }

    cur = new Node(kv);
    if (parent->_kv.first < kv.first)
    {
        parent->_right = cur;
        cur->_parent = parent;
    }
    else
    {
        parent->_left = cur;
        cur->_parent = parent;
    }

    //2.更新平衡因子
    while (parent)
    {
        //更新parent的平衡因子
        if (cur == parent->_right)
            parent->_bf++;
        else
            parent->_bf--;

        //判断parent上面的祖先还需不需要调整
        if (parent->_bf == 0)
        {
            //说明parent所在的子树的高度不变 更新结束
            break;
        }
        else if (parent->_bf == 1 || parent->_bf == -1)
        {
            //说明parent所在的子树的高度变了 继续往上更新
            cur = parent;
            parent = parent->_parent;
        }
        else if (parent->_bf == 2 || parent->_bf == -2)
        {
            //parent所在的子树出现不平衡了 需要旋转处理
            //出现不平衡 需要旋转处理
            //1.旋转完成后 还得是搜索树
            //2.旋转完成后 还得是平衡
            //旋转步骤
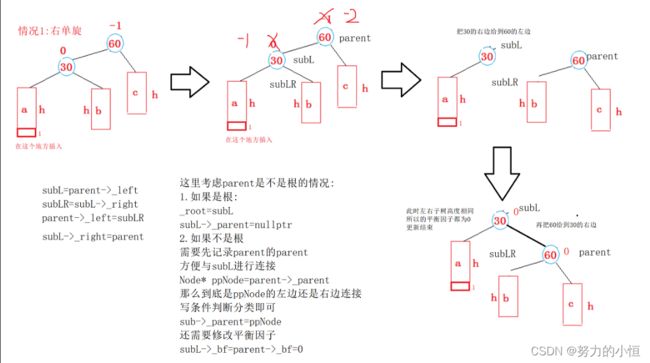
            //左单旋
            //1.subR的左边给parent的右边
            //2.parent变成subR的左边
            //subR的parent比subR小
            //subR变成了树的根
            if (parent->_bf == 2)
            {
                if (cur->_bf == 1)
                {
                    //说明右边高 走左旋
                    RotateL(parent);
                }
                else if (cur->_bf == -1)
                {
                    RotateRL(parent);//右左双旋
                }
            }
            else if (parent->_bf == -2)
            {
                if (cur->_bf == -1)
                {
                    //说明左边高 走右旋
                    RotateR(parent);

                }
                else if (cur->_bf == 1)
                {
                    RotateLR(parent);//左右双旋
                }
            }
        }
        //旋转完成后 parent所在的树的高度恢复到了 插入结点前高度
        //如果是子树 对上层影响 更新结束
        break;
    }
    return true;
}

//左单旋
void RotateL(Node* parent)
{
    Node* subR = parent->_right;

    //parent->_right = subR->_left;
    //subR->_left = parent;
    没有处理每个结点的parent 不行

    //需要处理subR的parent left
    //需要处理subRL的parent
    //需要处理parent的right parent
    Node* subRL = subR->_left;
    parent->_right = subRL;
    if (subRL)//subRL为空 不用改 不为空 连接subRL和parent
        subRL->_parent = parent;

    subR->_left = parent;
    //parent的parent就是ppNode 保存
    Node* ppNode = parent->_parent;
    parent->_parent = subR;//连接parent和subR

    //此时subR的parent还没有处理
    //这里又分两种情况
    //1.原来parent是这颗树的根 现在subR是根
    if (_root == parent)
    {
        _root = subR;
        subR->_parent = nullptr;
    }
    //2.原来parent不是这颗树的根 
    //找到parent的上一个ppNode与subR进行连接
    //这里又有ppNode的left/right subR的parent需要处理
    else
    {
        //subR顶替parent的位置
        if (ppNode->_left == parent)
            ppNode->_left = subR;
        else
            ppNode->_right = subR;

        subR->_parent = ppNode;
    }

    //还要考虑平衡因子
    parent->_bf = subR->_bf = 0;
}

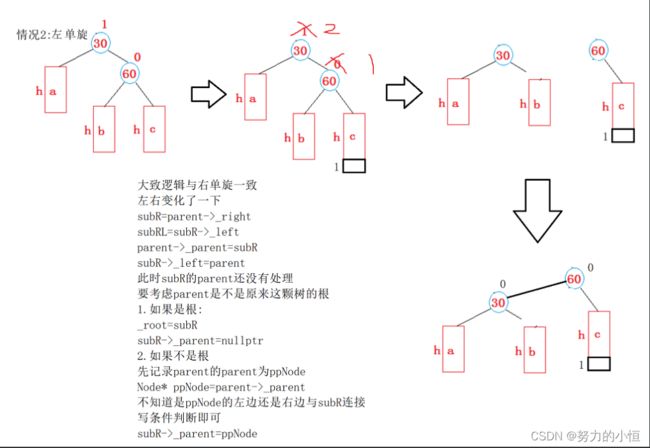
//右单旋 与左单旋逻辑一样
void RotateR(Node* parent)
{
    Node* subL = parent->_left;
    Node* subLR = subL->_right;

    parent->_left = subLR;
    if (subLR)
        subLR->_parent = parent;

    subL->_right = parent;
    Node* ppNode = parent->_parent;
    parent->_parent = subL;

    if (_root == parent)
    {
        _root = subL;
        subL->_parent = nullptr;
    }
    else
    {
        if (ppNode->_left == parent)
            ppNode->_left = subL;
        else
            ppNode->_right = subL;

        subL->_parent = ppNode;
    }
    subL->_bf = parent->_bf = 0;
}

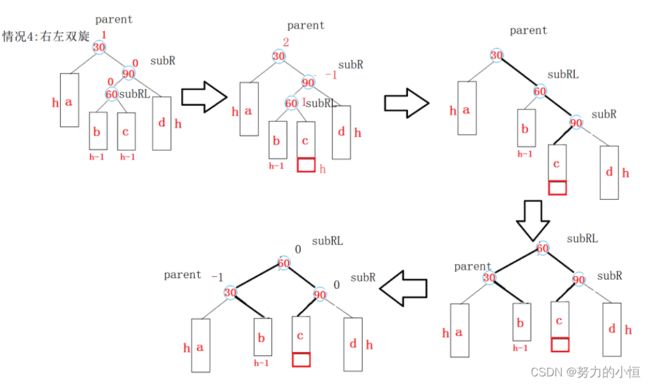
//左右双旋(先左旋再右旋)
//右左双旋
void RotateRL(Node* parent)
{
    Node* subR = parent->_right;
    Node* subRL = subR->_left;
    int bf = subRL->_bf;//通过subRL的平衡因子来判断后续情况

    RotateR(parent->_right);//右旋转
    RotateL(parent);//左旋转

    //对应图来理解
    if (bf == -1)//在b插入
    {
        parent->_bf = 0;
        subR->_bf = 1;
        subRL->_bf = 0;
    }
    else if (bf == 1)//在c插入
    {
        parent->_bf = -1;
        subR->_bf = 0;
        subRL->_bf = 0;
    }
    else if (bf == 0)//bc都没有
    {
        parent->_bf = 0;
        subR->_bf = 0;
        subRL->_bf = 0;
    }
}
//边上插入 祖先平衡因子的改变是一条直线 单旋即可
//中间插入 祖先平衡因子的改变是一条折线 双旋即可

void RotateLR(Node* parent)
{
    Node* subL = parent->_left;
    Node* subLR = subL->_right;
    int bf = subLR->_bf;

    RotateL(subL);
    RotateL(parent);

    if (bf == 1)
    {
        parent->_bf = 0;
        subL->_bf = -1;
        subLR->_bf = 0;
    }
    else if (bf == -1)
    {
        parent->_bf = 1;
        subL->_bf = 0;
        subLR->_bf = 0;
    }
    else if (bf == 0)
    {
        parent->_bf = 0;
        subL->_bf = 0;
        subLR->_bf = 0;
    }
}

//判断旋转类型
//左子树较高 插入子树左侧->左单旋 插入子树右侧->左右双旋
//右子树较高 插入子树右侧->右单旋 插入子树左侧->右左双旋

void _InOrder(Node* root)
{
    if (root == nullptr)
        return;

    _InOrder(root->_left);//递归左树
    cout << root->_kv.first << ":" << root->_kv.second << " " << endl;
    _InOrder(root->_right);//再递归右树
}

//隐含的this指针 root传不了 写一个_InOrder
void InOrder()
{
    _InOrder(_root);
    cout << endl;
}

int Height(Node* root)
{
    if (root == nullptr)
        return 0;

    int leftHeight = Height(root->_left);
    int rightHeight = Height(root->_right);
    
    return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

bool IsBalance()
{
    return _IsBalanceTree(_root);
}

bool _IsBalanceTree(Node* root)
{
    //空树也是AVL树
    if (nullptr == root)
        return true;

    int leftHeight = Height(root->_left);
    int rightHeight = Height(root->_right);

    return abs(leftHeight - rightHeight) < 2
        && _IsBalanceTree(root->_left)
        && _IsBalanceTree(root->_right);
}

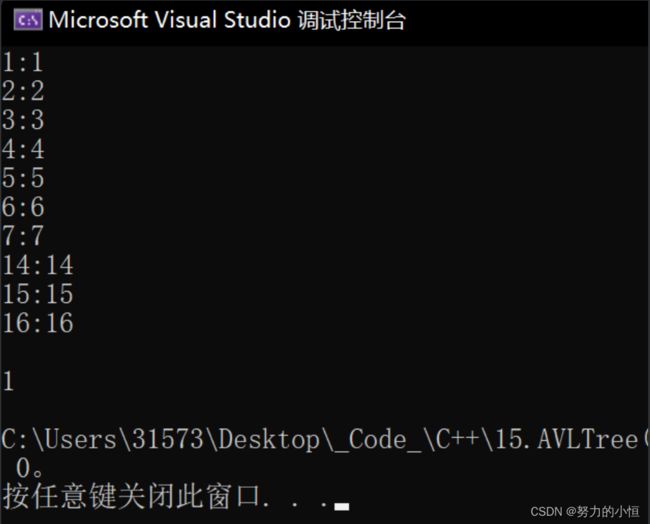
3.测试

void TestAVLTree()
{
    //int a[] = { 16,3,7,11,9,26,18,14,15 };
    int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
    AVLTree t;
    for (auto e : a)
    {
        t.Insert(make_pair(e, e));
    }

    t.InOrder();

    cout << t.IsBalance() << endl;
}

 

【C++】15.AVL树 完