蓝桥杯倒计时 | 倒计时6天

作者️‍♂️：让机器理解语言か

专栏：蓝桥杯倒计时冲刺

描述：蓝桥杯冲刺阶段，一定要沉住气，一步一个脚印，胜利就在前方！

寄语：没有白走的路，每一步都算数！

题目：小朋友崇拜圈（2018年省赛）

题目描述

班里 N 个小朋友，每个人都有自己最崇拜的一个小朋友（也可以是自己）。

在一个游戏中，需要小朋友坐一个圈，每个小朋友都有自己最崇拜的小朋友在他的右手边。

求满足条件的圈最大多少人？

小朋友编号为 1,2,3,⋯N。

输入描述

输入第一行，一个整数 N（3

接下来一行 N 个整数，由空格分开。

输出描述

要求输出一个整数，表示满足条件的最大圈的人数。

输入输出样例

输入

9
3 4 2 5 3 8 4 6 9

输出

4

样例解释

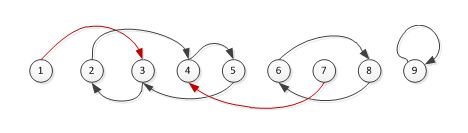
如下图所示，崇拜关系用箭头表示，红色表示不在圈中。

显然，最大圈是[2 4 5 3] 构成的圈。

题解1：

        本题最大的难点在于理解题目，按照题目描述，很容易理解成x崇拜的人位于x的右边，也就是这组整数相邻的人构成崇拜关系，然而结合图形和输入的N个整数，发现如果将这些整数看成是一个数组nums，那么构成崇拜关系的规律应该是x崇拜nums[x-1]，那么问题也就迎刃而解了。 

代码：（57.1%） 

n = int(input())
nums = [0] + list(map(int,input().split()))

max_ = 0
for i in range(1,len(nums)):
  con = 0
  lst = []
  x = nums[i]
  while x not in lst:
    lst.append(x)
    x = nums[x]
    con += 1
    if con > max_:
      max_ = con

print(max_)

题解二：

用DFS搜索寻找最大的圈 

用vis存储崇拜者顺序，vis[i]的值代表当前圈内的人数。vis[1]中的下标‘1’表示圈内第一个小朋友崇拜的对象所在的位置 ，vis[2]中的下标‘2’表示第二个小朋友崇拜的对象所在的位置 ，以此类推。

圈中的人数 = 当前列表长度i - 已经在vis中的那个小朋友的下标

样例中vis的全部情况：
第一次DFS：[0, 0, 2, 1, 3, 4, 0, 0, 0, 0]

第二次DFS：[0, 0, 2, 1, 3, 4, 2, 0, 1, 0]
第三次DFS：[0, 0, 2, 1, 3, 4, 2, 0, 1, 0]
第四次DFS：[0, 0, 2, 1, 3, 4, 2, 0, 1, 1]

在第一次DFS中，递归到第5次时f[u]=3（第五个小朋友的崇拜者是3），vis[f[u]]=1，出现了列表vis中存在的数字，表示已经闭环了。当前列表长度为5，减去已经存在vis中的小朋友下标vis[3]=1，就是当前圈内的人数4。

 代码： （AC）

# 也可以用图，进行计算
'''
1、构造一个关系矩阵
2、从第一个开始遍历，到最后可以放回原点，则存储到列表
3、
注：
  如果遍历过程中回到之前的点，则截至
'''

import sys
sys.setrecursionlimit(1000000)
n=int(input())
f=[0]+list(map(int,input().split()))
vis=[0]*(n+1)#存储崇拜者顺序
ans=0

def dfs(u,i):
    if vis[u]:        #vis[u]访问过，成环了
        global ans
        ans=max(ans,i-vis[u])# 圈的人数 = 当前列表长度i - 已经在vis中的那个小朋友的下标
        return
    vis[u]=i#
    dfs(f[u],i+1)#f[u]:寻找下一个崇拜者  i+1:当前构成环的长度+1

for i in range(1,n+1):
    if not vis[i]:        # 没有访问过的
      dfs(f[i],1)            #从i开始遍历，环默认为1
      # print(vis)
# vis的全部情况
# [0, 0, 2, 1, 3, 4, 0, 0, 0, 0]
# [0, 0, 2, 1, 3, 4, 2, 0, 1, 0]
# [0, 0, 2, 1, 3, 4, 2, 0, 1, 0]
# [0, 0, 2, 1, 3, 4, 2, 0, 1, 1]
print(ans)