数据库查询语言的进化（下）

UQL(Ultipa图查询语言)如何在图上实现查询功能？

1. 从某个顶点出发，找到它的第1到第K层（跳）的所有邻居并返回

UQL=Ultipa Query Language，是与Ultipa Graph高并发实时图数据库匹配的查询语言。

除了明显的性能优势外，UQL的另外一个重要特点是高易用性、易掌握，并有贴近自然语言的易读性。UQL可以通过Ultipa Manager、Ultipa CLI或Ultipa SDK/API的接口调用。此外，实现上面的查询，在UQL中只需要1句话即可完成。

一句话uQL:

spread().src(123).depth(6).spread_type(“BFS”).limit(4000);

上面的语句简单易懂，基本上不需要太多解释，调用spread()函数，从顶点123出发，搜索深度为6层，以BFS的方式进行搜索，限定返回最多4000个顶点（以及关联的边）。在上图中，红色的小点就是起始顶点，通过以上语句操作的全部返回的顶点和边所形成的子图就直接显示在Ultipa Graph的WEB界面上了。

事实上，spread()这个操作相当于允许从任何顶点出发找到它的联通子图 ，或者说它的邻居网络的形态可以被直接计算出来，并通过可视化界面直观展示出来。用这种方式也可以看出生成的联通子图中的顶点和边所构成的热点、聚集区域等图上的空间特征 ,而并不需要传统数据库中的 E-R模型图。

2. 给定的多个顶点，自动组网（形成一张顶点间相互联通的网络）

本查询相对于熟悉传统数据库的读者来说或许就显得过于复杂了，用SQL也许无法实现这个组网功能。但是，对于人的大脑而言，这是个很天然的诉求——当你想在张三、李四、王五和赵六之间组成一张关联关系的网络的时候，你已经开始在脑海里绘制下面这张图了。

很显然，uQL倾向于继续使用1句话来实现这个“不可能”的操作：

autoNet().addSrcs(12,21,30,40,123).depth(4).limit(5)
autoNet()就是我们调用的主要函数，它的名字已经非常直白了 ——自组网操作。你只需要提供一组顶点的ID信息，组网搜索的深度（4层=4跳），任意两个顶点间的路径数量限制（5）。

下面，我们从纯数学的角度来分析一下，这个组网操作的计算复杂度：

可能返回路径数量： C(5, 2) * 5 = (5 * 4 / 2) * 5 = 50 条
预估图上计算复杂度： 50 paths *(E/V)4 = 50 * 256 = 12800

注：我们假设图中的(边数/顶点数)比例=4（平均值），也就是E/V=4，搜索深度为4的时候每条路径需要平均计算256（4**4）次。

这个查询在现实世界的应用中意义非同凡响。例如执法机关会根据电话公司的通话记录来跟踪多名嫌疑人的通话所组成的深度网络的特征来判断是否有其它嫌疑人牵连其间，犯罪集团是否存在某种异动，或者任意个数的嫌疑人构成的犯罪组织（crime ring）间的微妙的联动关系等。

传统大数据技术框架之上，这种多节点的组网操作极为复杂，甚至是没有可能完成的任务。

原因是因为计算复杂度太高 ，对于计算资源的需求太高，在短时间内没有可能完成，或者是以T+7（亦或T+15、T+30）的方式实现，等到结果出来的时候，嫌疑人早已逃之夭夭或者罪案已发生良久了。

假设有1000个嫌疑人需要参与组网，他们之间形成的网络的路径至少有 50万条(1,000 * 999) / 2）。如果查询路径深度为6层，如上所述，这个计算复杂度是20亿次（假设E/V=4,实际上E/V可能>=10，那么计算次数可能达到50万亿次）。

基于Spark架构的计算平台可能需要数天来完成运算；
利用Ultipa Graph，该操作是以实时到近实时（T+0）的方式完成的。

Ultipa Graph在不同的数据集上做过性能评测，Ultipa的性能至少是Spark框架的几百倍到数千倍 。 如果原来需要Spark系统1天完成的计算，Ultipa仅需数秒、数分钟！当与罪案斗争的时候，每一秒都很宝贵。

值得一提的是，作为实时高并发图数据库，Ultipa Graph在性能第一的前提下，还开发了集简洁、直观、易懂于一体的UQL语言(Ultipa查询语言)——只要掌握了最基本的语法规则后，只需20分钟，就能让一名普通人开始上手使用Ultipa图系统。

UQL借鉴并采用了锁链式查询（chain-query）的语言风格，对于熟悉文档型数据库MongoDB的读者而言，上手UQL就更加简单了。例如，一个简单的链式路径（点到点）查询语句：

上面的例子中是去查询两个顶点间深度为5度的路径，限定返回5条路径，并且返回匹配的属性“name”(通常是顶点或边的名称属性)。

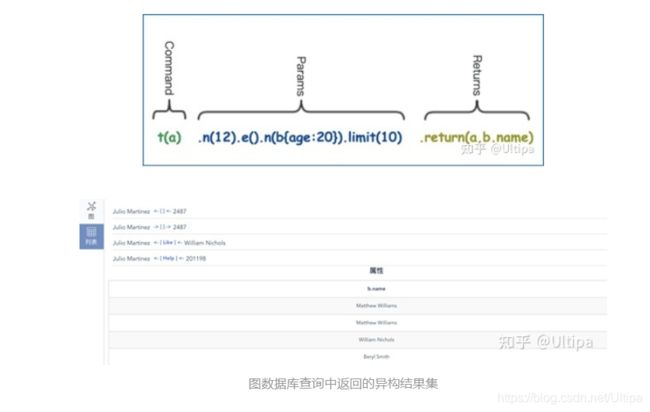
我们再来看一个稍微复杂一点的例子，模板查询，当然，它所完成的功能也更加的强大。例如下面的例子中t()代表调用模板查询调用，t(a)表达的是为当前模板设定一个别名为a，从顶点12开始，经过一条边抵达到属性age值为20的顶点b（别名），返回这个模板所匹配的结果a和抵达顶点b的名字。和传统SQL类似的地方是可以对任何过滤条件设置别名，和SQL不同的地方是，当异构的结果a和b.name一同被返回的时候，a表达的是整个模板搜索所对应的路径结果的集合，而b.name则是一组顶点的属性的数组集合（如下图所示）。这种异构灵活性是SQL不具备的。

下面我们再用一个例子来说明在图查询中使用简单的查询语言实现深度的、递归式的查询：

t(a1).n(n1{age:20}).e(e1{rank:{$bt:[20,30]}})[3:7].n(n2).limit(50).
return(a1, n1, e1, n2._id, n2.name)

这个语句中，从年龄=20岁的顶点（可能有多个）出发，进行深度为3-7层的路径搜索查询抵达某些顶点，并且路径中每条边的权重介于20-30之间，找到50条路径，并返一系列异构的数据（模板匹配的路径本身、起始顶点、边、终止顶点的两个属性）。这种灵活度在SQL当中，如果不通过书写大量的封装代码是很难实现的，而且这种搜索深度也是令关系型数据库望而却步的——通常会发生因内存或系统资源耗尽而导致数据库出现SEG-FAULT。

3.数学统计类型的查询，例如count(),sum(), min(), collect()等

这个例子对于SQL编程爱好者而言一点都不陌生 ——统计一家公司员工的工资总和。

t§.n(12).le({type:“works_for”}).n(c{type:“human”}).return(sum(c.salary))

在UQL中实现也是一句话的事情：

· 从公司顶点12出发
· 找到所有工作于（边关系）本公司的员工，别名为c
· 返回他们全部工资之和

在一张小表中，这个操作在SQL语境下同样毫无压力，但是在一张大表中（千万或亿万行），或许这个SQL操作就会因为表扫描而变得缓慢了。而在Ultipa数据库中因为采用相邻哈希+近邻存储的存储逻辑及并发逻辑优化，这种面向一步抵达的邻居顶点的数学统计操作几乎不会受到数据集大小的影响，进而可以让任务执行时间基本恒定！

下面这个例子中，则是统计该公司的员工都来自于哪几个省:

t§.n(12).e({type:“works_for”}).n(c{type:“employee”}).
return(collect(c.province))

上面的两个例子是来说明通过uQL的方式同样可以实现传统关系型SQL查询所能实现的功能。同样，返回结果也可以以关系型数据库查询结果所常用的表单、表格的方式来呈现，例如下面的两图所示：

在Ultipa Manager中以表格的方式展示结果列表
上图中，khop()操作返回的是从初始顶点出发经过depth()限定的深度搜索后返回的第K层的邻居的集合，select()的使用允许你选定需要具体返回的属性。

下图中展示的是类似的操作在Ultipa CLI中返回的结果示例。注意下图中的时间有两个维度，引擎时间和全部时间，其中引擎时间是内存图计算引擎的运算耗费时间，而全部时间还包括一些持久化存储层的数据转换的时间。

4. 强大的基于模板的全文搜索

如果一个数据库系统中不能支持全文搜索，那么我们很难能称其为完整的数据库。在图数据库支持全文搜索并不是一个全新的事情，例如老牌的图数据库Neo4j中通过集成Apache Lucene的全文搜索框架，让用户可以通过Cypher语句来对顶点（及其属性）进行全文本搜索。在Ultipa Graph中我们并没有采用开源的Apache Lucene/Solr，其中一个很重要的原因是性能落差，在我们看来Lucene/Solr的架构的性能要指数级的低于Ultipa的核心计算引擎（另外一个次要的原因是这种开源的框架中依然存在着不可预知的一些问题，在生产环境中一旦暴露，修复起来非常困难，这个或许可被看做是开源的一个重大迷思）。

在uQL中完成面向顶点的全文搜索，只需要下面这句简单的查询语句：

find().nodes(~name:“Sequoia*”).limit(100).select(name,intro)

这句uQL返回的是找到100个包含“红杉”字样的顶点，并返回它们的name和intro属性。这个查询非常类似于传统数据库中的面向某张表的列信息查询。同样的，也可以针对边来进行查询，例如下面：

find().edges(~name:“Love*”).limit(200).select(*)

找到图中所有的边上的name属性中存在“爱情“字样的关系。

当然，如果我们的全文检索只是停留在点、边查询，那么这就略显单薄了。在Ultipa图数据库中，其创造性的发明了基于模板匹配的全文本查询 。例如，模糊的搜索从“红杉”出发到“招银”的一张关联关系网络，网络中的路径搜索深度不超过5层，返回20条路径所构成的子图。注意：这个搜索时从模糊匹配顶点出发，到达模糊匹配的另外一套顶点！

t().n(~name: “Sequoia*”).e()[:5].n(~name: CMB*").limit(20).select(name)

如果不用上面这句简单得不能再简单的uQL，你能想象如何用其它SQL或NoSQL语言来实现吗？假设我们在一个工商数据集之上，在天眼查、企查查做类似的查询，你要先找到名字中包含有红杉或招银字样的公司，然后再分别对每一家公司的投资关系进行梳理，你需要查清楚每家被投公司的合作、竞争、董监高等关系，然后再慢慢梳理出来是否能在5步之内关联上名称中包含红杉字样的一家公司和包含招银字样的另一家公司。这个操作绝对的是让人疯狂的，你可能需要花费数天的时间来完成，或者能够通过写代码调用API的方式来“智能”化的实现。无论如何，你很难在下面两件事情上击败UQL:

· 效率和时延（Efficiency and Latency）：一言以蔽之实时性！ · 准确率和直观度（Efficacy and
Accuracy）:直观、易读、易懂
在上图中，这个看起来简单而又实际上非常复杂的查询操作仅仅耗时50ms！这种复杂查询的效率性是前所未有的。

一门先进的（数据库）查询语言的优美感，不是通过它到底有多复杂，而是通过它有多简洁来体现的。它应该具备这样的一些通性：

· 易学、易懂（Easy to Learn，Easy to Understand） · 高性能（Lightning
Fast）：当然，其实这个其实取决于底层的数据库引擎！
· 系统的底层复杂性不应该暴露到语言接口层面（System Complexity Shielded-Off）

特别是上文的最后一点，如果读者对于SQL或Gremlin或Cypher或GraphSQL当中复杂的嵌套逻辑心有余悸的话，你会更理解下面的这个比喻：当古希腊神话中的泰坦Atlas把整个世界（地球）抗在他的肩膀上的时候，世界公民们（数据库用户）并不需要去感知这个世界有多沉重（数据库有多复杂）。

5. 复杂的图算法

区别于其他数据库，图数据库的优势之一是集成化的算法功能支持。图上有很多种算法，例如出入度、中心度、排序、传播、连接度、社区识别、图嵌入、图神经元网络等等。随着商用场景的增多，相信会有更多的算法被移植到图上或者被发明创造出来。

以鲁汶社区识别算法为例，这个算法出现的时间仅仅十几年，它得名于它的诞生地——比利时法语区的鲁汶大学（Louvain University）。它发明的初衷是用来通过复杂的多次递归遍历一张由社交关系属性构成的大图中的点、边来找到所有的顶点（例如人、事、物）所构成的关联关系社区，紧密关联的顶点会处于同一社区，不同的顶点可能会处于不同的社区。在互联网、金融科技领域，鲁汶算法受到了相当的重视。下面这行uQL语句完成了鲁汶算法的调用执行：

algo().louvain({phase1_loop:5, min_modularity_increase:0.01})
在图数据库中，调用一个算法与执行一个API调用是比较类似的，都需要提供一些必须的参数。上例中，用户仅需提供最少两个参数就可以执行鲁汶。当然，可选的，用户可以设定更为复杂的参数集来优化鲁汶算法，因篇幅所限，本文不展开描述，若对此感兴趣的读者可关注Ultipa官网。

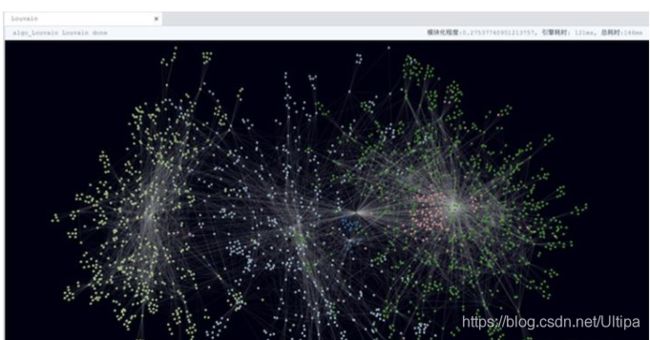
注：原生的鲁汶社区识别算法的实现是串行的，也就是说它需要从全图中的所有顶点出发，逐个顶点、逐条边的去进行反复的运算。试想在一张大图中（千万顶点以上），这个计算的时间复杂度绝对的是要以T+1来衡量的。例如在Python的NetworkX库中，对一个普通的（几十万-几百万顶点）图数据集进行鲁汶运算要耗时数个、数十个小时，但是在Ultipa Graph上面这个计算的耗时通过高度的并发被剧烈的缩短到了毫秒、秒级！在这里，我们探讨的不是10倍—100倍的性能超越，而是成千上万倍的性能提升！如果读者觉得我们给出的案例只是天方夜谭或是痴人说梦，或许你应当重新审视一下你对于数据结构、算法以及它们的最优工程实现的理解了。

UQL图查询语言中还支持很多功能强大的操作，上面的5个例子只是起到了一个抛砖引玉的作用，笔者希望它们能揭示UQL的简洁性，并唤起读者去思考一个问题：你到底是愿意去绞尽脑汁的书写成百上千行的SQL代码，并借此杀死你我他的大量脑细胞来读懂你的代码呢？还是考虑用更简洁、方便却更加强大的图语言呢？

关于数据库查询语言，Ultipa认为：

· 数据库查询语言不应该只是数据科学家、分析员的专有工具，任何业务人员都可以（并应该）掌握的一门查询语言。 ·
查询语言应当便于使用，所有数据库底层的架构、工程实现的复杂性应当对于上层的用户而言是透明的！
·介于图数据库的巨大潜力，在未来的一段时间内会大幅的替代SQL的负载，有一些业界顶级的公司，例如微软和亚马逊已经预估未来8-10年间，会有40-50%的SQL负载会迁移到图数据库之上完成。让我们拭目以待。

有些人认为，包括一些知名的投资机构和行业“专家”，关系型数据库和SQL永远也不会被取代。我们发现这种看法禁不起推敲。如果我们稍微回顾一下不是很久远的历史就会发现，关系型数据库在70—80年代取代了导航型数据库，它已经称霸了行业40—50年了，如果历史真正教会我们任何东西，那就是对于任何事情的执着和痴迷都不会长久，特别是在这个互联网科技的时代。

最后，用笔者喜欢的一段话送给诸位读者：

“What you cherish, perish”

“What you resist, persist”

你珍爱的，终将消亡

你抵抗的，必将永存。

·END·