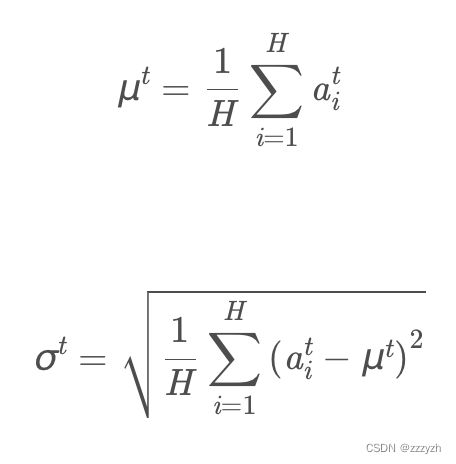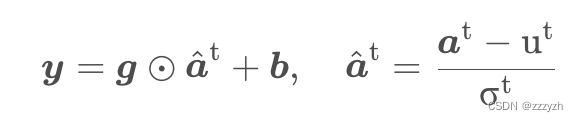CV【5】:Layer normalization
系列文章目录
Normalization 系列方法(一):CV【4】:Batch normalization
Normalization 系列方法(二):CV【5】:Layer normalization
文章目录
- 系列文章目录
- 前言
- 2. Layer normalization
-
- 2.1. Motivation
- 2.2. Method
-
- 2.2.1. Standardisation
- 2.2.2. Calculation preparation
- 2.2.3. Calculation process
- 2.3. Implement with PyTorch
- 总结
前言
对于早前的 CNN 模型来说,大多使用 batch normalization 进行归一化,随着 Transformer 在计算机视觉领域掀起的热潮, layer normalization 开始被用于提升传统的 CNN 的性能,在许多工作中展现了不错的提升
本文主要是对 layer normalization 用法的总结
2. Layer normalization
2.1. Motivation
Batch Normalization 使用 mini-batch 的均值和标准差对深度神经网络的隐藏层输入进行标准化,可有效地提升训练速度
BN 的效果受制于 batch 的大小,小 batch 未必能取得预期效果
- 对于前向神经网络可以很直接地应用
BN,因为其每一层具有固定的神经元数量,可直接地存储每层网络各神经元的均值、方差统计信息以应用于模型预测 - 在
RNNs网络中,不同的 mini-batch 可能具有不同的输入序列长度(深度),比如每句话的长短都不一定相同,所有很难去使用BN,计算统计信息比较困难,而且测试序列长度不能大于最大训练序列长度
Barch Normalization 也很难应用于在线学习模型,以及小 mini-batch 的分布式模型
Layer Normalization 是针对自然语言处理领域提出的,其计算是针对每个样本进行的, 不像 BN 那样依赖 batch 内所有样本的统计量, 可以更好地用到 RNN 和流式数据上(注意,在图像处理领域中 BN 比 LN 是更有效的,但现在很多人将自然语言领域的模型用来处理图像,比如 Vision Transformer,此时还是会涉及到 LN,有关 Vision Transformer 的部分可以参考我的另外一篇 blog:CV-Model【6】:Vision Transformer)
2.2. Method
2.2.1. Standardisation
网络层的输出经过线性变换作为下层网络的输入,网络输出直接影响下层网络输入分布,这是一种协变量转移的现象。我们可以通过 固定网络层的输入分布(固定输入的均值和方差) 来降低协变量转移的影响
BN 对同一 mini-batch 中对不同特征进行标准化(纵向规范化:每一个特征都有自己的分布),受限于 batch size,难以处理动态神经网络中的变长序列的 mini-bach
RNNs 不同时间步共享权重参数,使得 RNNs 可以处理不同长度的序列,RNNs 使用 layer normalization 对不同时间步进行标准化(横向标准化:每一个时间步都有自己的分布),从而可以处理单一样本、变长序列,而且训练和测试处理方式一致
2.2.2. Calculation preparation
LN 是基于 BN 转化而来的
对于一个多层前向神经网络中的某一层 H i H_i Hi,计算方式如下所示:
a i l = w i l T h l h i l + 1 = f ( a i l + b i l ) a_i^l = w_i^{l^T}h^l \\ h_i^{l+1} = f(a_i^l + b_i^l) ail=wilThlhil+1=f(ail+bil)
针对深度学习,存在 covariate shift 现象,因此需要通过 normalize 操作,使 H i H_i Hi 层的输入拥有固定的均值和方差,以此削弱协方差偏移现象对深度网络的训练时的影响,加快网络收敛。
normalize 对 H i H_i Hi 层输入进行变换,计算方式如下所示:
a ˉ i l = g i l σ i l ( a i l − μ i l ) μ i l = E x ∼ P ( x ) [ a i l ] σ i l = 1 H ∑ i = 1 H ( a i l − μ l ) 2 \bar{a}_i^l = \frac{g_i^l}{\sigma_i^l}(a_i^l - \mu_i^l) \\ \mu_i^l = \mathbb{E}_{x \sim P(x)} [a_i^l] \\ \sigma_i^l = \sqrt{\frac{1}{H} \displaystyle\sum_{i=1}^H (a_i^l - \mu^l)^2} aˉil=σilgil(ail−μil)μil=Ex∼P(x)[ail]σil=H1i=1∑H(ail−μl)2
直接使用上式进行 normalize 不现实,因为需要针对整个 trainingset 来进行计算,因此,BN 通过 mini-batch 的输入样本近似的计算 normalize 中的均值和方差,因此成为 batch normalization
2.2.3. Calculation process
与 BN 不同,LN 是针对深度网络的某一层的所有神经元的输入按以下公式进行 normalize 操作
如图所示。它综合考虑一层所有维度的输入,计算该层的平均输入值和输入方差,然后用同一个规范化操作来转换各个维度的输入
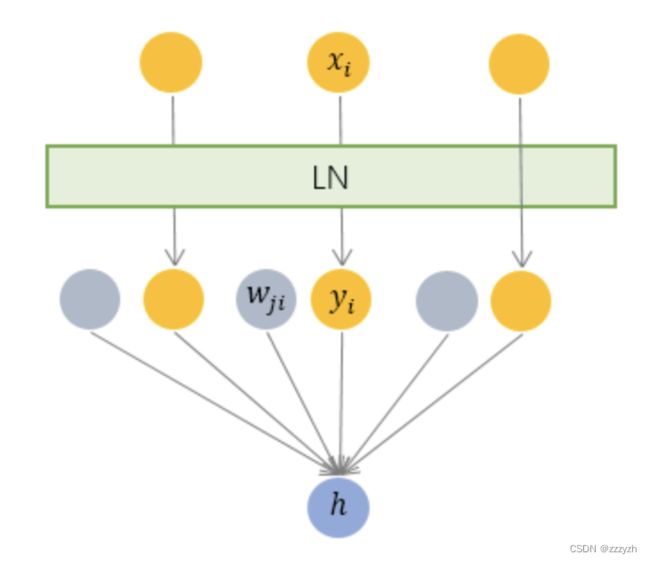
对于 RNN 的每个时间步,其输入都会包含两部分,即当前的输入 x t x^{t} xt 和上一个时刻的隐藏状态 h t − 1 \mathbf{h}^{t-1} ht−1,记 a t = W h h h t − 1 + W x h x t \mathbf{a}^{t}=W_{h h} h^{t-1}+W_{x h} \mathbf{x}^{t} at=Whhht−1+Wxhxt,其中, W h h W_{hh} Whh 和 W x h W_{x h} Wxh 为对应的权重矩阵,则在每一个时刻,Layer Normalization 对每一个样本都分别计算所有神经元的均值和标准差如下:
- a t \mathbf{a}^{t} at 表示输入向量(前层网络输出加权后的向量)
- H H H 表示隐藏单元数量(
RNN层的维度)
对于标准 RNN,若当前输入为 x t \mathbf{x}^{t} xt,上一隐藏状态为 h t − 1 \mathbf{h}^{t-1} ht−1,则加权输入向量(非线性单元的输入)为:
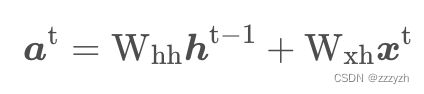
对输入向量进行层标准化,再进行缩放和平移(用于恢复非线性)得标准化后的输入 y \mathbf{y} y:
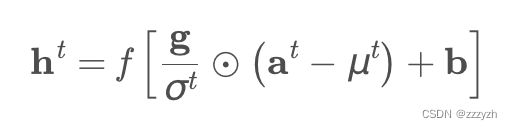
其中, g g g 和 b b b 为引入的自适应增益和偏置参数,其作用与 batch normalization 中的参数一样,为了保留模型的非线性能力, g g g 和 b b b 的维度均为 H H H
值得注意的是,在每个时间步,同层网络的所有隐藏单元共享均值和方差
Layer Normalization 对 g g g 和 b b b 的初始化不敏感,一般默认将 g g g 初始化为 1,将 b b b 初始化为 0
2.3. Implement with PyTorch
在 Pytorch 的 LayerNorm 类中有个 normalized_shape 参数,可以指定你要 Norm 的维度(注意,函数说明中 the last certain number of dimensions,指定的维度必须是从最后一维开始)。
比如我们的数据的 shape 是 [ 4 , 2 , 3 ] [4, 2, 3] [4,2,3],那么 normalized_shape 可以是 [ 3 ] [3] [3](最后一维上进行 Norm 处理),也可以是 [ 2 , 3 ] [2, 3] [2,3](Norm 最后两个维度),也可以是 [ 4 , 2 , 3 ] [4, 2, 3] [4,2,3](对整个维度进行 Norm),但不能是 [ 2 ] [2] [2] 或者 [ 4 , 2 ] [4, 2] [4,2],否则会报以下错误(以 normalized_shape = [2] 为例):
RuntimeError:
Given normalized_shape=[2],
expected input with shape [*, 2],
but got input of size[4, 2, 3]
提示我们传入的 normalized_shape = [2],接着系统根据我们传入的 normalized_shape 推理出期待的输入数据 shape 应该为 [ ∗ , 2 ] [*, 2] [∗,2]即最后的一个维度大小应该是 2 2 2,但我们实际传入的数据 shape 是 [ 4 , 2 , 3 ] [4, 2, 3] [4,2,3] 所以报错了
接着,我们再来看个示例,分别使用官方的 LN 方法和自己实现的 LN 方法进行比较:
import torch
import torch.nn as nn
def layer_norm_process(feature: torch.Tensor, beta=0., gamma=1., eps=1e-5):
var_mean = torch.var_mean(feature, dim=-1, unbiased=False)
# 均值
mean = var_mean[1]
# 方差
var = var_mean[0]
# layer norm process
feature = (feature - mean[..., None]) / torch.sqrt(var[..., None] + eps)
feature = feature * gamma + beta
return feature
def main():
t = torch.rand(4, 2, 3)
print(t)
# 仅在最后一个维度上做norm处理
norm = nn.LayerNorm(normalized_shape=t.shape[-1], eps=1e-5)
# 官方layer norm处理
t1 = norm(t)
# 自己实现的layer norm处理
t2 = layer_norm_process(t, eps=1e-5)
print("t1:\n", t1)
print("t2:\n", t2)
if __name__ == '__main__':
main()
经测试可以发现,结果是一样的
总结
参考资料1
参考资料2