关于线段树合并

线段树合并，顾名思义，就是将两个线段树合并成一个，并维护他们的各种信息。

---

二叉树合并

有下面两棵树：

![在这里插入图片描述](https://img-blog.csdnimg.cn/1bb70069eddd46c4a8563c54f671fa42.png#pic_center

如果我们把两棵树按相应的位置叠加在一起（不考虑信息处理），会变成这样：

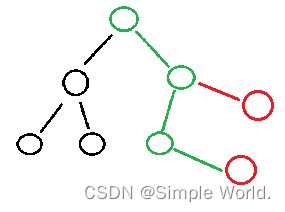
考虑一个合并以 $u$ 为根的子树和以 $v$ 为根的子树，有 $4$ 种情况：

1. $u$ 为空，$v$ 为空：不需要任何操作。
2. $u$ 不为空，$v$ 为空：$u$ 子树即为合并后的子树。
3. $u$ 为空，$v$ 不为空：$v$ 子树即为合并后的子树。
4. $u,v$ 都不为空：应该进一步合并 $u,v$ 的左子树，合并 $u,v$ 的右子树，可以把 $u$ 作为 $u,v$ 两个节点合并后的编号，左右孩子为分别合并后的相应结果。

如果我们把合并后的子树保存在 $u$ 为根的子树中，那么很容易编写函数 $merge(u,v)$：

int merge(int u,int v)//合并 u,v 子树，最后返回根节点合并后的节点编号
{
	if(!u||!v) return u+v;//前 3 中情况，如果都空则返回 0，如果 u 不空则返回 u，如果 v 不空则返回 v，只不过 u+v 刚好能同时满足 3 种情况，u^v 也可以
	lc[u]=merge(lc[u],lc[v]);
	rc[u]=merge(rc[u],rc[v]);
	return u; //如果两个都非空，则把 v 合并到 u 上
}

---

线段树合并

刚刚讲的二叉树合并其实就是为线段树服务。因为线段树本身就是二叉树，所以也就繁衍出线段树合并。

同时，线段树可能也会维护一些信息，在合并时要注意信息的合并。

1. 当 $u,v$ 至少一个为空，直接返回 $u+v$。
2. 当 $u,v$ 为叶子结点，边界合并 $v$ 到 $u$，维护 $u$ 的信息。
3. 当 $u,v$ 不是叶子结点，分别合并左子树和右子树，并用子节点更新父节点。

下面的代码演示的是在线段树合并（两个线段树子节点信息相加）时维护区间和的信息。

int merge(int u,int v,int l,int r)
{
	if(!u||!v)return u+v;
	if(l==r)
	{
		sum[u]+=sum[v]; //边界合并
		return u;
	}
	int mid=(l+r)/2;
	lc[u]=merge(lc[u],lc[v],l,mid);
	rc[u]=merge(rc[u],rc[v],mid+1,r);
	sum[u]=sum[lc[u]]+sum[rc[u]];  //儿子更新父亲
	return u;
}

---

时间复杂度

每一次线段树合并，其实只有在两棵树上有重复节点时才会递归，所以一次合并的时间就是两棵树重复的节点数。在更常见的情况下，多次合并时，每一次合并其实就已经去掉了重复的节点，算上线段树（动态开点）的耗时，设修改其中一棵线段树的次数为 $M$，线段树维护的数组总长度为 $N$，基本上复杂度都是 $O(MlogN)$。

---

题目类型1：并查集+线段树合并

P3224 永无乡

每一次建桥都用并查集合并两个岛，在每个岛上建立一棵线段树，维护并查集当前集合的每一个权出现次数。

#include
using namespace std;
const int maxn=500010;
int n,m,q,f[maxn],rt[maxn],tot,b[maxn],x,y,s[maxn],w[maxn];
char op;
struct node
{
	int lc,rc,sum;
}a[maxn*15];
void add(int &p,int l,int r,int x,int v)
{
	if(!p)p=++tot;
	if(l==r)
	{
		a[p].sum+=v;
		return;
	}
	int mid=l+r>>1;
	if(x<=mid)
	{
		add(a[p].lc,l,mid,x,v);
	}
	else
	{
		add(a[p].rc,mid+1,r,x,v);
	}
	a[p].sum=a[a[p].lc].sum+a[a[p].rc].sum;
}
int merge(int p,int q,int l,int r)
{
	if(!p||!q)return p+q;
	if(l==r)
	{
		a[p].sum+=a[q].sum;
		return p;
	}
	int mid=l+r>>1;
	a[p].lc=merge(a[p].lc,a[q].lc,l,mid);
	a[p].rc=merge(a[p].rc,a[q].rc,mid+1,r);
	a[p].sum=a[a[p].lc].sum+a[a[p].rc].sum;
	return p;
}
int find(int x)
{
	if(x==f[x])return x;
	return f[x]=find(f[x]);
}
void Merge(int x,int y)
{
	x=find(x);
	y=find(y);
	f[y]=x;
	s[x]+=s[y];
	merge(rt[x],rt[y],1,n);
}
int ask(int p,int l,int r,int k)
{
	if(l==r)
	{
		return l;
	}
	int mid=l+r>>1;
	if(a[a[p].lc].sum>=k)
	{
		return ask(a[p].lc,l,mid,k);
	}
	else
	{
		return ask(a[p].rc,mid+1,r,k-a[a[p].lc].sum);
	}
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&b[i]);
		w[b[i]]=i;
		f[i]=i;
		s[i]=1;
		add(rt[i],1,n,b[i],1);
	}
	for(int i=1;i<=m;i++)
	{
		scanf("%d%d",&x,&y);
		Merge(x,y);
	}
	scanf("%d",&q);
	while(q--)
	{
		scanf("\n%c%d%d",&op,&x,&y);
		if(op=='B')
		{
			Merge(x,y);
		}
		else
		{
			x=find(x);
			if(y>s[x])
			{
				printf("-1\n");
			}
			else printf("%d\n",w[ask(rt[x],1,n,y)]);
		}
	}
	return 0;
}

---

题目类型2：合并维护子树信息

在一棵树上，我们在 DFS 的过程中后序把每个节点的线段树合并，对于 $u$ 为根的子树，当 $u$ 的分支搜索并合并完后，就得到了整棵子树的信息。

P3521 ROT-Tree Rotations

当搜索完 $u$ 子树后，合并 $lc[u],rc[u]$，在分治合并的同时，计算子树 $rc[u]$ 中的数与 $lc[u]$ 中的数组成的逆序对。再维护一下子树大小，在交换和不交换中曲一个最小值。

#include
#define int long long
using namespace std;
const int maxn=400010;
int n,ch[maxn][2],a[maxn],tot,lc[maxn*10],rc[maxn*10],sum[maxn*10],cnt,rt[maxn],g,siz[maxn],ans;
int init(int p) //递归读入
{
	scanf("%lld",&a[++tot]);
	int s=tot;
	if(!a[s])
	{
		ch[s][0]=init(s);
		ch[s][1]=init(s);
	}
	return s;
}
void add(int &p,int l,int r,int x,int v)
{
	if(!p)p=++cnt;
	if(l==r)
	{
		sum[p]+=v;
		return;
	}
	int mid=l+r>>1;
	if(x<=mid)
	{
		add(lc[p],l,mid,x,v);
	}
	else
	{
		add(rc[p],mid+1,r,x,v);
	}
	sum[p]=sum[lc[p]]+sum[rc[p]];
}
int merge(int p,int q,int l,int r)
{
	if(!p||!q)return p^q;
	if(l==r)
	{
		sum[p]+=sum[q];
		return p;
	}
	int mid=l+r>>1;
	g+=sum[lc[p]]*sum[rc[q]];
	lc[p]=merge(lc[p],lc[q],l,mid);
	rc[p]=merge(rc[p],rc[q],mid+1,r);
	sum[p]=sum[lc[p]]+sum[rc[p]];
	return p;
}
void dfs(int u)
{
	if(ch[u][0])
	{
		dfs(ch[u][0]);
		dfs(ch[u][1]);
		siz[u]+=siz[ch[u][0]]+siz[ch[u][1]];
		g=0;
		merge(rt[ch[u][0]],rt[ch[u][1]],1,n);
		int tmp=siz[ch[u][0]]*siz[ch[u][1]];
		ans+=min(g,tmp-g);
		rt[u]=rt[ch[u][0]];
	}
	else
	{
		siz[u]=1;
		add(rt[u],1,n,a[u],1);
	}
}
signed main()
{
	scanf("%lld",&n);
	init(1);
	dfs(1);
	printf("%lld",ans);
	return 0;
}