平衡二叉树(AVL树)C/C++、C#代码实现
平衡二叉树是带有平衡条件的二叉查找树,指的是空树或者任一结点左、右高度差的绝对值不超过1的二叉树.
比如:
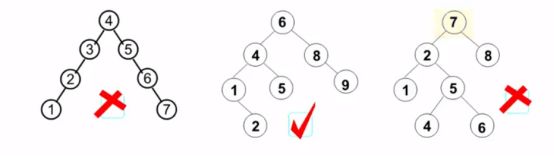
实现的难点在于,二叉树的平衡旋转
分为四种旋转,RR、LL、LR、RL旋转
RR旋转
LL旋转
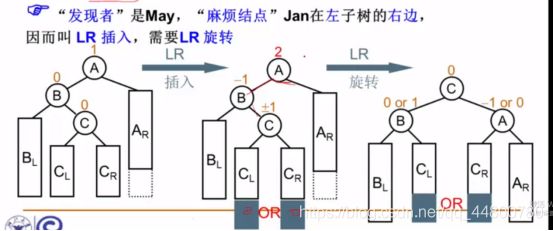
LR旋转
RL旋转
C/C++实现
#include s;
//while (temp || !s.empty())
//{
// while (temp) //一直向左将沿途结点压入栈
// {
// s.push(temp);
// temp = temp->left;
// }
// if (!s.empty())
// {
// temp = s.top();
// s.pop();
// std::cout << temp->element << " "; //先序遍历
// temp = temp->right;
// }
//}
//层序遍历,使用队列
//AVLNode * temp;
//queueq;
//if (t == nullptr)
// return;
//q.push(t);
//while (!q.empty())
//{
// temp = q.front();
// q.pop();
// std::cout << temp->element << " ";
// if (temp->left)
// q.push(temp->left);
// if (temp->right)
// q.push(temp->right);
//}
}
template<typename Comparable>
void AVLTree<Comparable>::rotateWithLeftChild(AVLNode *& k2)//左旋
{
AVLNode *k1 = k2->left;
k2->left = k1->right;
k1->right = k2;
k2->height = Max(height(k2->left), height(k2->right)) + 1;
k1->height = Max(height(k1->left), k2->height) + 1;
k2 = k1;//把所有的设置都变为改变后的设置
}
template<typename Comparable>
void AVLTree<Comparable>::rotateWithRightChild(AVLNode *& k2)//右旋
{
AVLNode *k1 = k2->right;
k2->right = k1->left;
k1->left = k2;
k2->height = Max(height(k2->right), height(k2->left)) + 1;
k1->height = Max(height(k1->right), k2->height) + 1;
k2 = k1;
}
template<typename Comparable>
void AVLTree<Comparable>::doubleWithLeftChild(AVLNode *& k3)//左右旋转
{
rotateWithRightChild(k3->left);
rotateWithLeftChild(k3);
}
template<typename Comparable>
void AVLTree<Comparable>::doubleWithRightChild(AVLNode *& k3)//右左旋转
{
rotateWithLeftChild(k3->right);
rotateWithRightChild(k3);
}
template<typename Comparable>
void AVLTree<Comparable>::balance(AVLNode *& t)
{
if (t == nullptr)
{
return;
}
if (height(t->left) - height(t->right) > ALLOWED_IMBLANCE)
if (height(t->left->left) >= height(t->left->right))
rotateWithLeftChild(t);
else
doubleWithLeftChild(t);
else if(height(t->right) - height(t->left) > ALLOWED_IMBLANCE)
if (height(t->right->right) >= height(t->right->left))
rotateWithRightChild(t);
else
doubleWithRightChild(t);
t->height = max(height(t->left), height(t->right)) + 1;
}
C#实现
public class AVLTree<T> where T : IComparable<T>
{
public class AVLNode
{
public T element;
public AVLNode Left;
public AVLNode Right;
public int Height;
public AVLNode(T e, AVLNode l, AVLNode r,int h = 0)
{
element = e;
Left = l;
Right = r;
Height = h;
}
};
private const int ALLOWED_IMBLANCE = 1;
private AVLNode Root;
public AVLTree()
{
Root = null;
}
public AVLTree(AVLTree<T> other)
{
Root = Clone(other.Root);
}
~AVLTree()
{
MakeEmpty();
}
private void Insert(T x,ref AVLNode t)
{
if(t == null)
{
t = new AVLNode(x, null, null);
}
else if (x.CompareTo(t.element) < 0)
{
Insert(x, ref t.Left);
if (Height(t.Left) - Height(t.Right) == 2)
if (x.CompareTo(t.Left.element) < 0)
RotateWithLeftChild(ref t);
else
DoubleWithLeftChild(ref t);
}
else if(x.CompareTo(t.element) > 0)
{
Insert(x, ref t.Right);
if (Height(t.Right) - Height(t.Left) == 2)
if (x.CompareTo(t.Right.element) > 0)
RotateWithRightChild(ref t);
else
DoubleWithRightChild(ref t);
}
t.Height = Max(Height(t.Left), Height(t.Right)) + 1;
}
private void Insert(ref AVLNode t,params T[] paramList)
{
foreach(var temp in paramList)
{
Insert(temp, ref t);
}
}
private void Remove(T x, ref AVLNode t)
{
if(t == null)
{
return;
}
if (x.CompareTo(t.element) < 0)
{
Remove(x, ref t.Left);
}
else if(x.CompareTo(t.element) > 0)
{
Remove(x, ref t.Right);
}
else if(t.Left != null && t.Right != null)
{
t.element = FindMin(t);
Remove(t.element, ref t.Right);
}
else
{
AVLNode oldNode = t;
t = t.Left ?? t.Right;
oldNode = null;
}
Balance(ref t);
}
private T FindMin(AVLNode t)
{
if (t != null)
while (t.Left != null)
t = t.Right;
return t.element;
}
private T FindMax(AVLNode t)
{
if (t != null)
while (t.Right != null)
t = t.Right;
return t.element;
}
private bool Contains(T x, AVLNode t)
{
while (t != null)
{
if (x.CompareTo(t.element) < 0)
t = t.Left;
else if (x.CompareTo(t.element) > 0)
t = t.Right;
else
return true;
}
return false;
}
private void MakeEmpty(ref AVLNode t)
{
if(t != null)
{
MakeEmpty(ref t.Left);
MakeEmpty(ref t.Right);
t = null;
}
}
private void PrintTree(AVLNode t)
{
if(t != null)
{
Console.WriteLine($"{t.element} ");
PrintTree(t.Left);
PrintTree(t.Right);
}
}
private AVLNode Clone(AVLNode t)
{
if(t == null)
{
return null;
}
return new AVLNode(t.element, Clone(t.Left), Clone(t.Right));
}
private int Max(int a, int b)
{
return (a > b) ? a : b;
}
private void RotateWithLeftChild(ref AVLNode k2)//左旋
{
AVLNode k1 = k2.Left;
k2.Left = k1.Right;
k1.Right = k2;
k2.Height = Max(Height(k2.Left), Height(k2.Right)) + 1;
k1.Height = Max(Height(k1.Left), k2.Height) + 1;
k2 = k1;
}
private void RotateWithRightChild(ref AVLNode k2)
{
AVLNode k1 = k2.Right;
k2.Right = k1.Left;
k1.Left = k2;
k2.Height = Max(Height(k2.Right), Height(k2.Left)) + 1;
k1.Height = Max(Height(k1.Right), k2.Height) + 1;
k2 = k1;
}
private void DoubleWithLeftChild(ref AVLNode k3)
{
RotateWithRightChild(ref k3.Left);
RotateWithLeftChild(ref k3);
}
private void DoubleWithRightChild(ref AVLNode k3)
{
RotateWithLeftChild(ref k3.Right);
RotateWithRightChild(ref k3);
}
private void Balance(ref AVLNode t)
{
if (t == null)
{
return;
}
if (Height(t.Left) - Height(t.Right) > ALLOWED_IMBLANCE)
if (Height(t.Left.Left) >= Height(t.Left.Right))
RotateWithLeftChild(ref t);
else
DoubleWithLeftChild(ref t);
else if (Height(t.Right) - Height(t.Left) > ALLOWED_IMBLANCE)
if (Height(t.Right.Right) >= Height(t.Right.Left))
RotateWithRightChild(ref t);
else
DoubleWithRightChild(ref t);
t.Height = Max(Height(t.Left), Height(t.Right)) + 1;
}
public bool Contains(T x)
{
return Contains(x, Root);
}
public bool IsEmpty()
{
return Root == null;
}
public void PrintTree()
{
PrintTree(Root);
}
public void MakeEmpty()
{
MakeEmpty(ref Root);
}
public void Insert(T x)
{
Insert(x, ref Root);
}
public void Insert(params T[] paramList)
{
Insert(ref Root, paramList);
}
public void Remove(T x)
{
Remove(x, ref Root);
}
public T FindMin()
{
return FindMin(Root);
}
public T FindMax()
{
return FindMax(Root);
}
public int Height(AVLNode t) { return t == null ? -1 : t.Height; }
}