【高级数据结构其一·并查集】
用于快速处理不相交集合的查询和合并问题
经典应用:连通子图,最小生成树Kruskal,最近公共祖先
#初始化
n=int(input())
s=[i for i in range(n+1)]
#查询
def find(x):
if x!=s[x]:
return find(s[x])
else:
return s[x]
#合并
def merge(x,y):
x=find(x)
y=find(y)
if x!=y:
s[x]=s[y]因为复杂度为O(n),效率太慢
路径压缩后,为O(1),效率大大提升
#路径压缩
def find(x):
if x!=s[x]:
s[x]=find(s[x])
return s[x]蓝桥幼儿园
n,m=map(int,input().split())
s=[i for i in range(n+1)]
def find(x):
if x!=s[x]:
s[x]=find(s[x])
return s[x]
def merge(x,y):
x=find(x)
y=find(y)
if x!=y:
s[x]=s[y]
for i in range(m):
op,x,y=map(int,input().split())
if op==1:
merge(x,y)
else:
if find(x)==find(y):
print('YES')
else:
print('NO')合根植物
n,m=map(int,input().split())
k=int(input())
s=list(range(m*n+1))
def find(x):
if x!=s[x]:
s[x]=find(s[x])
return s[x]
def merge(x,y):
x=find(x)
y=find(y)
if s!=y:
s[x]=s[y]
for i in range(k):
x,y=map(int,input().split())
merge(x,y)
cnt=0
for i in range(1,m*n+1):
if i==s[i]:
cnt+=1
print(cnt)修改数组
# 暴力法 ,40%,set判重O(1)
# n=int(input())
# a=[int(i) for i in input().split()]
# s=set()
# for i in range(n):
# while a[i] in s:
# a[i]+=1
# s.add(a[i])
# print(*a)
n=int(input())
a=[int(i) for i in input().split()]
s=list(range(int(1e6)))
def find(x):
if x!=s[x]:
s[x]=find(s[x])
return s[x]
for i in range(n):
root=find(a[i])#找到a[i]的根
a[i]=root#将a[i]的值改为a[i]
s[root]=find(root+1)#将a[i]的根加1
#也可以写成s[root]=root+1
print(*a)七段码
方法一:邻接表+枚举二进制状态+DFS连通新判断
mg=[[1,5],[0,2,6],[1,3,6],[2,4],[3,5,6],[0,4,6],[1,2,4,5]]
def dfs(x):
vis[x]=0
for i in mg[x]:
if vis[i]!=0:
dfs(i)
ans=0
for i in range(1,1<<7):
a=[]
s=bin(i)[2:]
s1='0' * (7 - len(s)) + s#补全7位二进制字符串
vis = [0] * 7#表示那些灯亮了
for i in range(len(s1)):
if s1[i]=='1':
vis[i]=1
cnt=0
for i in range(7):
if vis[i]!=0:
dfs(i)
cnt+=1
if cnt==1:
ans+=1
print(ans)#80方法二:邻接矩阵+DFS全排列枚举+并查集
mg=[[0]*7 for i in range(7)]
mg[0][1]=mg[0][5]=1
mg[1][0]=mg[1][2]=mg[1][6]=1
mg[2][1]=mg[2][3]=mg[2][6]=1
mg[3][2]=mg[3][4]=1
mg[4][3]=mg[4][5]=mg[4][6]=1
mg[5][0]=mg[5][4]=mg[5][6]=1
mg[6][1]=mg[6][2]=mg[6][4]=mg[6][5]=1
vis=[0]*7
s=[0]*7
def find(x):
if x!=s[x]:
s[x]=find(s[x])
return s[x]
def merge(x,y):
x=find(x)
y=find(y)
if x!=y:
s[x]=s[y]
def check():
for i in range(7):#注意,初始化一定要放函数里面,不然会每次操作会互相影响
s[i] = i
for i in range(7):
for j in range(7):
#注意,要同时满足亮和位置连通才是真正的连通
if mg[i][j] == 1 and vis[i]==1 and vis[j]==1:
merge(i, j)
flag = 0
for i in range(7):
if vis[i]==1 and s[i]==i:
flag+=1
if flag==1:
return True
return False
def dfs(n):
global cnt
if n==7:
if check():
cnt+=1
return
vis[n]=1
dfs(n+1)#第n位灯亮
vis[n]=0
dfs(n+1)#第n位灯不亮
cnt=0
dfs(0)
print(cnt)方法三:DFS全排列枚举+DFS连通性判断
笔者在此就不再详细写此方法
小猪存钱罐
def find(x):
if x!=s[x]:
s[x]=find(s[x])
return s[x]
def merge(x,y):
x=find(x)
y=find(y)
if x!=y:
s[x]=s[y]
n=int(input())
s=list(range(n+1))
for i in range(1,n+1):
j=int(input())
merge(i,j)
cnt=0
for i in range(1,n+1):
if i==s[i]:
cnt+=1
print(cnt)推导部分和
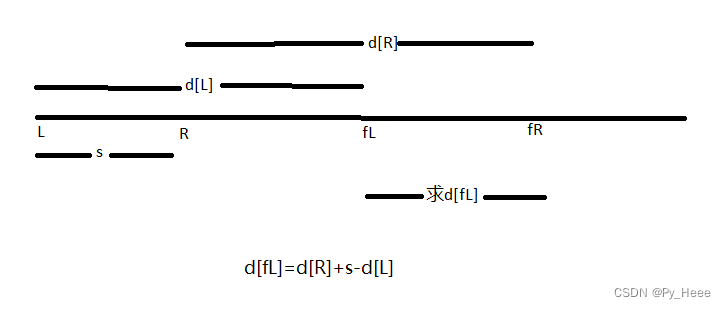
加权并查集
注意,1到5的距离实际为0到5的距离,即l到r,要看l-1到r
N,M,Q=map(int,input().split())
s=[0]*(N+1)
def init():
for i in range(N+1):
s[i]=i
def find(x):
if x!=s[x]:
t=s[x]
s[x]=find(s[x])
d[x]+=d[t]
return s[x]
init()
d=[0]*(N+1)
for i in range(M):
l,r,v=map(int,input().split())
fl=find(l-1)#
fr=find(r)
if fl!=fr:
s[fl]=s[fr]
d[fl]=d[r]+v-d[l-1]
ans=[]
for i in range(Q):
l,r=map(int,input().split())
if find(l-1)!=find(r):
ans.append('UNKNOWN')
else:
ans.append(d[l-1]-d[r])
for i in range(Q):
print(ans[i])直接输出会超时,笔者也不清楚怎么回事。
星球大战
正向思维,只能获得少部分分值
邻接矩阵版
n,m=map(int,input().split())
def find(x):
if x!=s[x]:
s[x]=find(s[x])
return s[x]
def merge(x,y):
x=find(x)
y=find(y)
if x!=y:
s[x]=s[y]
mg= [[0]*n for i in range(n)]
for i in range(m):
a,b=map(int,input().split())
mg[a][b]=1
mg[b][a]=1
k=int(input())
vis=[1]*n
s = list(range(n))
for i in range(k+1):
if i!=0:
vis[int(input())]=0
s = list(range(n))
for a in range(n):
for b in range(n):
if vis[b]==1 and vis[a]==1 and mg[a][b]==1:
merge(a,b)
cnt=0
for c in range(n):
if s[c]==c and vis[c]==1:
cnt+=1
print(cnt)邻接表版
n,m=map(int,input().split())
def find(x):
if x!=s[x]:
s[x]=find(s[x])
return s[x]
def merge(x,y):
x=find(x)
y=find(y)
if x!=y:
s[x]=s[y]
mg= [[] for i in range(n)]
for i in range(m):
a,b=map(int,input().split())
mg[a].append(b)
mg[b].append(a)
k=int(input())
vis=[1]*n
s = list(range(n))
for i in range(k+1):
if i!=0:
vis[int(input())]=0
s = list(range(n))
for a in range(n):
if vis[a] == 1:
for b in mg[a]:
if vis[b]==1:
merge(a,b)
cnt=0
for c in range(n):
if s[c]==c and vis[c]==1:
cnt+=1
print(cnt)反向思维
把破坏看成修复,即从初始有n-k个点时,先将这些点进行联系,计算一开始连通块的数量,然后开始逐渐增加点c,由邻接表得出点c与那些点连通,判断c是否与这些边
n,m=map(int,input().split())
def find(x):
if x!=s[x]:
s[x]=find(s[x])
return s[x]
def merge(x,y):
x=find(x)
y=find(y)
if x!=y:
s[x]=s[y]
mg= [[] for i in range(n)]
come=[0]*m
to=[0]*m
for i in range(m):
a,b=map(int,input().split())
mg[a].append(b)
mg[b].append(a)
come[i]=a
to[i]=b
broken=[1]*(n)
destroy=[]
k=int(input())
for i in range(k):
a=int(input())
broken[a]=0
destroy.append(a)
s=list(range(n))
res=n-k#一开始被破坏了k个点,还剩n-k个点,它们初始各为一个连通块
for i in range(m):#遍历所有的边
l=come[i];r=to[i]#取出每个边的两个端点
if broken[l]==1 and broken[r]==1 and find(l)!=find(r):# 如果两个端点都没被破坏
res-=1 #说明点l与r在一个连通块中,连通块数量-1
merge(l,r) #将其连接
ans=[res] #得到被破坏k个点后的连通块数量
for i in range(k-1,-1,-1):
c=destroy[i] #增添点c后,连通块情况
broken[c]=1 #修复点c
res+=1 #未确定c是否单独为一个连通块,先+1
for j in mg[c]:#遍历所有与c相连的点j
if broken[j]==1 and find(c)!=find(j):#如果j没被破坏
res-=1
merge(c,j)
ans.append(res)
for i in range(k,-1,-1):
print(ans[i])火星旅行
暴力法(枚举+模拟)+化换为链
n=int(input())
p=[0]*n
d=[0]*n
for i in range(n):
a,b=map(int,input().split())
p[i]=a
d[i]=b
p=p+p
d=d+d
for i in range(n):
p_sum=0
f1,f2=1,1
for j in range(i,i+n):
p_sum+=p[j]-d[j]
if p_sum<0:
f1=0
break
p_sum=0
for j in range(i+n,i,-1):
p_sum+=p[j]-d[j-1]#注意,距离变为j-1了。
if p_sum<0:
f2=0
break
if f1==1 or f2==1:
print('TAK')
else:
print('NIE')前缀和+单调队列
并查集
方格染色