K-means算法实现及分析
K-means算法对data中数据进行聚类分析
实验要求
-
- K-means算法对data中数据进行聚类分析
- 1. 算法原理描述
- 2. 写出K-means具体功能函数
- 3. 可视化画图,不同类数据采用不同颜色for item in range(k):
- 4. 完整代码
- 实验结果
- 感想
1. 算法原理描述
K-means算法是一种典型的无监督学习聚类算法。
而算法的具体思想是这样的:
- 从数据集中选择k个样本作为初始均值向量且分别带上其簇标记
(初始值的选择也是kmeans算法里的重要环节,但这里我首先尝试随机选择,可能在后续学习后会更新其他的方法) - 计算每一个样本与k个均值向量的距离,并带上与它距离最小的均值向量的簇标记,并放入对应集合里
(距离的计算也有很多方法,可能在后续学习后会更新其他的方法) - 计算集合的新的均值向量,若与上一次均值向量不一致,跳转至第二步骤开启新的一轮迭代;若与上一轮均值向量相同,则跳出循环,并将此时的均值向量和分类好的k个簇作为结果输出;
2. 写出K-means具体功能函数
- 载入数据:
def loadData(filename):
infile = open(filename, 'r')
x = []
y = []
for line in infile:
trainningset = line.split(' ', 1)
x.append(trainningset[0])
trainningset[1] = trainningset[1].replace('\n','')
y.append(trainningset[1])
x = [np.double(item) for item in x]
y = [np.double(item) for item in y]
return x, y
- 计算与簇中心的距离:
def distance(a,b,c,d):
return pow(pow((a-c),2)+pow((b-d),2), 0.5)
- 将每一个样本重新归类:
def iteration(k,meansx,meansy,x,y):
while 1:
Cx = [[] for i in range(k)]
Cy = [[] for i in range(k)]
ans = []
finalmeansx = []
finalmeansy = []
for item in range(len(x)):
mindis = 1000
minindex = -1
for ele in range(k):
if distance(x[item],y[item],meansx[ele],meansy[ele]) < mindis:
mindis = distance(x[item],y[item],meansx[ele],meansy[ele])
minindex = ele
ans.append(minindex)
Cx[minindex].append(x[item])
Cy[minindex].append(y[item])
for i in range(k):
finalmeansx.append(np.mean(Cx[i]))
finalmeansy.append(np.mean(Cy[i]))
if finalmeansx == meansx and finalmeansy == meansy:
break
else:
meansx = finalmeansx
meansy = finalmeansy
return finalmeansx,finalmeansy,Cx,Cy,ans
- kmeans主函数
def kmeans(k,x,y):
meansx = random.sample(x, k)
meansy = random.sample(y, k)
print(meansx)
print(meansy)
finalmeansx,finalmeansy,Cx,Cy,ans = iteration(k,meansx,meansy,x,y)
3. 可视化画图,不同类数据采用不同颜色for item in range(k):
f = open("E:\query.txt",'a')
for item in range(k):
f.write("第"+item.__str__()+"个簇:\n")
f.write("均值中心为("+finalmeansx[item].__str__()+","+finalmeansy[item].__str__()+")\n")
scatter(finalmeansx[item], finalmeansy[item],c=colors[item],marker='x')
f.write("簇内元素有:"+len(Cx[item]).__str__()+"个\n")
for i in range(len(Cx[item])):
f.write("("+Cx[item][i].__str__()+","+Cy[item][i].__str__()+")\n")
scatter(Cx[item][i],Cy[item][i],c=colors[item])
4. 完整代码
import matplotlib
import numpy as np
import random
from matplotlib.pyplot import plot, scatter
colors=['b','c','g','k','m','r','y']
#因为最后需要不同颜色绘图,但python不是很精通,所以最后采取了手动变色(滑稽
def loadData(filename): #把数据导入
infile = open(filename, 'r')
x = []
y = []
for line in infile:
trainningset = line.split(' ', 1)
x.append(trainningset[0])
trainningset[1] = trainningset[1].replace('\n','')
#这里也是因为我的python技术不精,不知道为啥划分后trainningset[1]后多了换行符,只好手动切除了
y.append(trainningset[1])
x = [np.double(item) for item in x]
y = [np.double(item) for item in y]
return x, y
def distance(a,b,c,d): #最简单的距离计算方法哈!
return pow(pow((a-c),2)+pow((b-d),2), 0.5)
def iteration(k,meansx,meansy,x,y):
#kmeans的核心函数,找到最终的均值向量
while 1:
Cx = [[] for i in range(k)]
Cy = [[] for i in range(k)]
ans = []
finalmeansx = []
finalmeansy = []
for item in range(len(x)):
mindis = 1000
minindex = -1
for ele in range(k):
if distance(x[item],y[item],meansx[ele],meansy[ele]) < mindis:
mindis = distance(x[item],y[item],meansx[ele],meansy[ele])
minindex = ele
ans.append(minindex)
Cx[minindex].append(x[item])
Cy[minindex].append(y[item])
for i in range(k):
finalmeansx.append(np.mean(Cx[i]))
finalmeansy.append(np.mean(Cy[i]))
if finalmeansx == meansx and finalmeansy == meansy:
break
else:
meansx = finalmeansx
meansy = finalmeansy
return finalmeansx,finalmeansy,Cx,Cy,ans
def kmeans(k,x,y):
meansx = random.sample(x, k)
meansy = random.sample(y, k)
print(meansx)
print(meansy)
finalmeansx,finalmeansy,Cx,Cy,ans = iteration(k,meansx,meansy,x,y)
#修改后代码:
f = open("E:\query.txt",'a')
for item in range(k):
f.write("第"+item.__str__()+"个簇:\n")
f.write("均值中心为("+finalmeansx[item].__str__()+","+finalmeansy[item].__str__()+")\n")
scatter(finalmeansx[item], finalmeansy[item],c=colors[item],marker='x')
f.write("簇内元素有:"+len(Cx[item]).__str__()+"个\n")
for i in range(len(Cx[item])):
f.write("("+Cx[item][i].__str__()+","+Cy[item][i].__str__()+")\n")
scatter(Cx[item][i],Cy[item][i],c=colors[item])
"""
#以下就是在输出框输出分类结果
for item in range(k):
print("第"+item.__str__()+"个簇:\n")
print("均值中心为("+finalmeansx[item].__str__()+","+finalmeansy[item].__str__()+")\n")
#最终簇中心用x突显
scatter(finalmeansx[item], finalmeansy[item],c=colors[item],marker='x')
print("簇内元素有:"+len(Cx[item]).__str__()+"个\n")
for i in range(len(Cx[item])):
print("("+Cx[item][i].__str__()+","+Cy[item][i].__str__()+")\n")
#画散点图
scatter(Cx[item][i],Cy[item][i],c=colors[item])"""
datax,datay = loadData("E:\data.txt")
k = int(input("请问需要分为几类:"))
kmeans(k,datax,datay)
#刚开始不知道为什么不弹出画图框,后来加了这个就出来啦
matplotlib.pyplot.figure(1)
matplotlib.pyplot.show()
实验结果
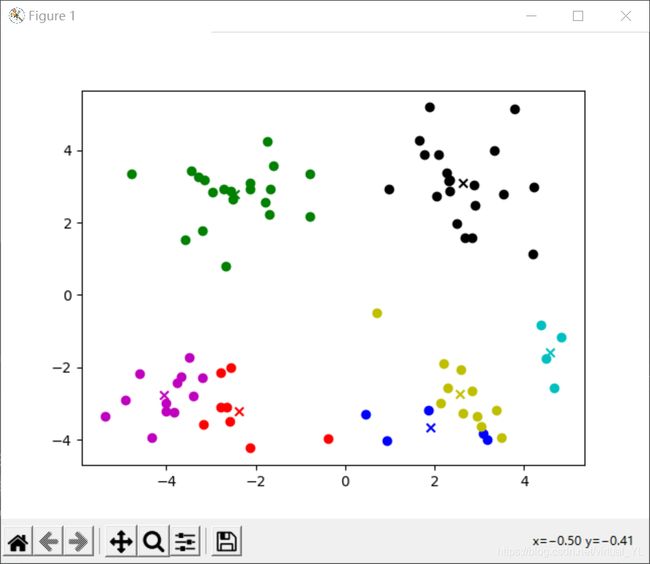
 (应该要把它导出到文件里的,再去修改修改!)
(应该要把它导出到文件里的,再去修改修改!)
改好了!
(又学到了!开心!)
将最后的数据生成txt文件存在了E盘里:
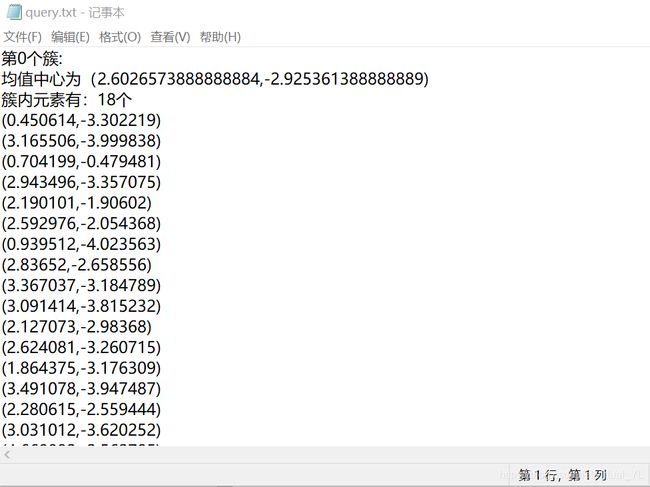
感想
- 其实之前只有在计算方法课上用过一段时间python,并没有自己主动地深入地学习过python,而对于数据处理和可视化,python有着其独特优势,希望在之后能够更多地学习了解python。
- 这次实验其实写的python代码很冗余,希望以后了解更多后能够加以修改!
- 先在E盘里找,找不到就自动创建
f = open("E:\query.txt",'a')
有问题的地方希望各位加以指正!