ARIMA序列分析
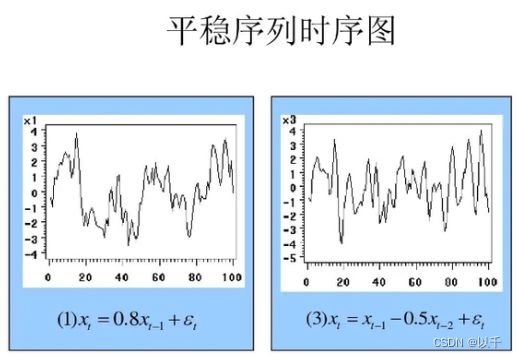
1. 什么是平稳序列
(stationary series):基本上不存在趋势的序列,各观察值基本上在某个固定的水平上波动或虽有波动,但并不存在某种规律,而其波动可以看成是随机的。
2. ARMA模型
ARIMA的优缺点
优点: 模型十分简单,只需要内生变量而不需要借助其他外生变量。(所谓内生变量指的应该是仅依赖于该数据本身,而不像回归需要其他变量)
缺点:
1.要求时序数据是稳定的(stationary),或者是通过差分化(differencing)后是稳定的。
2.本质上只能捕捉线性关系,而不能捕捉非线性关系。
ARIMA模型的几个特例
1.ARIMA(0,1,0) = random walk:
当d=1,p和q为0时,叫做random walk,每一个时刻的位置,只与上一时刻的位置有关。预测公式:Yt=μ+Yt−1
 2.1 主要应用场合
2.1 主要应用场合
平稳非白噪声的序列
2.2白噪声检查
lb=acorr_ljungbox(data.diff1.dropna(), lags = [i for i in range(1,12)],boxpierce=True)
LB检验P值均小于0.05,说明可以拒绝序列为白噪声的原假设,认为该数据不是随机数据,即该数据不是随机的,是有规律可循的,有分析价值。而序列X2的LB检验P值均大于0.05,说明该序列为白噪声,没有分析价值。
3. ACF、PACF
3.1 ACF
一个完整的自相关函数,可为我们提供具有滞后值的任何序列的自相关值。简单来说,它描述了该序列的当前值与其过去的所有值之间的相关程度。时间序列可以包含趋势,季节性,周期性和残差等成分。ACF在寻找相关性时会考虑所有这些成分。直观上来说,ACF 描述了一个观测值和另一个观测值之间的自相关,包括直接和间接的相关性信息。
3.2 PACF
是部分自相关函数或者偏自相关函数。基本上,它不是找到像ACF这样的滞后与当前的相关性,而是找到残差(在去除了之前的滞后已经解释的影响之后仍然存在)与下一个滞后值的相关性。因此,如果残差中有任何可以由下一个滞后建模的隐藏信息,我们可能会获得良好的相关性,并且在建模时我们会将下一个滞后作为特征。请记住,在建模时,我们不想保留太多相互关联的特征,因为这会产生多重共线性问题。因此,我们只需要保留相关功能。
直观上来说,PACF 只描述观测值yt和其滞后项yt-k之间的直接关系,调整了其他较短滞后项
(yt-1,yt-2,....... yt-k-1)的影响。
3.3 总的来说 ACF、PACF:
(1)ACF反映了当前时刻与前面所有时刻的线性相关程度,而PACF则反映了当前时刻与前面某些时刻的线性相关程度,并排除了其他时刻的影响。
(2)ACF的值可以表示为各个滞后阶数之间的关系,而PACF的值只表示当前时刻与前面某一时刻之间的关系。
(3)在AR模型中,PACF截尾于某个阶数k,意味着AR模型中只需要保留前k阶的滞后项;在MA模型中,ACF截尾于某个阶数k,则意味着MA模型中只需要保留前k阶的滞后误差。
4. Auto regressive (AR) process
转自:【时间序列】怎么理解ACF 和PACF_Alex Tech Bolg的博客-CSDN博客
当一个时间序列中,它当前的观测值可以通过历史观测值获得是,那么就是一个AR。
P 阶AR 过程可以写成下面的式子:
我们不能在这里使用ACF图,因为即使对于过去很久远的滞后项,它也会显示出良好的相关性。如果我们考虑了这么多特征,我们将遇到多重共线性问题。这对于PACF图来说不是问题,因为它删除了之前滞后已经解释的成分,因此我们只得到了与残差相关的滞后,比如未被较早的滞后项所解释的成分。
在下面的代码中,我定义了一个简单的AR 流程,并使用PACF 图找到了它的阶数。我们应该期望我们的AR过程在ACF图中显示出逐渐减少的趋势,因为作为一个AR过程,其当前与过去的滞后项具有良好的相关性。我们期望PACF在滞后项阶数后会急剧下降,因为这些接近当前项的滞后项可以很好地捕获变化,因此我们不需要很多过去的滞后项来预测当前项。
5. Moving average(MA) Process
转自:【时间序列】怎么理解ACF 和PACF_Alex Tech Bolg的博客-CSDN博客
Moving average(MA) Process 是一个序列,其中当前值是由过去误差的线性组合组成的。我们认为误差是服从正态分布并且相互独立的。q 阶MA 过程可以定义为下面的式子:
在这个例子中,飓风的影响只能保持一个滞后项。 这个例子中的飓风是一个独立现象。
MA 的阶数q 在里通过ACF 图获得,在阶数之后,ACF 会第一次穿过上限置信区间。根据上文我们知道,PACF 能够捕捉残差和时间序列滞后项的关系,我们可能能够从附近的滞后项和过去的滞后项得到很好的相关关系。为什么我们不用PACF呢?因为我们的序列是残差项的线性组合,并且时间序列本身的滞后项不能直接解释当前项(因为它并不是一个AR 过程)。PACF 图最核心的是,他能够提取已经被之前的滞后项所解释的变化,因此,在MA 过程中,PACF 失去了它的魔力。
另一方面,一个MA 过程,它并没有季节性或者趋势成分,因此ACF 能够捕捉只由于残差项带来的相关性。
在下面的代码中,我定义了一个简单的MA 流程,并使用ACF 图找到了它的阶数。我们应该期望ACF 图能够画出相邻的滞后项之间的良好的相关关系,并且在阶数q 之后迅速下降(因为这不是一个AR 过程,因此和过去的滞后项没有相关关系)。同样,我们也可以看到PACF 逐渐下降,临近的滞后项并不能预测当前项(不同于AR 过程);而更远的滞后项有可能有良好的相关关系。
6. 如何确定ARIMA模型p、q值?
6.1 理论依据
截尾:在大于某个常数k后快速趋于0为k阶截尾
拖尾:始终有非零取值,不会在k大于某个常数后就恒等于零(或在0附近随机波动)
确定差分阶数d。
如果时间序列数据不平稳,需要进行差分处理,使得数据平稳,差分阶数d可以通过观察时间序列的ACF和PACF图来确定。
确定自回归系数p和移动平均系数q。自回归系数p和移动平均系数q可以通过观察时间序列的ACF和PACF图来确定。如果ACF图在滞后阶数p之后截尾,而PACF图在滞后阶数q之后截尾,那么可以选择ARIMA(p,d,0)或者ARIMA(0,d,q)模型。如果ACF图和PACF图都在滞后阶数p和q之后截尾,那么可以选择ARIMA(p,d,q)模型。
确定季节性阶数P、Q和季节性差分阶数D。如果时间序列数据具有季节性,需要进行季节性差分处理,使得数据平稳,季节性差分阶数D可以通过观察时间序列的ACF和PACF图来确定。季节性阶数P和Q可以通过观察时间序列的季节性ACF和PACF图来确定。
6.2 方法1:观察法
数据data.xlsx
| time | value |
| 0.00 | 1.00 |
| 1.00 | 2.00 |
| 2.00 | 3.50 |
| 3.00 | 4.00 |
| 4.00 | 5.50 |
| 5.00 | 4.00 |
| 6.00 | 3.00 |
| 7.00 | 2.50 |
| 8.00 | 1.00 |
| 9.00 | 0.50 |
| 10.00 | -1.00 |
| 11.00 | -2.50 |
| 12.00 | -3.00 |
| 13.00 | -4.00 |
| 14.00 | -5.00 |
| 15.00 | -4.00 |
| 16.00 | -3.50 |
| 17.00 | -2.00 |
| 18.00 | -1.00 |
| 19.00 | 0.00 |
| 20.00 | 1.50 |
| 21.00 | 2.00 |
| 22.00 | 3.00 |
| 23.00 | 4.50 |
| 24.00 | 5.00 |
| 25.00 | 4.00 |
| 26.00 | 3.50 |
| 27.00 | 2.00 |
| 28.00 | 1.50 |
| 29.00 | 0.00 |
| 30.00 | -1.50 |
| 31.00 | -2.50 |
| 32.00 | -3.00 |
| 33.00 | -4.50 |
| 34.00 | -5.00 |
| 35.00 | -4.00 |
| 36.00 | -3.00 |
| 37.00 | -2.00 |
| 38.00 | -1.00 |
| 39.00 | 0.00 |
| 40.00 | 1.50 |
| 41.00 | 2.00 |
| 42.00 | 3.50 |
| 43.00 | 4.50 |
| 44.00 | 5.00 |
| 45.00 | 4.50 |
| 46.00 | 3.00 |
| 47.00 | 2.00 |
| 48.00 | 1.50 |
| 49.00 | 0.00 |
| 50.00 | -1.00 |
| 51.00 | -2.50 |
| 52.00 | -3.50 |
| 53.00 | -4.50 |
| 54.00 | -5.00 |
| 55.00 | -4.00 |
| 56.00 | -3.00 |
| 57.00 | -2.50 |
| 58.00 | -1.00 |
| 59.00 | 0.00 |
| 60.00 | 1.50 |
| 61.00 | 2.00 |
| 62.00 | 3.00 |
| 63.00 | 4.00 |
| 64.00 | 5.50 |
| 65.00 | 4.00 |
| 66.00 | 3.00 |
| 67.00 | 2.50 |
| 68.00 | 1.00 |
| 69.00 | 0.50 |
| 70.00 | -1.00 |
| 71.00 | -2.50 |
| 72.00 | -3.00 |
| 73.00 | -4.50 |
| 74.00 | -5.00 |
| 75.00 | -4.50 |
| 76.00 | -3.00 |
| 77.00 | -2.50 |
| 78.00 | -1.00 |
| 79.00 | 0.50 |
| 80.00 | 1.00 |
| 81.00 | 2.50 |
| 82.00 | 3.00 |
| 83.00 | 4.50 |
| 84.00 | 5.00 |
| 85.00 | 4.00 |
| 86.00 | 3.50 |
| 87.00 | 2.50 |
| 88.00 | 1.50 |
| 89.00 | 0.00 |
| 90.00 | -1.00 |
| 91.00 | -2.00 |
| 92.00 | -3.00 |
| 93.00 | -4.00 |
| 94.00 | -5.50 |
| 95.00 | -4.50 |
| 96.00 | -3.00 |
| 97.00 | -2.50 |
| 98.00 | -1.00 |
| 99.00 | 0.00 |
| 100.00 | 1.50 |
| 101.00 | 2.00 |
| 102.00 | 3.50 |
| 103.00 | 4.00 |
| 104.00 | 5.50 |
| 105.00 | 4.00 |
| 106.00 | 3.00 |
| 107.00 | 2.50 |
| 108.00 | 1.00 |
| 109.00 | 0.00 |
| 110.00 | -1.00 |
| 111.00 | -2.50 |
| 112.00 | -3.00 |
| 113.00 | -4.50 |
| 114.00 | -5.00 |
| 115.00 | -4.50 |
| 116.00 | -3.50 |
| 117.00 | -2.50 |
| 118.00 | -1.00 |
| 119.00 | 0.50 |
| 120.00 | 1.00 |
| 121.00 | 2.50 |
| 122.00 | 3.00 |
| 123.00 | 4.50 |
| 124.00 | 5.50 |
| 125.00 | 4.00 |
| 126.00 | 3.50 |
| 127.00 | 2.00 |
| 128.00 | 1.00 |
| 129.00 | 0.50 |
| 130.00 | -1.00 |
| 131.00 | -2.00 |
| 132.00 | -3.50 |
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
data = pd.read_excel('data.xlsx', index_col='time', parse_dates=True)
data.head()
# 计算一阶差分,这里因为data是稳定的,所以没用到一劫差分
diff = data.diff().dropna()
plot_acf(data)
plt.show()
plot_pacf(data)
plt.show()
根据这句话:
通过这个图,p在2以后截断了所以p,d,q(p=2, d=0,q=5)
6.3 计算法
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import pandas as pd
import numpy as np
import statsmodels.api as sm
data = pd.read_excel('data.xlsx', index_col='value', parse_dates=True)
data.head()
# 观察法===========================
diff = data.diff().dropna()
plot_acf(data)
plt.show()
plot_pacf(data)
plt.show()
# 计算法===========================
# 计算ACF和PACF
acf = sm.tsa.stattools.acf(data)
pacf = sm.tsa.stattools.pacf(data)
# 输出ACF和PACF的截尾点
q = np.argmax(acf < 0.05)
p = np.argmax(pacf < 0.05)
print(f'MA(q): {q}, AR(p): {p}')结果:
MA(q): 5, AR(p): 27. ARIMA数据拟合实践
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import pandas as pd
import numpy as np
import statsmodels.api as sm
from statsmodels.tsa.arima.model import ARIMA
data = pd.read_excel('data.xlsx', index_col='time', parse_dates=True)
data.head()
# 计算一阶差分
diff = data.diff().dropna()
plot_acf(data)
plt.show()
plot_pacf(data)
plt.show()
# 计算ACF和PACF
acf = sm.tsa.stattools.acf(data)
pacf = sm.tsa.stattools.pacf(data)
# 输出ACF和PACF的截尾点
q = np.argmax(acf < 0.05)
p = np.argmax(pacf < 0.05)
print(f'MA(q): {q}, AR(p): {p}')
#p,d,q
model = ARIMA(data, order=(p, 0, q))
model_fit = model.fit()
forecast = model_fit.forecast(steps=24)
# 输出预测结果
print(forecast)输出结果:
133 -4.433670
134 -4.499749
135 -4.044919
136 -3.366873
137 -2.414729
138 -1.222773
139 0.091940
140 1.400344
141 2.574036
142 3.497871
143 4.081265
144 4.267072
145 4.037184
146 3.414295
147 2.459660
148 1.267074
149 -0.046346
150 -1.351665
151 -2.520779
152 -3.438996
153 -4.016282
154 -4.196091
155 -3.960904
156 -3.333934
Name: predicted_mean, dtype: float64