【半监督医学图像分割 2023 CVPR】RCPS
文章目录
- 【半监督医学图像分割 2022 CVPR】RCPS
-
- 摘要
- 1. 介绍
- 2. 相关工作
-
- 2.1 医学图像分割
- 2.1 半监督学习
- 2.3 对比学习
- 3. 方法
-
- 3.1 整体概述
- 3.2 纠正伪监督
- 3.3 双向Voxel对比学习。
- 4. 实验
【半监督医学图像分割 2022 CVPR】RCPS
论文题目:RCPS: Rectified Contrastive Pseudo Supervision for Semi-Supervised Medical Image Segmentation
中文题目:RCPS:用于半监督医学图像分割的校正对比伪监督
论文链接:https://arxiv.org/abs/2301.05500
论文代码:https://github.com/hsiangyuzhao/RCPS
论文团队:上海交通大学&复旦大学上海医学院附属华山医院神经外科&上海科技大学
发表时间:2023年1月
引用:
引用数:
摘要
摘要医学图像分割方法通常被设计为全监督的,以保证模型的性能,这需要大量的专家注释样本,成本高,费力。 半监督图像分割可以利用大量未标记图像和有限的标记图像来缓解这一问题。
然而,由于伪标签中潜在的噪声和特征空间中的类可分性不足,从大量未标记图像中学习鲁棒的表示仍然是一个挑战,这削弱了现有半监督分割方法的性能。 针对上述问题,我们提出了一种新的半监督分割方法–校正对比伪监督(RCPS),该方法将校正伪监督和体素级对比学习相结合,以提高半监督分割的有效性。
特别地,我们设计了一种新的基于不确定度估计和一致性正则化的伪监督方法的校正策略,以减少伪标签中噪声的影响。 此外,在网络中引入双向体素对比损失,保证了特征空间中类内一致性和类间对比度,提高了分割中的类可分性。
本文提出的RCPS分割方法已经在两个公共数据集和一个内部临床数据集上进行了验证。 实验结果表明,与现有的半监督医学图像分割方法相比,该方法具有更好的分割性能。
1. 介绍
医学图像中解剖结构或病灶的准确、自动分割在临床实践中是非常迫切的,如图像引导介入、放射治疗、计算机辅助诊断等[1]。
随着深度学习技术的迅速发展,许多图像分割方法在医学图像定量分析方面显示出了其有效性。
然而,它们通常是以完全监督的方式设计的,这需要大量注释良好的数据来确保令人满意的性能。
虽然它适合于收集大量的医学图像作为训练数据集,但对这些样本进行相应的人工标注是相当昂贵和费力的,尤其是对CT、MRI等三维图像。 因此,开发自动分割方法以减少对大量标记训练样本的要求是非常重要的。
半监督分割是解决上述问题的一种很有前途的方法,它可以利用未标记的数据来提高分割性能,只需要少量的标记样本。 由于未标记样本的基本真理是不可用的,伪监督成为半监督学习的一种流行策略,它利用分割网络对未标记图像的预测作为伪标签来监督训练[2]。 基于伪监督的半监督学习可以分为两类。
第一类研究未标记数据的简单伪标记[3],以扩大训练数据集,并以离线方式训练学习算法。
第二类是基于一致性学习的在线培训。 它们通常从模型[4]、[5]或输入数据[6]-[8]中引入扰动,并鼓励扰动输入和伪标号的预测的相似性。
然而,尽管前人的研究取得了成功,但目前的伪监督方法还没有完全解决半监督医学图像分割中的两大挑战:
(1)半监督学习中伪标签的噪声特性:分割模型在预测过程中容易出错,从而降低伪监督的有效性;
(2)特征空间的监督不足:目前的半监督学习方法只提供标签空间的监督,而缺乏在特征空间的显式监督来进一步提高类的可分性。
针对上述问题,本文提出了一种改进的对比伪监督(RCPS)方法,用于医学图像的半光滑分割。 首先,我们提出了一种改进的伪监督策略来解决伪标签的噪声特性。 具体来说,我们生成了两个与原始输入不同外观的增强视图,并在模型预测中引入了基于不确定性估计和一致性正则化的伪标签校正。
这样,我们就可以使模型在图像外观的扰动下鲁棒地学习,减少伪监督中标签噪声的影响。 此外,我们引入了双向体素对比学习策略来解决特征空间中类可分性不足的问题。
由于传统的伪监督是在图像层监督,缺乏特征空间的监督,我们在特征层引入额外的监督,直接提高类的可分性。 这样可以减少特征空间中的类内方差,增加类间距离。
概括地说,这项工作的贡献由三个方面构成:
- 在图像空间中,我们引入了校正伪监督来学习不同外观下的鲁棒表示。 引入了预测不确定度估计和一致性正则化两种整改措施,提高了伪监管的有效性。
- 我们提出了一种双向体素对比丢失和一种新的自信负采样策略,以提高特征空间中不同语义类之间的可分性。 我们鼓励两个扩展视图应该相似,并且两个视图应该远离特征空间中的负样本。
- 我们在两个公共基准数据集上验证了所提出的RCPS,包括MRI中的左心房腔分割[9]和CT中的胰腺分割[10]。 实验结果表明,所提出的RCPS在两个基准上都优于其他现有的方法。 我们还包括一个内部临床数据集,用于创伤性脑损伤(TBI)患者的脑分割,与我们以前的工作相比,实现了最先进的分割性能。
2. 相关工作
2.1 医学图像分割
深度学习的发展极大地助推了语义分割的准确性[11]-[13]。 在医学图像分割中,U-Net[11]及其变体[12]、[14]、[15]因其高效、准确而得到了广泛的应用。 U-Net的主要优势在于其跳过连接的设计,其变体继续提高性能,其重点是通过网络拓扑修改[12]、[14]或通过注意力机制细化特征映射[15]、[16]来探索更好的特征表示。 近年来,Transformer[17]在医学图像分割方面也得到了广泛的关注。 陈等人。 [18]用变压器代替了U-NET中的编码器,增强了模型编码器的容量,从而提高了分割性能。 曹等。 [19]提出了一种类似U型网络的纯变压器网络SWIN-UNET,它用变压器块代替卷积块,以更好地提取特征。 尽管CNNS和Transformers在医学图像分割方面都取得了成功,但它们通常是以完全监督的方式设计的。 因此,这些全监督分割的性能改进受到标记训练样本的限制。
2.1 半监督学习
半监督学习算法基于三个核心假设[20]:(1)平滑性假设:相似的输入应该产生相似的输出,反之亦然; (2)低密度假设:同一类样本在特征空间中倾向于形成聚类,不同类的决策边界应该只经过特征空间中的低密度区域; (3)流形假设:位于同一低维流形上的样本应属于同一类。 大多数基于伪监督的半监督分割方法都遵循上述假设,并可分为两类,如第一节所述。第一类利用直接伪标记来扩大训练数据集。 李等人。 [3]提出用全监督算法的预测值作为未标记数据的伪标记。 然而,简单的伪标记会给训练过程引入大量的标签噪声。 为了解决这个问题,Sohn等人。 [7]提出对模型预测进行阈值化,只保留置信度高的预测,降低了误标率。 还有,郑等人。 [21]通过计算主输出和辅助输出之间的KL-散度来估计模型预测的不确定性,从而实现伪标签的自适应阈值化。 第二种方法利用伪标签在不同扰动下的一致性。 例如,Tarvainen等人。 [6]提出对同一输入生成两个不同的扩充视图,并使用教师模型的输出来监督学生模型。 瓦利等人。 [4]提出了一个多辅助解码器的分割模型,并鼓励主解码器和辅助解码器预测的一致性。 陈等人。 [5]提出了交叉伪监督,通过在两个不同参数初始化的模型的预测之间加强伪监督。
上述技术在医学图像分割中也比较流行。 均值教师框架的变体在医学图像分割中得到了广泛的应用[22]-[24]。 通过探索不同模型或任务的一致性,协同训练[25]和多任务学习[26]-[28]也相当流行。 此外,不确定性校正[29]-[31]也被广泛采用来提高模型的置信度。 与现有的只对基于不确定性的预测进行校正不同,本文引入一致性正则化和不确定性估计来进一步缓解伪监督的噪声性质,旨在提高图像外观扰动下分割的鲁棒性。
2.3 对比学习
对比学习是自监督学习中广泛采用的一种学习方法,它探索在没有任何注释的情况下学习有区别的特征表示[32]。 对比学习的核心思想是通过学习不同的特征表示来扩大特征空间中不同类别之间的距离,从而区分正对和负对。 为了实现显著特征提取,负样本的数量应该足够大,以使模型能够学习不同数据对的区分度。 现有的方法通常在训练过程中保持一个大的迷你批[33]、[34]或使用动量更新的记忆库[35]-[37]来保持大量的负样本。 对比学习在图像级任务中的成功启发研究者将其转移到密集预测任务中。 例如,Wang等人。 [38]将图像级对比学习改进到体素级,以提高分割性能。 像素对比学习也被广泛地用于半监督分割[28],[39],[40]。 钟等人。 [39]提出将像素对比学习和置信度抽样引入到半变量分割的一致性训练中,以提高分割能力。 赖等人。 [40]提出从同一输入生成两个不同的视图,并鼓励重叠区域的一致性和其他区域的双向对比。 本文在前人研究的基础上,对体素对比学习进行了改进和完善,在特征空间引入置信抽样和双向对比度计算,在特征层增加了直接监督,在图像层增加了校正伪监督,进一步提高了医学图像的半监督分割。
3. 方法
在本节中,我们介绍了 RCPS,这是一种半监督学习方法,它利用有限的标记数据和充足的未标记数据来提高医学图像的分割性能。我们首先概述了我们提出的 RCPS 方法,然后描述了 RCPS 中使用的学习策略,包括矫正伪监督和双向体素对比学习。
3.1 整体概述
在半监督分割中,我们假设训练数据集有一个包含 N 个标记数据的小标记子集和一个包含 M 个未标记数据的大未标记集,其中 m ≫ N m\gg N m≫N。为方便起见,我们将标记子集表示为 D l = { ( x i l , y i l ) } i = 1 N D_l=\{(x_i^l,y_i^l)\}_{i=1}^{N} Dl={(xil,yil)}i=1N未标注集为 D u = { ( x i u ) } i = 1 M \quad D_u=\{(x_i^u)\}_{i=1}^M Du={(xiu)}i=1M,其中 x i ∈ R H × W × D \begin{array}{r c l}{x_{i}}&{\in}&{\mathbb{R}^{H\times W\times D}}\\ \end{array} xi∈RH×W×D表示训练图像, y i ∈ B C × H × W × D y_i\in\mathbb{B}^{C\times H\times W \times D} yi∈BC×H×W×D表示训练标签(如果可用)。与仅使用标记子集 D l D_l Dl进行训练相比,半监督分割的训练目标是利用未标记子集 D u D_u Du中的图像来提高分割性能。
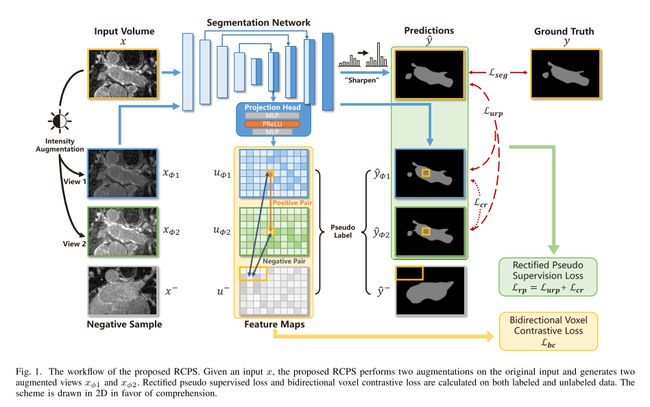
所提出的 RCPS 基于 U-Net 架构 [11],在第二个上采样块中有一个投影头用于计算对比损失,如图 1 所示。该框架在一次前向传递中包含四个数据输入:一个原始数据输入 x x x,从 x x x转换而来的两个增强视图 x ϕ 1 x_{\phi1} xϕ1和 x ϕ 2 x_{\phi2} xϕ2,以及一个用于双向体素对比学习的负输入 x − x^- x−。这些输入的 softmax 输出分别表示为 y ^ , y ^ ϕ 1 , y ^ ϕ 2 \hat{y},\hat{y}_{\phi1},\hat{y}_{\phi2} y^,y^ϕ1,y^ϕ2和 y − y^- y−。此外,对于双向体素对比学习, x ϕ 1 , x ϕ 2 x_{\phi1},x_{\phi2} xϕ1,xϕ2和 x − x^- x−的中间特征也由投影头输出,分别表示为 u ϕ 1 , u ϕ 2 u_{\phi1},u_{\phi2} uϕ1,uϕ2和 u−。
对于标注的数据,我们使用交叉熵损失和 Dice 损失的组合 [12] 来监督医学图像分割中流行的训练 :
L s e g ( y ^ , y ) = L c e ( y ^ , y ) + L D i c e ( y ^ , y ) , \mathcal{L}_{s e g}(\hat{y},y)=\mathcal{L}_{c e}(\hat{y},y)+\mathcal{L}_{D i c e}(\hat{y},y), Lseg(y^,y)=Lce(y^,y)+LDice(y^,y),
其中, Lce 表示交叉熵损失, LDice 表示 Dice 损失。
对于未标注的数据,我们计算得到修正的伪监督损失 L r p L_{rp} Lrp 和双向体素对比损失 L b c L_{bc} Lbc,这在 Sec中进行了讨论。 III-B 和 Sec。 分别为 III-C 。 总体无监督损失的计算方法如下 :
ℓ u n s u p = α L r p ( y ^ ϕ 1 , y ^ ϕ 2 , y ^ ) + β L b c ( u ϕ 1 , u ϕ 2 , u − ) \ell_{unsup}=\alpha\mathcal{L}_{rp}(\hat{y}_{\phi1},\hat{y}_{\phi2},\hat{y})+\beta\mathcal{L}_{bc}(u_{\phi1},u_{\phi2},u^{-}) ℓunsup=αLrp(y^ϕ1,y^ϕ2,y^)+βLbc(uϕ1,uϕ2,u−)
其中α和β是超参数,以平衡损失,具体任务取决于。
3.2 纠正伪监督
由于医学图像的外观各不相同,我们在半监督学习中采用了与先前工作[3] [7] [8] 一致的伪监督策略。具体来说,我们通过强度变换从原始输入生成两个增强视图,并在原始输入和原始输入的增强视图之间进行伪监督,以学习图像强度的扰动。然而,由于伪标签中的预测误差,伪监督可能会产生噪音,这会随后损害模型性能。我们建议通过预测不确定性估计和一致性正则化来纠正伪监督。插图已在图 1 中制作
-
伪监督:给定数据输入 x x x,我们执行两个不同的强度增强并获得两个不同的增强视图 x ϕ 1 x_{\phi1} xϕ1和 x ϕ 2 x_{\phi2} xϕ2。使用的增强涉及随机强度缩放、随机强度偏移和高斯噪声。通过在 Y Y Y和 y ^ ϕ i ( i = 1 , 2 ) \hat{y}_{\phi i}(i=1,2) y^ϕi(i=1,2)之间施加监督损失函数来执行伪监督。 通过这样做,我们鼓励模型学习健壮的表示,尽管数据外观不同。 在实践中,我们通过用温度超参数 T 来划分 Logits (软 max 激活前的模型输出 ) 来增强软最大值概率 y ,以确保半监督学习中的低密度假设,这在 Sec中已经讨论过。 II-B . 这种操作可以使伪标签 "更难 " ,避免类重叠。 因此,伪监管损失定义如下 :
L p ( y ^ ϕ i , y ^ ) = L c e ( y ^ ϕ i , σ ( z / T ) ) , \mathcal L_p(\hat y_{\phi i},\hat y)=\mathcal L_{ce}(\hat y_{\phi i},\sigma(z/T)), Lp(y^ϕi,y^)=Lce(y^ϕi,σ(z/T)),
其中 z 表示 x的逻辑, σ 表示软 max 函数, T 是温度。 -
不确定性估计:模型预测之间的直接伪监督有时可能是不可靠的,因为模型预测中可能出现错误,这导致了伪监督的噪音性质。 对假监督的预测不确定性估计和一致性规范化进行了介绍,以减轻标签噪声在伪监督中的影响。伪监督容易受到标签噪声的影响,因此对伪标签进行高置信度阈值处理是降低标签噪声的常用方法[7]。然而,简单地用硬阈值对概率进行阈值化并不适合分割任务,因为不同语义类的分割难度是可变的。硬阈值化可以使困难类更难通过阈值,从而导致偏离背景类的有偏预测。
我们建议使用模型预测的不确定性来纠正伪监管,这是由KL发散 [21] 计算的。 有了不确定性估计,不确定性校正伪监控损失的定义如下 :
L u r p ( y ^ ϕ i , y ^ ) = e − D k l ( y ^ ϕ i , y ^ ) L p ( y ^ ϕ i , y ^ ) + D k l ( y ^ ϕ i , y ^ ) , D k l ( y ^ ϕ i , y ^ ) = y ^ log ( y ^ y ^ ϕ i ) . \begin{array}{c}\mathcal{L}_{urp}(\hat{y}_{\phi i},\hat{y})=e^{-\mathcal{D}_{kl}(\hat{y}_{\phi i},\hat{y})}\mathcal{L}_p(\hat{y}_{\phi i},\hat{y})+\mathcal{D}_{kl}(\hat{y}_{\phi i},\hat{y}),\\ \mathcal{D}_{kl}(\hat{y}_{\phi i},\hat{y})=\hat{y}\log(\frac{\hat{y}}{\hat{y}_{\phi i}}).\end{array} Lurp(y^ϕi,y^)=e−Dkl(y^ϕi,y^)Lp(y^ϕi,y^)+Dkl(y^ϕi,y^),Dkl(y^ϕi,y^)=y^log(y^ϕiy^).
不确定性估计引入了对伪监控损失的自适应体素加权,其中自信的体素具有较高的权重,而不太自信的体素具有较低的权重。 这种整流降低了标签噪声的影响,提高了分割的鲁棒性。 -
一致性规则化:基于半监督学习中的平稳性假设,我们预计xφ1和xφ2的预测应该是相似的,尽管强度转换产生的外观不同。 因此,我们引入一致性规则化,进一步纠正伪监督,以尽量减少 ˆyφ1与 ˆyφ2之间的分歧。 我们采用了从两种不同观点预测之间的余弦距离:
L c r ( y ^ ϕ 1 , y ^ ϕ 2 ) = 1 − cos ( y ^ ϕ 1 , y ^ ϕ 2 ) , cos ( y ^ ϕ 1 , y ^ ϕ 2 ) = y ^ ϕ 1 ⋅ y ^ ϕ 2 ∥ y ^ ϕ 1 ∥ 2 ⋅ ∥ y ^ ϕ 2 ∥ 2 . \begin{array}{c}\mathcal{L}_{cr}(\hat{y}_{\phi1},\hat{y}_{\phi2})=1-\cos(\hat{y}_{\phi1},\hat{y}_{\phi2}),\\ \cos(\hat{y}_{\phi1},\hat{y}_{\phi2})=\dfrac{\hat{y}_{\phi1}\cdot\hat{y}_{\phi2}}{\|\hat{y}_{\phi1}\|_2\cdot\|\hat{y}_{\phi2}\|_2}.\end{array} Lcr(y^ϕ1,y^ϕ2)=1−cos(y^ϕ1,y^ϕ2),cos(y^ϕ1,y^ϕ2)=∥y^ϕ1∥2⋅∥y^ϕ2∥2y^ϕ1⋅y^ϕ2.
尽量减少伪监督损失可以隐含地减少预测之间的距离,但明确的损失术语有助于在训练过程中更正规化,这有助于稳定训练过程。最后的伪监督损失是不确定性整改伪监督损失和一致性规范化的线性组合。
L r p ( y ^ ϕ 1 , y ^ ϕ 2 , y ^ ) = L u r p ( y ^ ϕ 1 , y ^ ) + L u r p ( y ^ ϕ 2 , y ^ ) + L c r ( y ^ ϕ 1 , y ^ ϕ 2 ) . \begin{array}{c}\mathcal{L}_{rp}(\hat{y}_{\phi1},\hat{y}_{\phi2},\hat{y})=\mathcal{L}_{urp}(\hat{y}_{\phi1},\hat{y})+\mathcal{L}_{urp}(\hat{y}_{\phi2},\hat{y})\\ +\mathcal{L}_{cr}(\hat{y}_{\phi1},\hat{y}_{\phi2}).\end{array} Lrp(y^ϕ1,y^ϕ2,y^)=Lurp(y^ϕ1,y^)+Lurp(y^ϕ2,y^)+Lcr(y^ϕ1,y^ϕ2).
在实践中,我们从计算图中分离 ˆyv,以阻止这个分支中的梯度,以便梯度只能回传到增强视图的分支。
3.3 双向Voxel对比学习。
基于半监督学习的平稳假设,我们预计除了标签空间一致性之外,特征空间一致性。 这可以通过在功能映射之间使用 ℓ 1 \ell_{1} ℓ1或 ℓ 2 \ell_{2} ℓ2的损失来实现。 然而,这种损失太弱,无法在训练期间提供足够的监督,并且无法将正样推向负样本。 相反,我们建议利用对比学习,鼓励半监督学习中不同的特征表征表征。 受现有作品的启发,我们开发了一个双向的体素对比损失来完成这一点,这见图1。 来自 u ϕ 1 u_{\phi1} uϕ1和 u ϕ 1 u_{\phi1} uϕ1的空间对应位置的Voxel对被视为正数,而与它们共享不同语义类的体素则被视为负数。 积极因素被拉在一起,以减少类内的距离,并从负值中推开,以确保不同类之间的较大边距。 正式地给定锚 ψ 1 ∈ u ϕ 1 \psi_1\in u_{\phi1} ψ1∈uϕ1,体对比损失计算如下:
L c ( ψ 1 , ψ 2 ) = − log e cos ( ψ 1 , ψ 2 ) / τ e cos ( ψ 1 , ψ 2 ) / τ + ∑ ψ n ∈ ω − n = 1 N e cos ( ψ 1 , ψ n ) ) / τ , {\mathcal{L}}_{c}(\psi_{1},\psi_{2})=-\log\frac{e^{\cos(\psi_{1},\psi_{2})/\tau}}{e^{\cos(\psi_{1},\psi_{2})/\tau}+\sum_{\psi_{n}\in\omega-n=1}^{N}e^{\cos(\psi_{1},\psi_{n}))/\tau}}, Lc(ψ1,ψ2)=−logecos(ψ1,ψ2)/τ+∑ψn∈ω−n=1Necos(ψ1,ψn))/τecos(ψ1,ψ2)/τ,
其中, ψ 2 \psi_2 ψ2表示从xφ2中提取的特征图uφ2中的正体素,φn表示负体素,u-表示包含负样本的特征图,n是采样的负体素的个数,τ是温度超参数。
然而,尽管对比学习在像素级自我监督任务中取得了成功,但很难将现有的像素级特征表示方法转移到语义分割中。 在图像分割中,同一幅图像中的不同体素可以属于不同的类,尤其是对于通常覆盖面积较大的背景类。 因此,随机抽样可以对与锚定体素共享同一类的大量体素进行抽样。 高的假阴性率会导致模型训练混乱,导致决策边界模糊,从而损害分割性能。
为了避免这些问题,我们利用在前向传递过程中计算的伪标记来对负体素进行采样。 我们提出了一种新的自信负采样策略来对负体素进行采样。 给定锚定体素 ψ i ( i = 1 , 2 ) , \psi_{i}(i=1,2), ψi(i=1,2),,从u-中提取负样本,从x-中计算出u-。 计算伪标号y-并排除同类别的样本,且该样本具有 ψ i ( i = 1 , 2 ) \psi_{i}(i=1,2) ψi(i=1,2)。 然后,根据预测置信度对负体素进行采样,选取前k个最具置信度的样本。 与随机采样相比,该策略降低了采样过程中的假阴性率,从而提高了系统的性能。
注意,两个增强视图都应该从负样本中移开。 因此,我们通过交换φ1和φ2的位置来计算另一个对比损失。 因此,双向体素对比损失定义如下:
L b c ( ψ 1 , ψ 2 ) = L c ( ψ 1 , ψ 2 ) + L c ( ψ 2 , ψ 1 ) . \mathcal{L}_{bc}(\psi_1,\psi_2)=\mathcal{L}_c(\psi_1,\psi_2)+\mathcal{L}_c(\psi_2,\psi_1). Lbc(ψ1,ψ2)=Lc(ψ1,ψ2)+Lc(ψ2,ψ1).
在实际应用中,我们计算了 u ϕ 1 u_{\phi1} uϕ1和 u ϕ 2 u_{\phi2} uϕ2中每个位置的双向体素对比损失。 因此,总损失计算如下:
L b c ( u ϕ 1 , u ϕ 2 , u − ) = 1 N u ∑ ψ 1 ∈ u ϕ 1 L b c ( ψ 1 , ψ 2 ) , \mathcal{L}_{bc}(u_{\phi1},u_{\phi2},u^{-})=\frac{1}{N_{u}}\sum_{\psi_{1}\in u_{\phi1}}\mathcal{L}_{bc}(\psi_{1},\psi_{2}), Lbc(uϕ1,uϕ2,u−)=Nu1ψ1∈uϕ1∑Lbc(ψ1,ψ2),
其中 N u N_{u} Nu表示 u ϕ i ( i = 1 , 2 ) . u_{\phi i}(i=1,2). uϕi(i=1,2).中的体素个数。