数据结构与算法学习 02 树与二叉树
树与二叉树
树
- 树形结构是一种非线性数据结构。
- 树中的每个部分称为节点(或结点),节点间存在分支结构和层次关系。
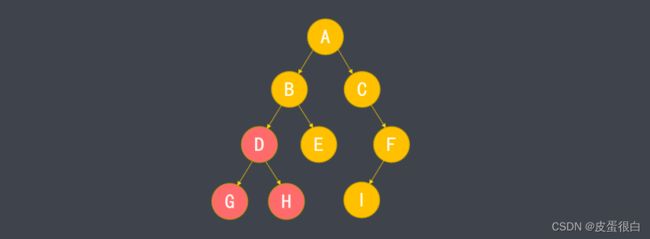
- 每个树形结构都具有一个根节点(A)。
- 根据节点之间的关系,也存在父节点(A 是 B 的父节点)、子节点(B 是 A 的子节点)、兄弟节点(B 和 C)的概念。
- 不含子节点的节点称为叶节点(G、H、I)。
- 子树:对某个节点与其后代节点的整体称呼。
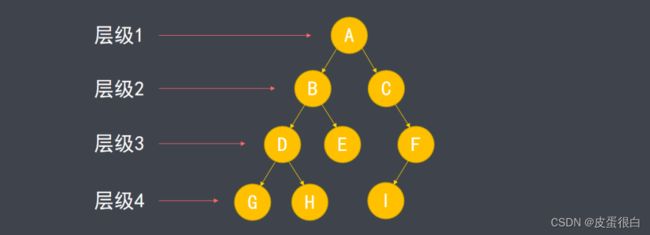
- 由于存在父子关系,树种的节点形成多级结构,称为层级。
- 根节点层级为 1,向下依次递增。
- 树中最深节点的层级称为树的高度(4)。
二叉树
除了常规的树形结构,为了提高运算和搜索效率,还有一个非常常用的树形结构:二叉树。
- 二叉树是树形结构中的一种,二叉树的每个节点最多只能存在 2 个子节点。
- 二叉树中的节点又称为左子节点(B)和右子节点(C、F)。
- 从左右两个节点分出的子树,又可称为左子树(B、D、E、G、H)和右子树(C、F、I)。
注意:这里的 F 是右子节点,用数组表示 C 的子节点时,可以用
null为左子节点占位,如 上图树结构可以用数组表示为[A, B, C, D, E, null, F, G, H, null, null, I]
- 除普通二叉树外,还存在一些特殊形式的二叉树。
- 如上图,二叉树的每层节点都达到最大值,称为满二叉树。
- 二叉树除最后一层外,每层节点都达到最大值,且最后一层节点都位于左侧,这种形式称为完全二叉树。
- 满二叉树也属于完全二叉树。
二叉树的存储形式
对于不同的二叉树形式可以使用不同的存储方式。
- 完全二叉树的结构连续,有迹可循,可采用顺序存储方式。
- 按照从左往右,再从上到下的顺序将节点存储在数组中。
- 普通二叉树由于结构不规则,不适合使用顺序存储,为了记录节点间的关系,可使用链式存储方式。
- 每个节点通过
value表示值,left、right表示左右子节点。
- 每个节点通过
二叉树的遍历方式
-
深度优先搜索算法(DFS:Depth First Search)
- 二叉树的遍历从根节点开始,以找到最深层叶节点为目的,快速找到最深的位置然后再向回进行处理
- 根据节点操作的顺序不同存在三种遍历形式:前序遍历、中序遍历、后序遍历。
- 序表示树根节点的访问顺序。
-
广度优先搜索算法(BFS:Breadth First Search)
- 也称为层序遍历,即逐层地,从左到右访问所有节点。
前序遍历
根节点最先进行操作,按 根节点 -> 左子树 -> 右子树 顺序进行遍历。
- 首先处理根节点 A,然后处理 A 的左子树,对于子树的遍历也要遵循前序遍历规则,于是处理 A 的左子树的根节点 B,D 是 B 的左子树的根节点,所以处理完 B 就会处理 D。
- 如图的前序遍历结果为:
A -> B -> D -> G -> H -> E -> C -> F -> I
中序遍历
根节点在中间进行操作,按 左子树 -> 根节点 -> 右子树 顺序进行遍历。
- 首先找到 A 的左子树,然后是 B 的左子树,一直找到 G 进行处理,然后处理 G 的根节点 D,接着是 D 的右子树。
- 如图的中序遍历结果为:
G -> D -> H -> B -> E -> A -> C -> I -> F,请注意 F 是 C 的右子节点,所以此处 C 优先于 F 操作。
后序遍历
根节点在最后进行操作,按 左子树 -> 右子树 -> 根节点 顺序进行遍历。
- 如图的后序遍历结果为:
G -> H -> D -> E -> B -> I -> F -> C -> A
层序遍历
逐层地,从左到右访问所有节点。
- 如图的层序遍历结果为:
A -> B -> C -> D -> E -> F -> G -> H
LeetCode 精选题目
二叉树的前序遍历
链接:144. 二叉树的前序遍历
给你二叉树的根节点 root,返回它节点值的前序遍历。
示例:
// 示例1:
1
\
2
/
3
// 注意 2 是右子节点
输入: root = [1, null, 2, 3]
输出: [1, 2, 3]
// 示例2
输入: root = []
输出: []
// 示例3
输入: root = [1]
输出: [1]
// 示例4
1
/
2
// 注意 2 是左子节点
输入: root = [1, 2]
输出: [1, 2]
// 示例5
1
\
2
// 注意 2 是右子节点
输入: root = [1, null, 2]
输出: [1, 2]
进阶:递归算法很简单,你可以通过迭代算法完成吗?
递归算法
/**
* 树节点的结构
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var preorderTraversal = function (root) {
// 用于存储遍历的结果
const res = []
// 设置函数用于进行递归遍历
const preorder = root => {
// 当前节点为空时,无序进行递归操作
if (root === null) {
return
}
// 记录根节点值
res.push(root.val)
// 前序遍历左子树
preorder(root.left)
// 前序遍历右子树
preorder(root.right)
}
preorder(root)
return res
}
使用递归算法非常适合遍历树形结构,采用前序、中序、后序遍历的区别,就在于下面这段代码的执行顺序:
// 记录根节点值
res.push(root.val)
// 前序遍历左子树
preorder(root.left)
// 前序遍历右子树
preorder(root.right)
迭代算法
解题思路:
维护一个栈结构,由于前序遍历在操作完根节点后优先操作左子树,遍历节点的时候将右子节点(不论是否是 null)入栈,栈中存储的就是等待操作的节点,当遍历完左子树,再从栈中提取右子节点依次操作,操作右子树也遵循前序遍历的顺序进行入栈出栈。
var preorderTraversal = function (root) {
const res = []
const stack = []
while (root !== null || stack.length) {
while (root !== null) {
// 右子节点入栈
stack.push(root.right)
// 记录根节点
res.push(root.val)
// 下一步处理左子节点
root = root.left
}
// 左子树处理完毕,将 stack 出栈,处理右子树
root = stack.pop()
}
return res
}
二叉树的最大深度
链接:104. 二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
示例:
3
/ \
9 20
/ \
15 7
给定的二叉树 [3,9,20,null,null,15,7]
返回它的最大深度 3
解题思路:
之前递归前序遍历二叉树操作时使用的方式称为深度优先搜索算法,以找到最深层叶节点为目的,计算二叉树最大深度同样可以采用这种方式。
/**
* @param {TreeNode} root
* @return {number}
*/
var maxDepth = function (root) {
if (!root) {
return 0
}
return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1
}
二叉树的层序遍历
链接:102. 二叉树的层序遍历
给你二叉树的根节点root,返回其节点值的层序遍历。(即逐层地,从左到右访问所有节点)。
注意:返回的是一个二维数组结构,每个元素是每层的节点组成的数组。
示例:
// 示例1
3
/ \
9 20
/ \
15 7
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
// 示例2
输入:root = [1]
输出:[[1]]
// 示例3
输入:root = []
输出:[]
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[][]}
*/
var levelOrder = function (root) {
if (root === null) {
return []
}
const res = []
// 声明队列用于存储后续数据
const queue = [root]
// 遍历队列
while (queue.length) {
// 针对本轮操作,创建一个新的数组
const arr = []
// 记录本轮要遍历的节点数量
let len = queue.length
while (len-- > 0) {
// 将本次操作的节点出队
const node = queue.shift()
// 记录节点值
arr.push(node.val)
// 检测是否存在左右子节点,如果右,入队即可
node.left && queue.push(node.left)
node.right && queue.push(node.right)
}
// 记录本轮遍历的节点
res.push(arr)
}
return res
}
二叉搜索树
- 二叉搜索树是一种特殊的二叉树,简称 BST(Binary Search Tree)
- 二叉搜索树的特点是左子树的节点都小于根节点,右子树的节点都大于根节点
- 这个规则也适用于子树,即子树也为二叉搜索树
LeetCode 精选题目
验证二叉搜索树
链接:98. 验证二叉搜索树
给你一个二叉树的根节点 root,判断其是否是一个有效的二叉搜索树。
有效二叉搜索树的定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例:
// 示例1
2
/ \
1 3
输入:root = [2,1,3]
输出:true
// 示例2
5
/ \
1 4
/ \
3 6
输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。
解题思路:
创建一个辅助函数,递归检测节点是否符合条件,向函数传入比较的上限和下限;对于左子节点,上限就是当前节点,下限就是当前节点检测的下限(即当前节点作为右子节点的父节点或无限);对于右子节点,上限就是当前节点检测的上限(即当前节点作为左子节点的父节点或无限),下限就是当前节点;根节点的上限为 Infinity,下限为 -Infinity。
/**
* @param {TreeNode} root
* @return {boolean}
*/
var isValidBST = function (root) {
return helper(root, -Infinity, Infinity)
}
/**
*
* @param {*} root 检测的节点
* @param {*} lower 下限
* @param {*} upper 上限
*/
function helper(root, lower, upper) {
if (root === null) {
return true
}
// 检测当前节点值是否超出边界
if (root.val >= upper || root.val <= lower) {
return false
}
// 当前节点通过检测,再检测左右子节点
return helper(root.left, lower, root.val) && helper(root.right, root.val, upper)
}
利用二叉树的中序遍历验证二叉搜索树
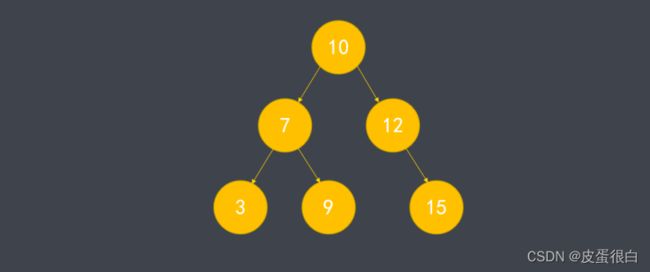
图例的中序遍历结果:[3, 7, 9, 10, 12, 15]
可以发现中序遍历二叉搜索树的结果是一个升序列表,所以要验证一个二叉搜索树,就可以对其进行中序遍历,下一个节点总是大于上一个节点,则验证成功,否则验证失败。
之前的解题思路是一个递归遍历方式,下面使用中序遍历的迭代方式进行解题:
var isValidBST = function (root) {
const stack = []
// 声明一个变量,记录当前操作的节点,用于与下次获取的节点进行比较
let oldNode = -Infinity
while (root !== null || stack.length) {
while (root !== null) {
stack.push(root)
root = root.left
}
root = stack.pop()
if (root.val <= oldNode) {
return false
}
oldNode = root.val
root = root.right
}
return true
}