0301概述-最小生成树-图-数据结构和算法(Java)
1 最小生成树
加权图:加权图是一种为每条边关联一个权值或者成本的图模型。
比如在一幅航空图中,边表示航线,权值则可以表示距离或者费用。
最小生成树。 图的生成树是它的一棵含有所有顶点的无环连通子图。一幅加权图的最小生成树(MST)是它的一棵权值(树中所有边的权值之和)最小的生成树。
-
一些约定
- 只考虑连通图。
- 边的权值不一定表示距离。 权值也可以表示时间、费用或者其他完全不同的量。
- 边的权值可能是0或者负数。
- 所有边的权值都各不相同。 如果不同边的权重相同,最小生成树就不一定唯一。存在多棵最小生成树使部分算法证明变得更加复杂,因此我们在表示时排除这种可能。
总之,我们在学习最小生成树相关算法过程中假设任务是在一幅加权连通无向图中找到它的最小生成树。
2 原理
树的两个重要的性质,如下图2-1所示:
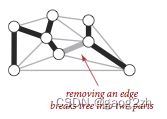
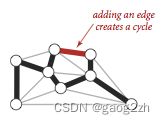
- 用一条边连接树中任意两个顶点会产生一个新的环;
- 从树中任意删除一条边将会得到两颗独立的树。
2.1 切分原理
图的一种切分是将图的所有顶点分为两个非空且不重叠的两个集合。横切边是一条连接两个属于不同集合的顶点的边。
通常我们通过指定一个顶点集隐式地认为它的补集为另外一个顶点集来指定一个切分。这样,一条横切边就是连接该集合的一个顶点和不在该集合中的另一个顶点的一条边。
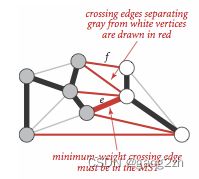
下图2.1-1所示为切分示意图:
命题J (切分定理)。在一幅加权图中,给定任意的切分,它的横切边中的权重最小者必然属于图的最小生成树。
证明:e为权重最小的横切边,T为图的最小生成树。我们采用反证法:假设T不包含e。那么将e加入T,得到的图形成一条经过e的环,且这个图中含有另外一条横切边-设为f,f的权重必然大于e(e为当前切分权重最小且图中所有边的权重不同)。那么我们删除掉f而保留e就得到一棵权重更小的生成树。这和我们的假设T矛盾。
- 权值最小的横切边并不一定是所有横切边中唯一属于图的最小生成树的边。
2.2 贪心算法
切分定理上解决最小生成树问题的所有算法的基础。更确切的说,这些算法都是一种贪心算法的特殊情况:使用切分定理找到最小生成树的一条边,不断重复直到找到最小生成树的所有边。这些算法相互之间不同之处在于保存切分和判定权重最小横切边的方式,但它们都是以下性质的特殊情况。
命题K(最小生成树的贪心算法)。下面这种方法会将含有V个顶点的任意加权连通图中属于最小生成树的边标记为黑色:初始状态下所有边均为黑色,找到一种切分,它产生的横切边均不为黑色。将它权重最小的横切边标记为黑色。反复,直到标记了V-1条黑色边为止。
证明:我们假设所有边权重不同,没有这个假设该命题同样成立。根据切分定理,所有被标记为黑色的边均属于最小生成树。如果黑色边的数量少于V-1,比如还存在不会产生黑色边的切分(因为我们假设图是连通的)。只要找到了V-1条黑色的边,这些边所组成的就是一棵最小生成树。
3 加权无向图数据类型
3.1 带权重的边的数据类型
加权无向图,为了能够使程序适用于更加常见的场景,我们把边单独抽象为一个类,加权边的API如下表3.1-1所示:
| 权限修饰符 返回值类型 | 类名或者方法名 | 描述 |
|---|---|---|
| public class | Edge | 加权边 |
| public | Edge(int v, int w, double weight) | 初始化构造函数 |
| public double | weight() | 边的权重 |
| public int | either() | 边两端的顶点之一 |
| public int | other(int v) | 另一个顶点 |
| public String | toString() | 对象的字符串表示 |
加权边的源代码,取自《算法第四版》,如下所示:
package edu.princeton.cs.algs4;
/**
* 加权边
*/
public class Edge implements Comparable<Edge> {
private final int v;
private final int w;
private final double weight;
/**
* 初始化边v-w,权重weight
*/
public Edge(int v, int w, double weight) {
if (v < 0) throw new IllegalArgumentException("vertex index must be a non-negative integer");
if (w < 0) throw new IllegalArgumentException("vertex index must be a non-negative integer");
if (Double.isNaN(weight)) throw new IllegalArgumentException("Weight is NaN");
this.v = v;
this.w = w;
this.weight = weight;
}
/**
* 边的权重
*/
public double weight() {
return weight;
}
/**
* 边的其中一个顶点
*/
public int either() {
return v;
}
/**
* 边的另外一个顶点
*/
public int other(int vertex) {
if (vertex == v) return w;
else if (vertex == w) return v;
else throw new IllegalArgumentException("Illegal endpoint");
}
/**
* 比较两条边
*/
@Override
public int compareTo(Edge that) {
return Double.compare(this.weight, that.weight);
}
/**
* 边的字符串表示
*/
public String toString() {
return String.format("%d-%d %.5f", v, w, weight);
}
}
3.2 加权无向图的数据结构
加权无向图API如下表3.2-1所示:
| 权限修饰符 返回值类型 | 类名或者方法名 | 描述 |
|---|---|---|
| public class | EdgeWeightedGraph | 加权无向图 |
| public | EdgeWeightedGraph(itn v) | 创建一幅含有v个顶点的空图 |
| public | EdgeWeightedGraph(In in) | 从输入流读取图 |
| public int | V() | 图的顶点数 |
| public int | E() | 图的边数 |
| public void | addEdge(Edge e) | 向图中添加一条边e |
| public Iterable |
adj(int v) | v的邻接表 |
| public Iterable |
edges() | 图的所有边 |
| public String | toString() | 图的字符串表示 |
加权无向图的源代码如下3.2-1所示:
package edu.princeton.cs.algs4;
import java.util.NoSuchElementException;
/**
* 加权无向图
*/
public class EdgeWeightedGraph {
private static final String NEWLINE = System.getProperty("line.separator");
/**
* 顶点数
*/
private final int V;
/**
* 边数
*/
private int E;
/**
* 邻接表
*/
private Bag<Edge>[] adj;
/**
* 初始化含有V个顶点的空图
*/
public EdgeWeightedGraph(int V) {
if (V < 0) throw new IllegalArgumentException("Number of vertices must be non-negative");
this.V = V;
this.E = 0;
adj = (Bag<Edge>[]) new Bag[V];
for (int v = 0; v < V; v++) {
adj[v] = new Bag<Edge>();
}
}
/**
* 从输入流读取一幅图
*/
public EdgeWeightedGraph(In in) {
if (in == null) throw new IllegalArgumentException("argument is null");
try {
V = in.readInt();
adj = (Bag<Edge>[]) new Bag[V];
for (int v = 0; v < V; v++) {
adj[v] = new Bag<Edge>();
}
int E = in.readInt();
if (E < 0) throw new IllegalArgumentException("Number of edges must be non-negative");
for (int i = 0; i < E; i++) {
int v = in.readInt();
int w = in.readInt();
validateVertex(v);
validateVertex(w);
double weight = in.readDouble();
Edge e = new Edge(v, w, weight);
addEdge(e);
}
}
catch (NoSuchElementException e) {
throw new IllegalArgumentException("invalid input format in EdgeWeightedGraph constructor", e);
}
}
/**
* 深拷贝一幅加权无向图
*/
public EdgeWeightedGraph(EdgeWeightedGraph G) {
this(G.V());
this.E = G.E();
for (int v = 0; v < G.V(); v++) {
// reverse so that adjacency list is in same order as original
Stack<Edge> reverse = new Stack<Edge>();
for (Edge e : G.adj[v]) {
reverse.push(e);
}
for (Edge e : reverse) {
adj[v].add(e);
}
}
}
/**
* 图的顶点数
*/
public int V() {
return V;
}
/**
* 图的边数
*/
public int E() {
return E;
}
/**
* 校验顶点v
*/
private void validateVertex(int v) {
if (v < 0 || v >= V)
throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
}
/**
* 添加一条边e
*/
public void addEdge(Edge e) {
int v = e.either();
int w = e.other(v);
validateVertex(v);
validateVertex(w);
adj[v].add(e);
adj[w].add(e);
E++;
}
/**
* 顶点v的邻接表
*/
public Iterable<Edge> adj(int v) {
validateVertex(v);
return adj[v];
}
/**
* 顶点v的度数
*/
public int degree(int v) {
validateVertex(v);
return adj[v].size();
}
/**
* 图中所有边
*/
public Iterable<Edge> edges() {
Bag<Edge> list = new Bag<Edge>();
for (int v = 0; v < V; v++) {
int selfLoops = 0;
for (Edge e : adj(v)) {
if (e.other(v) > v) {
list.add(e);
}
// add only one copy of each self loop (self loops will be consecutive)
else if (e.other(v) == v) {
if (selfLoops % 2 == 0) list.add(e);
selfLoops++;
}
}
}
return list;
}
/**
* 图的字符串表示
*/
public String toString() {
StringBuilder s = new StringBuilder();
s.append(V + " " + E + NEWLINE);
for (int v = 0; v < V; v++) {
s.append(v + ": ");
for (Edge e : adj[v]) {
s.append(e + " ");
}
s.append(NEWLINE);
}
return s.toString();
}
}
3.3 测试
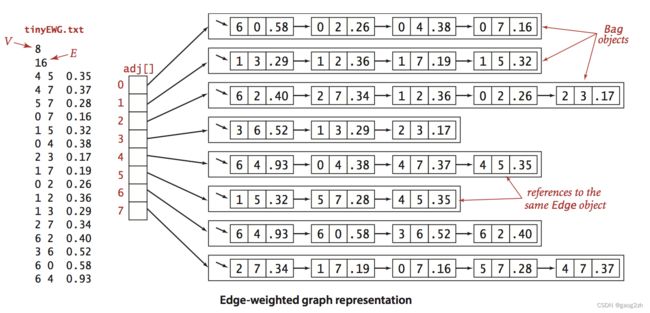
测试文件tinyEWG.txt,数据及存储结构如下图3.3-1所示:
结语
如果小伙伴什么问题或者指教,欢迎交流。
❓QQ:806797785
⭐️源代码仓库地址:https://gitee.com/gaogzhen/algorithm
参考链接:
[1][美]Robert Sedgewich,[美]Kevin Wayne著;谢路云译.算法:第4版[M].北京:人民邮电出版社,2012.10.p390-398.