学习通信原理之——从实验中理解频谱/功率谱/功率谱密度(MATLAB演示)

我的个人博客文章链接如下：学习通信原理之——从实验中理解频谱/功率谱/功率谱密度(MATLAB演示)

前言

最近在复习通信原理，每次到了功率谱这一块就感到困惑，每次都要去查，我觉得不能再这样循环下去了，这次一定要对这三个概念理解透彻，于是去网上找了资料去学习。

---

学习了b站视频：NO.31 十分钟搞定频谱/功率谱/功率谱密度
在这里记录下自己的一些感悟与理解

---

介绍

频谱

频谱是指某个信号在频域上的表示，即它在不同频率下的成分及其相对强度。在信号处理中，频谱常用于分析信号的频率内容和频率分布，可以用于音频、视频、无线通信等领域的分析和处理。频谱通常用图形方式表示，其中横轴表示频率，纵轴表示信号在该频率上的强度或功率，可以是线性或对数坐标。

功率谱

功率谱表示单位频带内信号功率随频率的变化情况,单位是W，即它在不同频率下的功率或能量分布情况。与频谱类似，功率谱也是用于分析信号频率内容和频率分布的一种工具，但它考虑的是信号在不同频率下的功率或能量分布，因此可以更直观地描述信号的能量分布情况。通常，功率谱的横坐标是频率，纵坐标是功率或能量密度，可以是线性或对数坐标。功率谱在很多领域都有广泛的应用，比如无线通信、音频信号处理、图像处理等。

功率谱密度

功率谱密度表示单位时间和单位频带内信号能量随频率的分布情况，单位是能量除时间除频带，通常用于描述信号在连续频域上的功率分布情况。与功率谱类似，功率谱密度也是描述信号在不同频率下的功率或能量分布情况，但它考虑的是单位频率范围内的功率或能量分布情况，因此它可以更精确地描述信号的功率分布情况，尤其是对于带宽非常宽的信号而言。功率谱密度通常用于分析连续时间信号或随机信号的频率特性，比如噪声、振动、电磁干扰等。功率谱密度的单位通常是功率或能量密度除以频率单位，例如瓦特/赫兹（W/Hz）或焦耳/赫兹（J/Hz）。

---

由电路中的功率想到信号功率

$$电路中的功率:P=\frac{V^2}{R}=I^{2}R$$

若

$$R=1\Omega$$

$$电路中的功率:P=V^2=I^2$$

如果将V 换成信号的序列s(t)，我们能发现，我们所说的功率谱公式，就是来源上面的公式。

---

计算信号能量和能量谱密度

那么这个信号自产生到结束的总能量就是
$$E={\int }_{-\infty }^{+\infty }s(t{)}^{2}dt={\int }_{-\infty }^{+\infty }{\left|S(f)\right|}^{2}df$$
E存在，即称为能量信号;
能量谱密度：

$$G(f)={\left|s(f)\right|}^2,J/HZ$$

计算信号功率和功率谱密度

因为功率信号的能量是无限的，所以我们只取-T/2~T/2,来计算其功率

E T = ∫ − T 2 T 2 s T ( t ) 2 d t = ∫ − ∞ ∞ ∣ S T ( f ) 2 ∣ d f E_{T}=\int_{-\frac{T}{2} }^{\frac{T}{2} } s_{T}(t)^2 dt=\int_{-\infty }^{\infty }\left | S_{T}(f)^2 \right | df ET​=∫−2T​2T​​sT​(t)2dt=∫−∞∞​ ​ST​(f)2 ​df

$$P(f)=\underset{T\to \infty }{\lim }\frac{1}{T}{\left|S(f)\right|}^2$$
P(f)就是功率谱密度
功率信号的功率P就是：
$$P=\underset{T\to \infty }{\lim }\int {\left|S(f)\right|}^{2}df={\int }_{-\infty }^{\infty }P(f)df$$
P存在，即称为功率信号
由上面的式子可知：

时域信号傅立叶变换模平方然后除以时间长度（来自能量谱密度）。 根据帕塞瓦尔定理，信号傅立叶变换模平方被定义为能量谱，能量谱密度在时间上平均就得到了功率谱。功率谱密度P(f)在频率轴上积分，T趋向无穷大，就是信号的功率P。

总结：

能量有限、功率为零的信号为能量信号。

能量无限、功率有限的信号为功率信号。

所有周期信号都是功率信号；所有有限数量的脉冲信号都是能量信号。

---

MATLAB画一个随机信号的频谱

生成随机信号

%生成随机信号
noiseLevel=2;
signal = rand(80000,1);
noise = randn(80000,1) * noiseLevel;
signal = signal + noise;

做傅立叶变换并画图

X = signal;
Fs = 2e3;
L = length(X);
Y = fft(X);%傅立叶变换
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1)=2*P1(2:end-1);
f = Fs*(0:(L/2))/L;
%频谱
%subplot(231);
plot(f,P1);
ylim([0 0.05]);
title('频谱');
xlabel('f(Hz)');
ylabel('|P1(f)|(单位:mV)');

因为没有进行任何的滤波等操作，所以里面的直流分量、噪声等影响因素都存在，这就是一个很完全的原始信号。

MATLAB画这个随机信号的功率谱

功率实际上就是能量的平方。
为了便于观察功率谱的变化，我们对横坐标的功率化成了dBm
$$dBm=10lo{g}_{10}\frac{P}{1mW}$$

%功率谱
subplot(232);
plot(f,10*log10(P1.^2));%将W转为dBm
title('功率谱');
xlabel('f(Hz)');
ylabel('|P1(f)|^2(单位:dBm)');

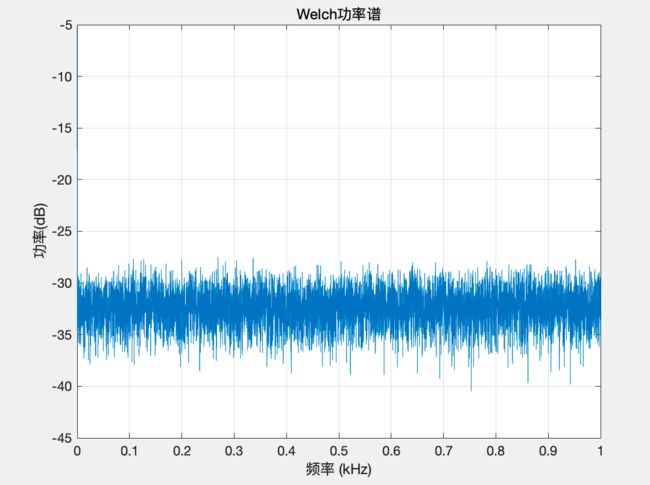
MATLAB画这个随机信号的功率谱(另一种方法)

%第二种方法求功率谱
pwelch(signal,[],[],[],Fs,'power');
title('Welch功率谱');

MATLAB画这个随机信号的功率谱密度

pwelch(signal,[],[],[],Fs);

功率谱密度纵轴的单位变成了(db/Hz)，表示每一个Hz有多少dB。
跟功率谱图像做对比，可以观察到，幅度较大的频率分量被保留了下来。

---

pwelch函数含义

pwelch是Matlab中用于计算功率谱密度的函数。它的基本语法是：

[Pxx,F] = pwelch(x,window,noverlap,nfft,fs)

其中，x是一个向量或矩阵，表示要计算功率谱密度的信号，window是窗函数，noverlap是窗函数之间的重叠部分，nfft是FFT的点数，fs是采样率。函数将返回一个功率谱密度估计值向量Pxx和一个对应的频率向量F。

完整代码

clear
close all
clc

%生成随机信号
noiseLevel=2;
signal = rand(80000,1);
noise = randn(80000,1) * noiseLevel;
signal = signal + noise;

X = signal;
Fs = 2e3;
L = length(X);
Y = fft(X);%傅立叶变换
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1)=2*P1(2:end-1);
f = Fs*(0:(L/2))/L;
%频谱
subplot(221);
plot(f,P1);
ylim([0 0.05]);
title('频谱');
xlabel('f(Hz)');
ylabel('|P1(f)|(单位:mV)');
%功率谱
subplot(222);
plot(f,10*log10(P1.^2));%将W转为dBm
title('功率谱');
xlabel('f(Hz)');
ylabel('|P1(f)|^2(单位:dBm)');
%第二种方法求功率谱
subplot(223);
pwelch(signal,[],[],[],Fs,'power');
title('Welch功率谱');
%功率谱密度
subplot(224);
pwelch(signal,[],[],[],Fs);