实验七-卷积编码的MATLAB实现
信息论编码实验3~9连载，更多看专栏。
实验七-卷积编码的MATLAB实现
- 一、卷积码原理介绍
-
- 1.1 基本概念
- 1.2 (n,k,N)卷积编码
-
- 1.2.1 编码
- 1.2.2 译码 - Viterbi 译码算法
- 二、代码展示及运行结果
-
- 2.1 (2,1,3)卷积码编码
- 2.2 (2,1,3)卷积码解码
- 2.3 (2,1,3)卷积码性能探究
-
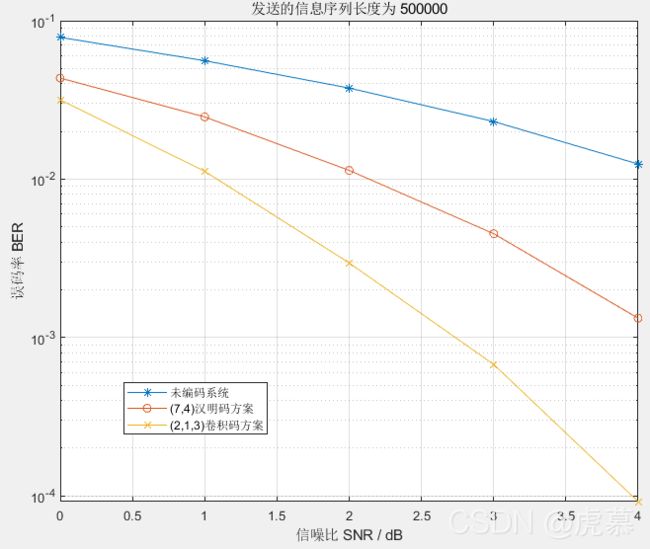
- 2.3.1. 未编码系统、(7,4)汉明编码系统、(2,1,3)卷积编码系统 的对比：
- 2.3.2 未编码系统、(2,1,3)卷积编码系统、(2,1,5)卷积编码系统 的对比：
- 2.3.3 未编码系统、(2,1,3)卷积编码系统、(3,1,3)卷积编码系统 的对比：
- 三、程序自评价
- 附录
一、卷积码原理介绍
1.1 基本概念
基本概念可以参考实验六的文章。
1.2 (n,k,N)卷积编码
1.2.1 编码
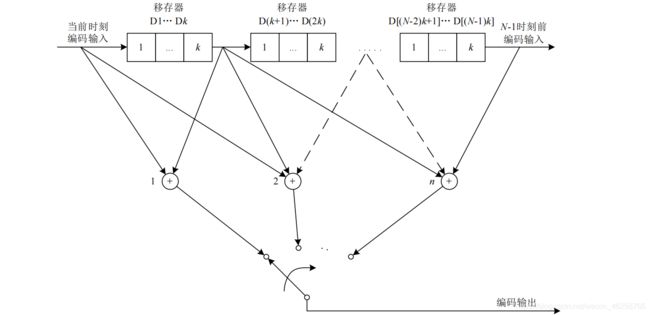上图是卷积编码的通用电路原理图。要看懂这个图需要明确几点概念：
- 编码器由三种主要元件构成，包括( N-1 ) k 级移存器、n 个模二加法（异或）器和一个旋转开关；
- 在每个时隙，旋转开关输出 n 位后回到原点，移存器的值集体向右挪 k 位（最左边移存器存入新输入的值）；
- 模二加法器的输入端不拘泥于上图所示，理论上可以取任意移存器任意值；
由于 k 只是决定了每一组寄存器的数量；以下，本文一直默认 k = 1。
由于在编写程序时，数据都存储在矩阵里，所以对上述实际通用原理图有如下改变：
- 直接从方框读取数据。
- 编码器包括N*k级移存器，用于存放所有数据。
好吧，我承认上面的理论我自己看了都烦，所以下面直接展示(2,1,3)卷积编码的原理图：
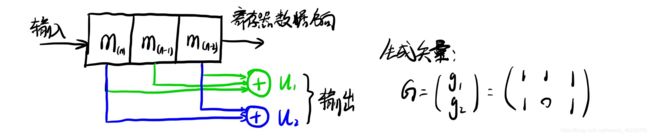异或器的输入端取决于生成矢量（如图右侧所示）。对于硬件电路来说，每个时钟周期到来时，从左侧高位输入一位数据，同时两个异或器输出两个数([u1,u2])。多简单明了！
当然，对于软件逻辑来说，就是每次循环先计算输出，然后将数据[mn,mn-1]移到[mn-1,mn-2]，然后更新[mn]。
另外，针对上述编码原理，实验指导书上给出了很多种的描述方法（见下图），下面只写出我认为最简洁的生成矩阵法。
卷积码原理描述方法
代数描述方式
1.生成矩阵法
2.生成矢量法
3.生成多项式法
几何描述方式
4.树图
5.状态转移图
注意，新输入的数据在最左端。可以看出：
n = 生成矢量的行数；
k = 每组数据包含寄存器的个数；
N = 生成矢量的列数；
于是对于每k(取值为1)个数据输入，有发送端输出：
U = [ u 1 , u 2 ] = [ m n , m n − 1 , m n − 2 ] ∗ G . ′ = M ∗ G . ′ U=[u_1,u_2] =[m_n,m_n-_1,m_n-_2]*G.'=M*G.' U=[u1,u2]=[mn,mn−1,mn−2]∗G.′=M∗G.′
有了这个公式下面就可以编码啦~
1.2.2 译码 - Viterbi 译码算法
译码原理有些复杂，B站有对应的视频“卷积码译码”搜索结果。
二、代码展示及运行结果
2.1 (2,1,3)卷积码编码
%% 测试主函数
clear all
clc
G = [1,0,1;1,1,1];
M = [1 1 0 0 1 0 1 1];
C = conv_encode(M,G);
% 展示卷积码
C_reshape = reshape(C,length(M)+3,2).';
%disp(C_reshape);
%disp(['(2,1,3)卷积码编码系统',num2str(C)]);
fprintf(' 输入序列：\t%s\n',num2str(M));
fprintf('卷积编码系统：\t%s\n',num2str(C_reshape));
%% 本函数实现卷积编码
function C = conv_encode(m,G)
%{
输入：
原始序列m
生成矢量G
输出：
卷积码结果C
特点：
适用于所有的[n,1,N]卷积编码
%}
len = length(m);
k=1; % 表示每次对k个码元进行编码
[n,N] = size(G);% n表示一个输入码元拥有几个输出，N表示每次监督的输入码元数
C = zeros(1,n*len);
% 在头尾补0，方便卷积输出和寄存器清洗
m_add0 = [zeros(1,N-1),m,zeros(1,N+1)];
% 循环每一位输入符号，获得输出矩阵
C_reg = fliplr(m_add0(1,1:N));
for i =1:len+N
%生成每一位输入符号的n位输出
C(n*i-(n-1):n*i) = mod(C_reg*G.',2);
%更新寄存器序列+待输出符号（共N个符号）
C_reg = [m_add0(i+N),C_reg];% 添加新符号
C_reg(end) = [];% 挤掉旧符号
end
主函数运行结果如下：
2.2 (2,1,3)卷积码解码
为了减负，老师直接下放了解码代码，而且注释十分详尽（我没啥可以补充的），所以就放到最后的附录了。
2.3 (2,1,3)卷积码性能探究
以下都结合了老师给的卷积译码函数。
2.3.1. 未编码系统、(7,4)汉明编码系统、(2,1,3)卷积编码系统 的对比：
条件是AWGN信道BPSK调制。
下面这个函数调用的自定义子函数有：“hamming”、“ham_decode”、“BPSK_AWGN”（这三个都放在下面了），“conv_encode”（在上面），子函数为“conv_decode”是老师给的就不放了。
%% 实验七-（AWGN信道BPSK调制）未编码系统、(7,4)汉明码、(2,1,3)卷积码的BER-SNR对比
clear all
clc
%% 主函数
N = input('每个信噪比条件下要发送多少个样本点：');
snrdB_min = 0; snrdB_max = 4;% SNR范围是0-4dB
snrdB = snrdB_min:1:snrdB_max;
sym_initial = round(rand(1,N));% 生成原始序列
% 获得(7,4)汉明码编码C_hamming
G_ham = [1 0 0 0 1 1 0;...
0 1 0 0 1 0 1;...
0 0 1 0 0 1 1;...
0 0 0 1 1 1 1]; % 生成矩阵G
[k1,n1] = size(G_ham);
C_ham = hamming(sym_initial,G_ham);
[groups1,~] = size(C_ham);
C_ham_stream = reshape(C_ham.',[1,length(C_ham(:))]);% 转换成码流
% 获得(2,1,3)卷积码C_conv
G_conv = [1,0,1;1,1,1];
C_conv_stream = conv_encode(sym_initial,G_conv);
% 若想展示输出，建议用C_conv
%C_conv = reshape(C_conv_stream,length(sym_initial)+3,2).';
%fprintf('卷积编码系统：\t%s\n',num2str(C_conv));
% 三种序列都在AWGN信道下，进行BPSK调制解调，得到接收端接收序列
[~,BER_dir] = BPSK_AWGN(sym_initial,snrdB);% 直接发送原始码流
[RX_ham,~] = BPSK_AWGN(C_ham_stream,snrdB);% 发送汉明码调制码流
[RX_conv,~] = BPSK_AWGN(C_conv_stream,snrdB);% 发送卷积码码流
% 汉明码解码并计算SNR
errors_ham = zeros(1,length(snrdB)); % 预分配错误内存
for i=1:length(snrdB)
RX_ham1 = reshape(RX_ham(i,:),[n1,groups1]).';
result_ham = ham_decode(RX_ham1,G_ham);% 解码
errors_ham(i) = sum(sum(mod(result_ham+C_ham(:,1:k1),2)));
end
BER_ham = errors_ham/N; % 得到BER
% 卷积码解码并计算SNR
errors_conv = zeros(1,length(snrdB)); % 预分配错误内存
for i=1:length(snrdB)
[result_conv] = conv_decode(G_conv,1,RX_conv(i,:));% 解码
errors_conv(i) = sum(mod(result_conv+sym_initial,2));
end
BER_conv = errors_conv/N; % 得到BER
% 画出三种方案的BER-SNR曲线
figure
semilogy(snrdB,BER_dir,'*-',snrdB,BER_ham,'o-',snrdB,BER_conv,'-x');
grid on;
xlabel('信噪比 SNR / dB');ylabel('误码率 BER');
title(['发送的信息序列长度为 ',num2str(N)]);
legend('未编码系统','(7,4)汉明码方案','(2,1,3)卷积码方案');
% 直接显示数值
disp(['未编码系统',num2str(BER_dir)]);
disp(['汉明码系统',num2str(BER_ham)]);
disp(['卷积码系统',num2str(BER_conv)]);
% 子函数-汉明码编码
function C = hamming(M,G)
%{
输入：
原始序列M
生成矩阵G
输出：
汉明编码比特流C
%}
[k,n] = size(G);
% 输入序列补位
N = size(M,2); % 获得输入序列元素个数
r = mod(-rem(N,k),k); % 获得需要对输入序列进行补位的个数
M_add0 = [M,zeros(1,r)];% 补位
% 将输入信息序列进行分组
groups = ceil(length(M_add0)/k); % 获得分组个数
M_dis = reshape(M_add0,[k,groups]).';
% 生成编码结果C
C = mod(M_dis*G,2);% 生成结果别忘了对2取余
end
% 子函数-汉明码解码
function C_result = ham_decode(R,G)
%{
输入：
接收序列R
生成矩阵G
输出：
译码结果C_result
%}
[k,n] = size(G);
% 根据G生成校验矩阵
H = [G(:,k+1:n).',[1 0 0;0 1 0;0 0 1]];
% 生成伴随式S
S = mod(R*(H.'),2);
[S_row,S_column] = size(S);
% 设置伴随式和错误图样的对应元胞矩阵
SE = {[0 0 0],[0 0 0 0 0 0 0];...
[0 0 1],[0 0 0 0 0 0 1];...
[0 1 0],[0 0 0 0 0 1 0];...
[1 0 0],[0 0 0 0 1 0 0];...
[1 1 1],[0 0 0 1 0 0 0];...
[0 1 1],[0 0 1 0 0 0 0];...
[1 0 1],[0 1 0 0 0 0 0];...
[1 1 0],[1 0 0 0 0 0 0]};
% 找出计算出的伴随式所对应的错误图样，并进行纠正
C_result = zeros(S_row,n);
[SE_row,SE_column] = size(SE);
for m=1:S_row
for n=1:SE_row
if all(S(m,:) == cell2mat(SE(n,1)))
C_result(m,:) = R(m,:)+cell2mat(SE(n,2));
C_result(m,:) = mod(C_result(m,:),2);
end
end
end
C_result = C_result(:,1:k);
end
% 子函数-BPSK调制（AWGN信道）
function [RX,BER] = BPSK_AWGN(TX,SNR)
%{
输入：
原始码元序列Tx
信噪比范围SNR(dB)
输出：
接收判别后序列RX,每一行代表一个信噪比的情况
信噪比对应的误码率序列BER
%}
N = length(TX); % 获得原始序列长度
snr = 10.^(SNR/10); % 转化成公制
len_snr = length(snr); % 获得SNR范围长度
RX = zeros(len_snr,N); % 预分配接收判别序列内存
errors = zeros(1,len_snr); % 预分配错误内存
for j=1:len_snr % 遍历所有SNR
sigma = sqrt(1/(2*snr(j))); % 计算SNR下AWGN的标准差
error_count = 0;
for i=1:N % 遍历每一个发送符号
x_d = 2*TX(i) - 1; % 得到+1和-1的发送序列
n_d = sigma*randn(1); % GWN
y_d = x_d + n_d; % 加性噪声
if y_d > 0
RX(j,i) = 1;
else
RX(j,i) = 0;
end
if (RX(j,i) ~= TX(i))
error_count = error_count + 1; % 对错误样本进行计数
end
end
errors(j) = error_count; % 得到该信噪比下的错误个数
end
BER = errors/N; % BER estimate
end
2.3.2 未编码系统、(2,1,3)卷积编码系统、(2,1,5)卷积编码系统 的对比：
条件是AWGN信道BPSK调制。
自定义子函数包括“BPSK_AWGN”、“conv_encode”、“conv_decode”。
%% 实验七-（AWGN信道BPSK调制）未编码系统、(2,1,3)卷积码、(2,1,5)卷积码的BER-SNR对比
clear all
clc
%% 主函数
N = input('每个信噪比条件下要发送多少个样本点：');
snrdB_min = 0; snrdB_max = 4;% SNR范围是0-4dB
snrdB = snrdB_min:1:snrdB_max;
sym_initial = round(rand(1,N));% 生成原始序列
% 获得(2,1,3)卷积码C_conv
G_conv1 = [1,0,1;1,1,1];
C_conv_stream1 = conv_encode(sym_initial,G_conv1);
% 若想展示输出，建议用C_conv
%C_conv1 = reshape(C_conv_stream1,length(sym_initial)+3,2).';
%fprintf('卷积编码系统：\t%s\n',num2str(C_conv1));
% 获得(2,1,5)卷积码C_conv
G_conv2 = [1,0,0,1,1;1,1,1,0,1];
C_conv_stream2 = conv_encode(sym_initial,G_conv2);
% 若想展示输出，建议用C_conv
%C_conv2 = reshape(C_conv_stream2,length(sym_initial)+5,2).';
%fprintf('卷积编码系统：\t%s\n',num2str(C_conv2));
% 三种序列都在AWGN信道下，进行BPSK调制解调，得到接收端接收序列
[~,BER_dir] = BPSK_AWGN(sym_initial,snrdB);% 直接发送原始码流
[RX_conv1,~] = BPSK_AWGN(C_conv_stream1,snrdB);% 发送(213)卷积码码流
[RX_conv2,~] = BPSK_AWGN(C_conv_stream2,snrdB);% 发送(215)卷积码码流
% (213)卷积码解码并计算SNR
errors_conv1 = zeros(1,length(snrdB)); % 预分配错误内存
for i=1:length(snrdB)
result_conv1 = conv_decode(G_conv1,1,RX_conv1(i,:));% 解码
errors_conv1(i) = sum(mod(result_conv1+sym_initial,2));
end
BER_conv1 = errors_conv1/N; % 得到BER
% (215)卷积码解码并计算SNR
errors_conv2 = zeros(1,length(snrdB)); % 预分配错误内存
for i=1:length(snrdB)
result_conv2 = conv_decode(G_conv2,1,RX_conv2(i,:));% 解码
errors_conv2(i) = sum(mod(result_conv2+sym_initial,2));
end
BER_conv2 = errors_conv2/N; % 得到BER
% 画出三种方案的BER-SNR曲线
figure
semilogy(snrdB,BER_dir,'*-',snrdB,BER_conv1,'o-',snrdB,BER_conv2,'-x');
grid on;
xlabel('信噪比 SNR / dB');ylabel('误码率 BER');
title(['发送的信息序列长度为 ',num2str(N)]);
legend('未编码系统','(2,1,3)卷积码方案','(2,1,5)卷积码方案');
% 直接显示数值
disp(['未编码系统',num2str(BER_dir)]);
disp(['(213)卷积码系统',num2str(BER_conv1)]);
disp(['(215)卷积码系统',num2str(BER_conv2)]);
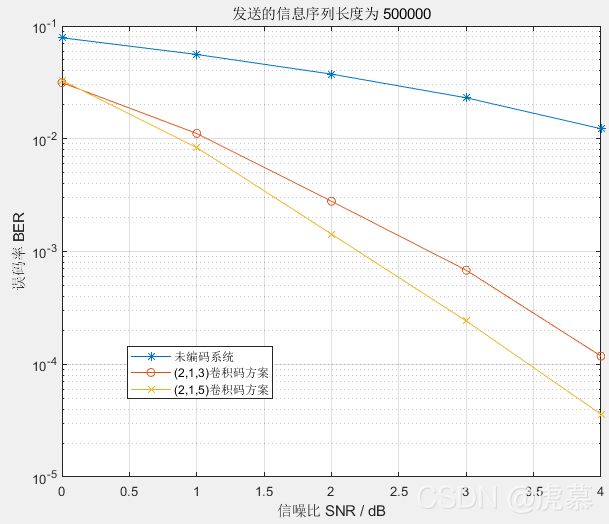
以下是我自己的猜想：
根据上图，在低信噪比下，(2,1,5)卷积码的性能比(2,1,3)卷积码要差，但是当信噪比高于某一阈值之后，情况相反。
初步推测，由于译码时是根据接收的序列猜测正确概率最大的那一个。当信噪比较低时错误的比特数较多，译码时每一种可能都相差不多（都很高），所以增加约束长度反而会增加选到错误路径的概率；但是在高信噪比的情况下，正确路径的概率明显高于其他路径，这时增加约束长度，就能更准确的锁定正确的路径。
2.3.3 未编码系统、(2,1,3)卷积编码系统、(3,1,3)卷积编码系统 的对比：
条件是AWGN信道BPSK调制。
自定义子函数包括“BPSK_AWGN”、“conv_encode”、“conv_decode”。
%% 实验七-（AWGN信道BPSK调制）未编码系统、(2,1,3)卷积码、(3,1,3)卷积码的BER-SNR对比
clear all
clc
%% 主函数
N = input('每个信噪比条件下要发送多少个样本点：');
snrdB_min = 0; snrdB_max = 4;% SNR范围是0-4dB
snrdB = snrdB_min:1:snrdB_max;
sym_initial = round(rand(1,N));% 生成原始序列
% 获得(2,1,3)卷积码C_conv
G_conv1 = [1,0,1;1,1,1];
C_conv_stream1 = conv_encode(sym_initial,G_conv1);
% 若想展示输出，建议用C_conv
%C_conv1 = reshape(C_conv_stream1,length(sym_initial)+3,2).';
%fprintf('卷积编码系统：\t%s\n',num2str(C_conv1));
% 获得(3,1,3)卷积码C_conv
G_conv2 = [1,0,1;1,1,1;1,1,1];
C_conv_stream2 = conv_encode(sym_initial,G_conv2);
% 若想展示输出，建议用C_conv
%C_conv2 = reshape(C_conv_stream2,length(sym_initial)+3,3).';
%fprintf('卷积编码系统：\t%s\n',num2str(C_conv2));
% 三种序列都在AWGN信道下，进行BPSK调制解调，得到接收端接收序列
[~,BER_dir] = BPSK_AWGN(sym_initial,snrdB);% 直接发送原始码流
[RX_conv1,~] = BPSK_AWGN(C_conv_stream1,snrdB);% 发送(213)卷积码码流
[RX_conv2,~] = BPSK_AWGN(C_conv_stream2,snrdB);% 发送(313)卷积码码流
% (213)卷积码解码并计算SNR
errors_conv1 = zeros(1,length(snrdB)); % 预分配错误内存
for i=1:length(snrdB)
[result_conv] = conv_decode(G_conv1,1,RX_conv1(i,:));% 解码
errors_conv1(i) = sum(mod(result_conv+sym_initial,2));
end
BER_conv1 = errors_conv1/N; % 得到BER
% (313)卷积码解码并计算SNR
errors_conv2 = zeros(1,length(snrdB)); % 预分配错误内存
for i=1:length(snrdB)
[result_conv] = conv_decode(G_conv2,1,RX_conv2(i,:));% 解码
errors_conv2(i) = sum(mod(result_conv+sym_initial,2));
end
BER_conv2 = errors_conv2/N; % 得到BER
% 画出三种方案的BER-SNR曲线
figure
semilogy(snrdB,BER_dir,'*-',snrdB,BER_conv1,'o-',snrdB,BER_conv2,'-x');
grid on;
xlabel('信噪比 SNR / dB');ylabel('误码率 BER');
title(['发送的信息序列长度为 ',num2str(N)]);
legend('未编码系统','(2,1,3)卷积码方案','(3,1,3)卷积码方案');
% 直接显示数值
disp(['未编码系统',num2str(BER_dir)]);
disp(['(213)卷积码系统',num2str(BER_conv1)]);
disp(['(313)卷积码系统',num2str(BER_conv2)]);
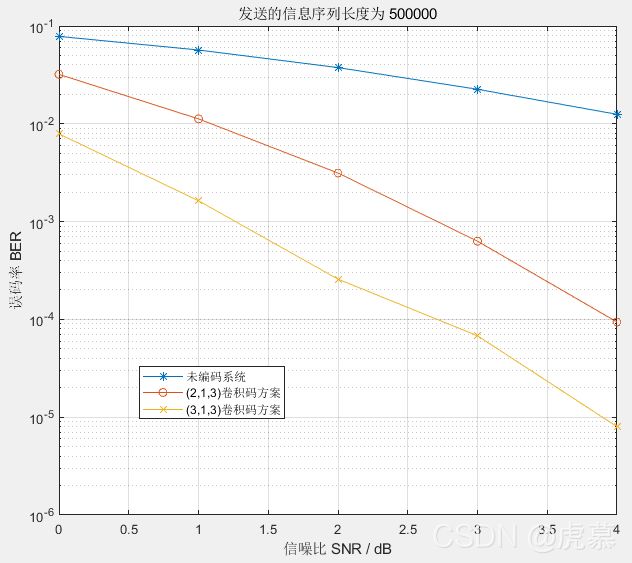
以下是我自己的猜想：
由于冗余码的增加是为保证可靠性。显然，(3,1,3)卷积码（码率33.3%）的冗余码肯定要多于(2,1,3)卷积码（码率50%），而两者原理相同，所以(3,1,3)卷积码以牺牲数据传输速率的方式显著提高了误码性能。
三、程序自评价
1.关于普适性。编码函数可以自动识别 n 和 N 的值，适用于所有的(n,1,N)卷积码，但是 k 的值默认为 1 不可调节。
2.关于分组。编码函数实现了程序内进行码流拼接（不像实验六），所以输入和输出都是码流，更加逼近真实情况。
代码原创，但因为原理编写参考到了实验课的指导书，假如有什么不对的地方，侵删。
附录
卷积码解码的代码：
function [ decode_output ] = conv_decode( g,k,decode_input )
% (n,k,L)卷积Viterbi译码器
% g n个生成矢量排列形成的卷积码生成矩阵:g = [g1;g2;...;gn]
% k 编码位数
% decode_input 输入码流
% 约束长度N
N = size(g,2);
% 编码输出位数n
n = size(g,1);
% 网格图的状态数
number_of_states = 2^(k*(N-1));
% 输入矩阵
input = zeros(number_of_states);
% 状态转移矩阵
nextstate = zeros(number_of_states,2^k);
% 输出矩阵
output = zeros(number_of_states,2^k);
%%%% 对各个状态进行运算，得到输入矩阵、状态转移矩阵与输出矩阵 %%%%
for s = 0:number_of_states-1
%对前一时刻状态到下一时刻状态之间的各条支路进行运算
for t = 0:2^k-1
% next_state_function函数产生移存器跳转到的下一状态及当前时刻编码器内容
[next_state,memory_contents] = next_state_function(s,t,N,k);
% 从上至下表示当前状态s0,s1,s2……
% 从左至右表示下一状态s0,s1,s2……
% 内容为经由支路编号
input(s+1,next_state+1) = t; %输入矩阵
% 各条支路编码输出
branch_output = rem(memory_contents*g',2);
% 从上至下表示当前状态s0,s1,s2……
% 从左至右为经由支路编号0,1,2……
% 内容为下一时刻状态s
nextstate(s+1,t+1) = next_state; %状态转移矩阵
% 从上至下表示当前状态s0,s1,s2……
% 从左至右表示经由支路编号0,1,2……
% 内容为相应分支输出编码
output(s+1,t+1) = bin2dec(branch_output); %输出矩阵
end
end
%%%%%%%%%%%%% 开始译码，得到幸存状态矩阵 %%%%%%%%%%%%%
% 状态度量矩阵
% 第一列为当前时刻各状态的路径度量
% 第二列为下一时刻各状态的路径度量（即更新后的状态度量）
state_metric = zeros(number_of_states,2);
% 网格深度
depth_of_trellis = length(decode_input)/n;
decode_input_matrix = reshape(decode_input,n,depth_of_trellis);
% 幸存状态矩阵
survivor_state = zeros(number_of_states,depth_of_trellis+1);
% 各个状态的初始路径度量
for i =1:N-1
% 网格图从全零状态出发，直到所有状态都有路径到达
for s = 0:2^(k*(N-i)):number_of_states-1
%对前一时刻状态到下一时刻状态之间的各条分支进行运算
for t = 0:2^k-1
% 分支度量
branch_metric = 0;
% 将各分支的编码输出以二进制形式表示
bin_output = dec2bin(output(s+1,t+1),n);
for j = 1:n
% 分支度量的计算
branch_metric = branch_metric + metric_hard(decode_input_matrix(j,i),bin_output(j));
end
% 各个状态路径度量值的更新
% 下一时刻路径度量=当前时刻路径度量+分支度量
state_metric(nextstate(s+1,t+1)+1,2) = state_metric(s+1,1) + branch_metric;
% 幸存路径的存储
% 一维坐标表示下一时刻状态
% 二维坐标表示该状态在网格图中的列位置
% 内容为当前时刻状态
survivor_state(nextstate(s+1,t+1)+1,i+1) = s;
end
end
% 对所有状态完成一次路径度量值计算后
% 状态度量矩阵第一列（当前状态路径度量）
% 与第二列（下一状态路径度量）对换
% 方便下一时刻继续迭代更新
state_metric = state_metric(:,2:-1:1);
end
% 各个状态的路径度量更新
for i = N:depth_of_trellis-(N-1)
% 记录某一状态的路径度量是否更新过
flag = zeros(1,number_of_states);
for s = 0:number_of_states-1
for t = 0:2^k-1
branch_metric = 0;
bin_output = dec2bin(output(s+1,t+1),n);
for j = 1:n
branch_metric = branch_metric + metric_hard(decode_input_matrix(j,i),bin_output(j));
end
% 若某状态的路径度量未被更新
% 或一次更新后的路径度量大于本次更新的路径度量
% 则进行各状态路径度量值的更新
if((state_metric(nextstate(s+1,t+1)+1,2)>state_metric(s+1,1)+branch_metric) || flag(nextstate(s+1,t+1)+1) == 0)
state_metric(nextstate(s+1,t+1)+1,2) = state_metric(s+1,1)+ branch_metric;
survivor_state(nextstate(s+1,t+1)+1,i+1) = s;
% 一次更新后flag置为1
flag(nextstate(s+1,t+1)+1) = 1;
end
end
end
state_metric = state_metric(:,2:-1:1);
end
% 结尾译码：网格图回归全零状态
for i = depth_of_trellis-(N-1)+1:depth_of_trellis
flag = zeros(1,number_of_states);
%上一比特存留的状态数
last_stop_states = number_of_states/(2^((i-depth_of_trellis+N-2)*k));
% 网格图上的各条路径最后都要回到同一个全零状态
for s = 0:last_stop_states-1
branch_metric = 0;
bin_output = dec2bin(output(s+1,1),n);
for j = 1:n
branch_metric = branch_metric+ metric_hard(decode_input_matrix(j,i),bin_output(j));
end
if((state_metric(nextstate(s+1,1)+1,2) > state_metric(s+1,1)+branch_metric) || flag(nextstate(s+1,1)+1) == 0)
state_metric(nextstate(s+1,1)+1,2) = state_metric(s+1,1)+ branch_metric;
survivor_state(nextstate(s+1,1)+1,i+1) = s;
flag(nextstate(s+1,1)+1) = 1;
end
end
state_metric = state_metric(:,2:-1:1);
end
%%%%%% 根据幸存状态矩阵开始逐步向前回溯，得到译码输出 %%%%%%%
sequence = zeros(1,depth_of_trellis+1);
% 逐步向前回溯
for i = 1:depth_of_trellis
sequence(1,depth_of_trellis+1-i) = survivor_state(sequence(1,depth_of_trellis+2-i)+1,depth_of_trellis+2-i);
end
% 译码输出
decode_output_matrix = zeros(k,depth_of_trellis-N);
for i = 1:depth_of_trellis-N
% 由输入矩阵得到经由支路编号
dec_decode_output = input(sequence(1,i)+1,sequence(1,i+1)+1);
% 将支路编号转为二进制码元，即为相应的译码输出
bin_decode_output = dec2bin(dec_decode_output,k);
% 将每一分支的译码输出存入译码输出矩阵中
decode_output_matrix(:,i) = bin_decode_output(k:-1:1)';
end
% 重新排列译码输出序列
decode_output = reshape(decode_output_matrix,1,k*(depth_of_trellis-N));
end
上述译码代码会用到的四个子函数：
function [ next_state,memory_contents ] = next_state_function( current_state,input,L,k )
%（n,k,L）编码,寄存器下一时刻状态跳转及当前时刻内容
% current_state 当前寄存器状态(DEC)
% input 编码输入（DEC），即分支编号
% L 约束长度
% k 编码位数
% next_state 下一时刻寄存器状态(DEC)
% memory_contents 当前时刻寄存器内容（BIN）
bin_current_state = dec2bin(current_state,k*(L-1));
bin_input = dec2bin(input,k);
bin_next_state = [bin_input,bin_current_state(1:k*(L-2))];
next_state = bin2dec(bin_next_state);
memory_contents = [bin_input,bin_current_state];
end
function [ distance ] = metric_hard( x,y )
% 硬判决与汉明距测量
if x == y
distance = 0;
else
distance = 1;
end
end
function [ y ] = dec2bin( x,L )
% 十进制数转为二进制数
% x 十进制数
% y 二进制数
% L 二进制数长度
y = zeros(1,L);
i = 1;
while x>=0 && i<=L
y(i) = rem(x,2);
x = (x-y(i))/2;
i = i+1;
end
y = y(L:-1:1);
end
function [ y ] = bin2dec( x )
% 二进制数转为十进制数
% x 二进制数
% y 十进制数
L = length(x);
y = (L-1:-1:0);
y = 2.^y;
y = x*y';
end