深入理解MySQL索引底层数据结构

MySQL 索引相关的数据结构有两种，一种是 B+tree，一种是 Hash，那么为什么在 99.99% 的情况下都使用的是 B+tree索引呢？

索引的底层数据结构是怎样的呢？

接下来就听十一娓娓道来。

一、索引是什么

MySQL 官方对索引的定义：索引是帮助 MySQL 高效获取数据的排好序的数据结构。所以，可以得出：索引是数据结构！

当然啦，上面两句话可能看起来很抽象，那么生活中有哪些索引的例子呢。

可以看到，索引其实就是是一棵倒挂着的树，是一种数据结构。

同时附上一个可视化数据结构网站，有了它学习数据结构简单明了。

二、二叉树系列

先来简单说一说和 B+tree 相关的二叉树系列：二叉树、二叉查找树和平衡二叉树

#1. 二叉树

什么是二叉树嘞？

每个节点至多只有二棵子树，左子树和右子树，次序不能颠倒。逻辑上二叉树有五种基本形态：空二叉树、只有一个根结点的二叉树、只有左子树、只有右子树、完全二叉树(特例为满二叉树)。遍历是对树的一种最基本的运算，所谓遍历二叉树，就是按一定的规则和顺序走遍二叉树的所有结点，使每一个结点都被访问一次，而且只被访问一次，有前序、中序、后序遍历。

由于数据库索引是要求排好序的数据结构，所以二叉树是不满足使用场景的，那么为了解决排好序这个问题，那么就引出了二叉查找树。

#2. 二叉查找树

什么是二叉查找树嘞？

二叉查找树又名二叉搜索树，在满足二叉树的条件下，左子树的节点值总是小于根的节点值，右子树的节点值总是大于根的节点值，也就是左子树节点值 < 根的节点值 < 右子树节点值。

如下图的设计，将一组数据转化为二叉查找树，设计合理的二叉查找树查找一个节点数据时间复杂度和二分查找一样。

但是如果设计不合理会设计成什么样子呢？

设计不良极不平衡时，二叉搜索树甚至会变成顺序查找，而不是二分查找，如下图所示，同样一个数组最后设计出来的二叉查找树。

可以看到，在查找69和这个数据时，在第一张图中，构建合理的二叉查找树只需要2次 IO 就能找到数据；而第二张图中，构建出来的极不平衡二叉查找树需要 6 次磁盘 IO 才能找到数据。

所以，二叉搜索树解决了数据库索引排好序的原则，但是二叉查找树构建可能极不平衡，最后构建成了一个链表，这时候就需要用到平衡二叉树了，也就是我们平常说的 AVL树。

#3. 平衡二叉树(AVL树)

什么是平衡二叉树嘞？

首先符合二叉查找树的定义，其次必须满足任何节点的两个子树的高度之差的绝对值不超过 1。

上面这句话就很好理解了，也就是说在这个条件下保证了二叉查找树的平衡性，类似于下图结构。

平衡二叉树相比于二叉查找树来说，查找效率更稳定，总体的查找速度也更快。

平衡二叉树的查询速度的确很快，但是维护一棵平衡二叉树的代价是非常大的。通常来说，需要1次或多次左旋和右旋来得到插入、更新和删除后树的平衡性。

同时平衡二叉树随着数据的增多，平衡二叉树树的高度会越来越高，大概1000条数据就有9 - 10层，那也就是说可能找一个数据需要9 -10次 IO。

一般来说，一般的机械磁盘每秒至少可以做100次 IO，一次 IO 的时间基本上在0.01秒，也就是说1000条数据在查找时就需要0.1秒，那如果是10000条，1000000条呢。

所以，为了解决平衡二叉树高度过高导致的 IO 问题，提出了 B-tree 和 B+tree 数据结构。

#三、B-tree和B+tree

为了解决平衡二叉树高度过高导致的 IO 问题，于是想了个办法，能不能在每一个节点上多放些元素呢，从而降低平衡二叉树的高度，减少磁盘 IO，所以就有了 B-tree 和 B+tree。

#1. B-tree(B树)

B-tree 怎么定义呢？

B-tree 是一种多路搜索树，一棵 m 阶的 B-Tree 有如下特性：

每个节点最多有 m 个孩子。若根节点不是叶子节点，则至少有 2 个孩子。除了根节点和叶子节点外，其它每个节点至少有 Ceil(m/2) 个孩子。每个非叶子结点节点包含 n 个关键字信息(K1, K2, …, Kn)。关键字的个数 n 满足：Ceil(m/2)-1 <= n <= m-1 。Ki(i = 1, 2, …, n)为关键字，且关键字升序排序。Pi(i = 1, 2, …, n)为指向子树根节点的指针，P(i - 1)指向的子树的所有节点关键字均小于K(i)，但都大于K(i - 1)。所有叶子节点都在同一层，且不包含其它关键字信息。

注意：

m 阶指的是一个节点最多拥有 m 个孩子节点，而不是指的树的高度，即3阶 B-tree 是每个节点都最多拥有3个孩子节点。Ceil(m/2)为向上取整，例如 Ceil(3/2)=2，Ceil(5/2)=3

结合图来看，例如一棵3阶 B-tree 结构图。

如果各位客观要是觉得这个图不好看，那就换个简化版的图，这么贴心值不值得一个点赞呢。

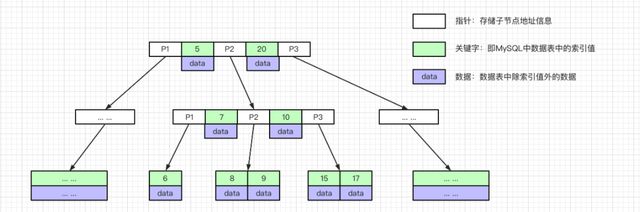
图中可以看到 B-tree 关键字(索引)和数据(除索引外的其他列数据)是放在一起的，没有存储冗余关键字(索引)，同时通过指针指向孩子节点，关键字左边的孩子节点都比关键字小，关键字右边的孩子节点都比关键字大。

B-tree 通过多路搜索的方式大大的降低了树的高度，大大减少了查找一个数据的磁盘 IO，比如我要查找6这个元素的信息，只需要3次磁盘 IO 就能找到想要的数据。

那么 MySQL 为什么没有选择 B-tree 而是使用了 B-tree 的变种 B+tree 嘞，跟着十一来看看 B+tree 的结构对比 B-tree 有啥区别再来回答这个问题。

#2. B+tree(B+树)

B+tree怎么定义呢？

B+树是B-树的变体，也是一种多路搜索树，其定义基本与 B-tree 相同，存在以下几点不同之处：

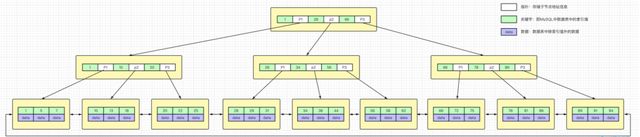
非叶子结点的子树指针与关键字个数相同非叶子节点只存储关键字信息(即非叶子节点只存储索引，不存储除索引外的其他字段信息)。所有叶子节点之间都有指针相连，指向下一个叶子结点。(当然MySQL做了优化，优化成了双向循环链表，啥是双向循环链表，看图就知道啦)数据记录都存放在叶子节点中。

一棵3阶 B+tree 如图。

简化版结构图片

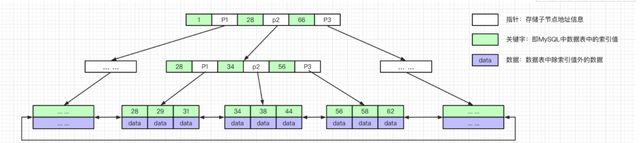
可以看到 B+tree 对比 B-tree 所有数据都存储在叶子节点中，非叶子结点只存储冗余索引，同时叶子结点之间使用双向循环链表链接。

 

那么又引出了下面两个问题，回答完这两个问题各位小伙伴就知道为什么 MySQL 选择 B+tree 不选择 B-tree 了。

为什么 B+tree 不在非叶子结点存储除索引外的其他数据呢？

答: 为了继续降低树的高度，同时让非叶子结点可以存储更多的索引。

详解：

在 MySQL 的 InnoDB 中，一个节点被称为一个数据页，这个数据页大小可以通过 show global status like 'Innodb_page_size'; 命令查询，默认是 16384b，也就是说一个数据页的大小是 16kb。

在 MySQL 的 InnoDB 中一个指针被定义为6字节，那么假设主键类型为 bigint (8字节)，叶子结点中一条数据为 1k (1024字节，通常一张二三十个字段的表一条记录大小都不会超过1k，除非是大数据类型)，那么一个高度为3的 B+tree 可以存储多少数据呢？

第一层存储索引数量：16384/(8+6) = 1170

第二层存储索引数量：16384/(8+6) = 1170

第三层叶子结点存储数据数量：16384/1024 = 16

也就是说一个3层高度的 B+tree 可以存储 1170*1170*16 = 21902400 条数据。

那么如果主键是 int 类型呢，就可以存储 1638*1638*16 = 42928704 条数据。

接下来对比一下 B-tree，同样以指针被定义为6字节，假设主键类型为 bigint，一条数据为 1k，3层高的 B-tree 可以存储多少条数据呢？

第一层存储数据数量：16384/(1024+6) = 15

第二层存储数据数量：16384/(1024+6) = 15

第三层存储数据数量：16384/(1024) = 16

也就是说一个3层高的 B-tree 可以存储 15*15*16 = 3600 条数据。

对比相同高度下的 B+tree 和 B-tree 可以存储数据的多少，这么巨大的差距，那当然选择 B+tree。

为什么叶子结点需要优化成双向循环链表？

答：因为 B+tree 所有的数据都在叶子结点中，叶子结点之间的双向循环链表是为了提高区间访问的性能，方便范围查找数据。

使用 B+tree 不使用 B-tree 原因总结：进一步降低树的高度 + 非叶子结点存放索引的数量 + 叶子结点间双向循环链表提高区间访问的性能，方便范围查找数据。

#四、Hash表

理解清楚了为什么 MySQL索引数据结构使用 B+tree 而不是 各种二叉树和 B-tree，那么为什么 99.99 的情况下都是 B+tree，而不使用 Hash 呢？

先来看看 Hash 作为索引有什么特点。

对索引的 key 进行一次 Hash 计算就可以定位出数据存储的位置。仅能满足 “=” 和 “IN”，不支持范围查询。hash冲突问题。

可以看到 Hash 仅能满足 “=” 和 “IN”，因为无序所以不支持范围查询，同时数据库大数据存储时容易产生 Hash 冲突，所以通常使用 B+tree。

#五、MyISAM索引实现

虽然 MyISAM 在 MySQL8.0 中已经废弃了，但是目前主流来说还是 MySQL5.7 的版本，所以还是说说 MyISAM 索引底层的数据结构。

首先需要 MySQL 安装的小伙伴们看这两篇：

• Linux(CentOS7)下二进制安装MySQL5.7.26(opens new window)
• Docker搭建MySQL并挂载数据(opens new window)

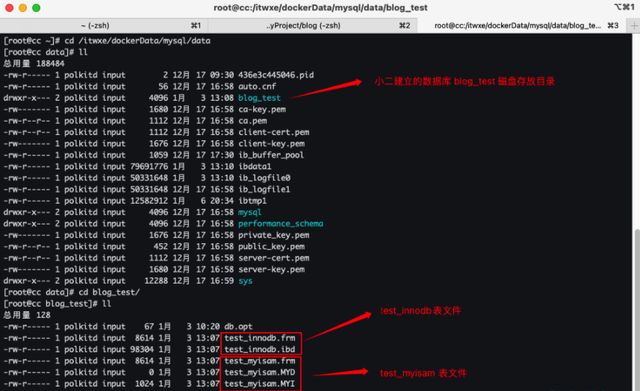
使用 docker 安装的方式，所以我的数据在
/itwxe/dockerData/mysql/data 目录下。

我创建了一个 blog_test 的数据库，在里面分表建了两张表 test_innodb 和 test_myisam。

CREATE TABLE `test_innodb` (
  `id` int(11) NOT NULL AUTO_INCREMENT,
  `name` varchar(255) NOT NULL,
  `age` int(11) NOT NULL,
  PRIMARY KEY (`id`)
) ENGINE=InnoDB DEFAULT CHARSET=utf8mb4;

CREATE TABLE `test_myisam` (
  `id` int(11) NOT NULL AUTO_INCREMENT,
  `name` varchar(255) NOT NULL,
  `age` int(11) NOT NULL,
  PRIMARY KEY (`id`)
) ENGINE=MyISAM DEFAULT CHARSET=utf8mb4;

来磁盘上面看看 MySQL 是怎么存放建立的库和表的。

InnoDB 存储引擎两个文件分别存储：

• frm：表结构文件
• ibd：表索引及数据文件

MyISAM 存储引擎三个文件分别存储：

• frm：表数据结构文件
• MYI：表索引文件
• MYD：表数据文件

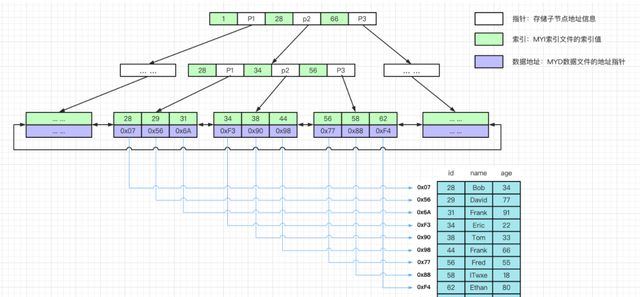
MyISAM 存储引擎把索引文件和数据文件分开来存放，结构如图。

MyISAM 存储引擎索引同样使用 B+tree，不过不同点在于没有将数据存储在叶子结点，叶子结点只存储了所有的索引 + 数据文件行记录的磁盘地址。

#六、InnoDB索引实现

前面已经看到了 InnoDB 的文件存储方式，与 MyISAM 不同的是，InnoDB 的索引和数据都放在叶子结点。

看完 InnoDB 存储引擎的索引实现，来思考一个公司中 DBA 关于主键规定的问题。

通常公司 DBA 建议 InnoDB 表必须建主键，并且推荐使用整型的自增主键，这是为什么呢？

• 为什么公司 DBA 建议 InnoDB 表必须建主键？表数据文件本身就是按照 B+tree 组织的一个索引结构文件，如果开发人员没有建立主键，MySQL 会选择唯一索引来作为主键索引构建索引数据文件，如果没有唯一索引会建立一个隐藏列来作为主键。那么能自己完成的事情当然自己完成，同时使用主键来查询单条记录时可以避免回表，啥是回表看到二级索引及联合索引实现就知道啦。
• 为什么推荐使用整型的自增主键？非整形主键下，例如 UUID，索引建立时比较大小问题（整形比较大小比UUID更快，UUID需要逐个字符转换为 ASCII 码逐个比较，虽然影响性能不大），同时非整形主键通常占用的空间更大，也就意味着一个索引页能够存放的索引数量不如整形主键。非整形主键下，每次插入主键的值近似于随机，因此每次新纪录都要被插到现有索引页得中间某个位置，那么 MySQL 不得不为了将新记录插到合适位置而移动数据，这增加了很多磁盘开销；而使用整形自增主键情况下，数据只需要一直往叶子结点后面放即可，大大减少索引页的分裂和移动数据产生的磁盘开销。

#七、二级索引及联合索引实现

可以看到上面的图都是以主键索引构建 B+tree，那么二级索引和联合索引是怎么实现 B+tree 嘞。

#1. 二级索引(辅助索引)

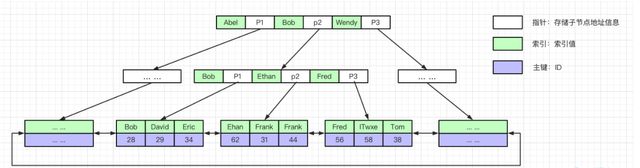
以 ALTER TABLE test_innodb ADD INDEX idx_name(name) USING BTREE; 为例，建立二级索引 B+tree。

二级索引在构建索引时叶子结点数据仅存放索引和主键 ID，并且以索引 name 字段来排序作为叶子节点关键字，那么例如要 SELECT * FROM test_innodb WHERE name = 'ITwxe'; ，那么会怎么查找呢？

首先，会通过二级索引 idx_name(name) 查询到 ITwxe，得到叶子结点主键 ID 为58后，会通过58去主键索引构建的 B+tree 中查询所有字段信息，这也就是所谓的 回表。

那么非主键索引结构叶子节点都存储完整的行记录不是查询更快吗更快？为什么 MySQL 非主键索引结构叶子节点存储的是主键值去回表查询，而不是存储所有行字段信息呢？

• 一致性问题，如果每个非主键索引叶子结点都存储完整行记录，那么当更新一条记录时，只有所有的索引中都更新成功这条记录才能说这条记录更新成功，增加了更新记录时的复杂性和事务的开销。
• 磁盘占用问题，如果每个非主键索引叶子结点都存储完整行记录，虽然速度会比回表查询更快，但是有多少个索引就会有多少份完整数据，那么原来占用1GB大小的表，如果有4个非主键索引，那么原来占用1GB大小的表就会占用5GB大小的磁盘，得不偿失。

#2. 联合索引(复合索引)

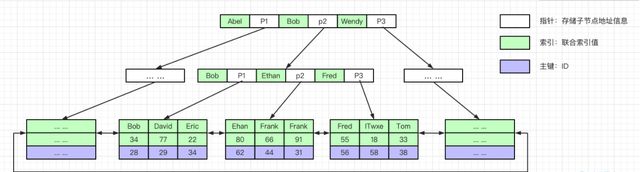
同理，以 ALTER TABLE test_innodb ADD INDEX idex_name_age(name, age) USING BTREE; 为例，建立联合索引 B+tree。

以看到，联合索引建立 B+tree 时，会以建立索引的顺序来排列数据，首先以 name 字段排序，再以 name 字段来排序。name 字段值如果相同，例如 Frank 那么就会以 age 来排列顺序，以此类推，最终同样查到相应的主键 ID 之后回表到以主键构建的 B+tree 中查询完整的行信息。

看完联合索引结构，想必各位小伙伴已经知道最佳左前缀原则是为什么第一个字段(name)一定要有才能生效了，因为只有第一个字段相同，第二个字段(age)才是有顺序排列的。

同时如果同时存在两个索引 idx_name(name) 和 idex_name_age(name, age) ，那么 idx_name(name) 即为冗余索引，在建立索引时只需要建立联合索引 idex_name_age(name, age)，想必各位小伙伴聪明的小脑袋对比一下两个结构图就知道啦~

#3. 聚簇索引和稀疏索引

聚簇索引即叶子结点中包含所有完整行记录，叶子节点中包含索引及其他所有字段信息，InnoDB 存储引擎中以主键索引构建的 B+tree 即为聚簇索引，其他的皆为稀疏索引。例如二级索引、联合索引、MyISAM存储引擎的索引全是稀疏索引。

 感谢大家阅读，本人见识有限，写的博客难免有错误或者疏忽的地方，还望各位大佬指点，在此表示感激不尽。文章持续更新中…....