【树】从二叉树到空间索引树

1 二叉树系列

这里主要介绍满二叉树、完全二叉树、二叉搜索树、平衡二叉树、红黑树等。首先通过形象图来记录一下这几种二叉树之间的图形关系，随后再谈谈这些树的注意事项。

1.1 二叉树

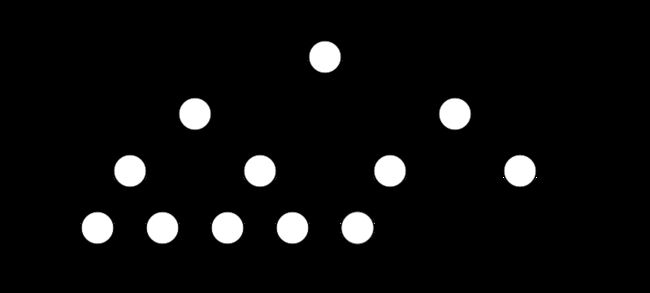
满二叉树

满二叉树是一个每层的结点数都达到最大值的二叉树，其定义和树型结构如下：

如果一个二叉树的层数为 $k$，且结点总数是 $2^k-1$ ，则它就是满二叉树。

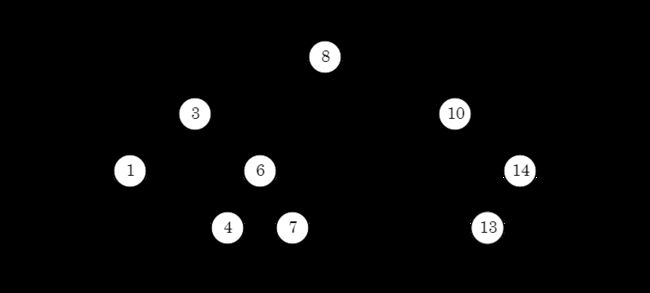
完全二叉树

完全二叉树由满二叉树转化而来，也就是将满二叉树从最后一个节点开始删除，一个一个从后往前删除，剩下的就是完全二叉树。如下图所示：

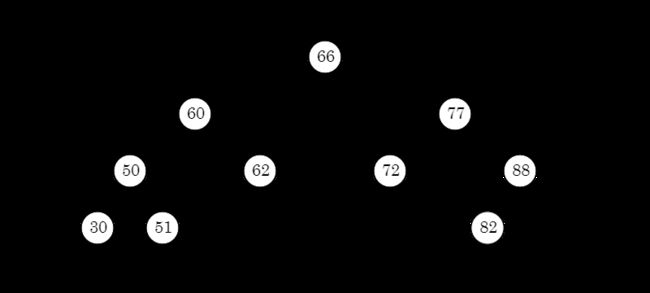
二叉搜索树

二叉搜索树是一颗左子树都比其根节点小，右子树都比根节点大的树。如下图所示：

二叉搜索树具有如下性质：

a. 若左子树不空，则左子树上所有节点的值均小于其根节点的值；
b. 若右子树不空，则右子树上所有节点的值均大于或等于其根节点的值；
c. 左、右子树也分别为二叉搜索树。

平衡二叉树

平衡二叉树由前苏联的数学家 Adelse-Velskil 和 Landis 在 1962 年提出，根据科学家的英文名也称为 AVL 树。它的提出主要是为了保证树不至于出现二叉查找树的极端一条腿长现象，尽量保证两条腿平衡。因此其定义如下：

平衡二叉树要么是一棵空树，要么保证左右子树的高度之差不大于 1，并且子树也必须是一棵平衡二叉树。

平衡二叉树不一定是完全二叉树，如上图所示。需要注意的是，平衡二叉树的全称是平衡二叉搜索树，所以其本质上还是个二叉搜索树，搜索效率很高，但是其在添加和删除时需要进行复杂的旋转以保持整个树的平衡。

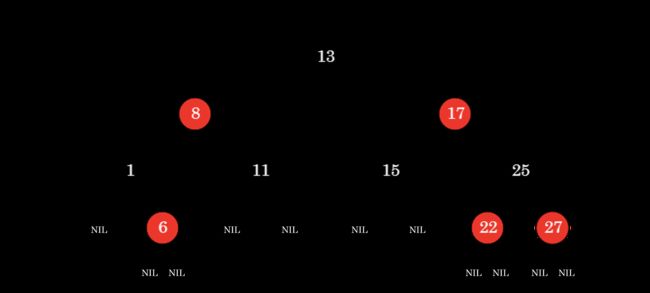
红黑树

红黑树起源于 Rudolf Bayer 1972 年发明的平衡二叉 B 树（Symmetric Binary B-trees），并于 1978 年由 Leo J. Guibas 和 Robert Sedgewick 修改为如今的红黑树。红黑树的本质其实是对概念模型 2-3-4 树 的一种实现， 2-3-4 树是一颗阶数为 4 的 B 树，有关这一概念我们在后文的 B 系列树中进行展开，这里先简单了解一下这个概念。

红黑树的性质及定义如下：

a. 每个节点要么是黑色，要么是红色；
b. 根节点是黑的；
c. 每个叶节点（NIL）是黑的；
d. 每个红色节点的两个子节点一定都是黑的；
e. 任意一节点到每个叶子节点的路径都包含数量相同的黑节点。

从性质和操作上来看，红黑树是平衡二叉树的升级版，具有更高的性能：

a. AVL 的左右子树高度差不能超过 1，每次进行插入/删除操作时，几乎都需要通过旋转操作保持平衡；
b. 在频繁进行插入/删除的场景中，频繁的旋转操作使得 AVL 的性能大打折扣；
c. 红黑树通过牺牲严格的平衡，换取插入/删除时少量的旋转操作，整体性能优于 AVL；
红黑树插入时的不平衡，不超过两次旋转就可以解决；
删除时的不平衡，不超过三次旋转就能解决；
d. 红黑树的红黑规则，保证最坏的情况下，也能在 $O({\log }_{2}n)$ 时间内完成查找操作。

1.2 平衡二叉树

计算机科学中，AVL 树是最早被发明的自平衡二叉查找树。AVL 树任一节点对应子树的最大高度差为 1，因此它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下的时间复杂度都是 $O(\log n)$。

• 平衡二叉树的定义

  性质 1. 可以是空树；
  性质 2. 假如不是空树，任何一个节点的左子树和右子树都是平衡二叉树，并且高度之差的绝对值不超过 1。

平衡二叉树实现的关键变量是树的深度 depth，即在树的每个节点中添加深度信息，并据此计算平衡因子：

Balance Factor：某节点的左子树与右子树的高度差即为该节点的平衡因子，值域 $\{-1,0,1\}$。

一颗 C++ 平衡二叉树的定义代码如下所示：

typedef struct AVLNode* Tree;
struct AVLNode{
    int   depth;  // 当前节点的高度
    Tree  parent; // 父节点
    int   value;  // 节点值
    Tree  lchild; // 左节点
    Tree  rchild; // 右节点
    
    AVLNode(int val = 0){
        parent = NULL;
        depth = 0;
        lchild = rchild = NULL;
        this->val = val;
    }
    void rotation(); // 旋转操作
}

左旋和右旋

当节点平衡因子小于 0 时，需要执行树的左旋操作。其操作流程为：1^st 右节点变成该节点；2^nd 右节点的左子树变成该节点右子树；3^rd 该节点变成右节点的左子树。

同理，可将右旋操作的流程描述为：1^st 左节点变成该节点；2^nd 左节点的右子树变成该节点左子树；3^rd 该节点变成左节点的右子树。

插入失衡

假设一颗 AVL 树的某个节点为 A，有四种操作会使 A 的左右子树高度差大于 1而破坏原有平衡性，即：

插入方式	描述	旋转方式
LL	在 A 的左子树根节点的左子树上插入节点而破坏平衡	右旋转
RR	在 A 的右子树根节点的右子树上插入节点而破坏平衡	左旋转
LR	在 A 的左子树根节点的右子树上插入节点而破坏平衡	左子左旋后 A 右旋
RL	在 A 的右子树根节点的左子树上插入节点而破坏平衡	右子右旋后 A 左旋

删除失衡

二叉搜索树的删除分为四种情况：① 删除叶子节点 、② 删除的节点只有左子树、③ 删除的节点只有右子树以及 ④ 删除的节点既有左子树又有右子树。二叉搜索树的删除中 ①②③ 操作较为便捷，只需将父节点链接到不为空的节点上即可；操作 ④ 思路上需要一点数学思想，即：

情况 ④ 的删除 可以记录待删除结点左子树当中值最大的结点或是待删除结点右子树当中值最小的结点的值 $V$ 并将该节点删除，随后将待删除结点的值改为 $V$ 即可维护二叉搜索树的结构。

AVL 树和二叉搜索树的删除操作情况一致，都分为四种情况；不过 AVL 树在删除节点后需要重新检查平衡性并修正树结构。需要注意的是，插入操作只需对插入栈中的弹出的第一个非平衡节点进行修正，而删除操作需要修正栈中所有的非平衡节点。

• 删除操作步骤

  1^st 以 ①②③ 为基础尝试删除节点，并将访问节点入栈；
  2^nd 删除成功则依次检查栈顶节点的平衡状态，遇到非平衡节点即进行旋转平衡，直到栈空；
  3^rd 删除失败则为 ④，找到被删除节点的右子树最小节点并删除它，将访问节点继续入栈；
  4^th 依次检查栈顶节点的平衡状态和修正直到栈空。

对于删除操作造成的非平衡状态的修正，可以这样理解：左子树上删除节点其实就相当于在右子树上插入节点，反之右子树上删除节点其实就相当于在左子树上插入节点。也就是说，失衡时，更高的子树相当于在原有平衡状态下插入了一个节点，所以需要做相应的旋转操作。

1.3 红黑树

红黑树并不是一个完美平衡二叉查找树，其维持的是一种黑色完美自平衡，它可以在 $O(\log n)$时间内做查找、插入和删除。红黑树的定义如下：

• 红黑树的定义

  性质 1. 每个节点要么是黑色，要么是红色；
  性质 2. 根节点是黑的；
  性质 3. 每个叶节点（NIL）是黑的；
  性质 4. 每个红色节点的两个子节点一定都是黑的；
  性质 5. 任意一节点到每个叶子节点的路径都包含数量相同的黑节点。

一颗 C++ 红黑树的定义代码如下所示：

typedef RBNode* Tree;
enum Colour { RED, BLACK };
struct RBNode{
    Tree parent;
    Tree left;
    Tree right;
    int color;
    int value;
    
    void recolor(); // 重新着色
    void rotation();// 旋转操作
}

算法公式

插入节点时会先尝试 recolor，如果 recolor 不能达到红黑树的要求则尝试 rotation；实红黑树的关键玩法就是弄清楚 recolor 和 rotation 的规则，具体的算法公式如下：

1. 将新插入的节点 X 标记为红色；
2. 如果 X 是根节点 `root` 则标记为黑色；
3. 如果 X 的 `parent` 是黑色，则直接插入即可；
4. 如果 X 的 `parent` 不是黑色，且 X 也不是 `root`，则分两种情况：
   4.1. 如果 X 的叔父节点 `uncle` 是红色：
        4.1.1 将 `parent` 和 `uncle` 标记为黑色；
        4.1.2 将 `grand parent` 祖父节点标记为红色；
        4.1.3 让 X 节点的颜色与 X 的祖父的颜色相同，然后重复 2、3 步骤；
   4.2. 如果 X 的叔父节点是黑色，则分四种情况：
        4.2.1 左左，即 `P` 是 `G` 的左孩子，`X` 是 `P` 的左孩子；
        4.2.2 左右，即 `P` 是 `G` 的左孩子，`X` 是 `P` 的右孩子；
        4.2.3 右左，为 3.2.2 的镜像；
        4.2.4 右右，为 3.2.1 的镜像；

如上所示，4.2 的四种情况对应平衡二叉树插入失衡的四种树的旋转操作；执行完树的旋转操作之后，树就自然而然的实现平衡了。

2 B 树系列

B 树全名 Balance Tree，译作平衡多路查找树，由 R.Bayer 和 E.mccreight 于 1970 年提出，这种树型结构主要用来做查找。前文提到的 AVL 树 和红黑树，都假设所有的数据放在主存当中，但当数据量达到了亿级别，主存当中根本存储不下时，就需要考虑以块的形式从磁盘读取数据；与主存的访问时间相比，磁盘的 I/O 操作相当耗时，针对这一问题所提出的 B 树其主要目的就是减少磁盘的 I/O 操作。最直观反应磁盘数据读取操作次数的就是树的高度，在平衡系列树中，一般树的高度为 $\log n$，而 B 树基于其本身节点所包含的键的定义可以对树的高度进行定制化处理，其节点键的个数与磁盘块的个数一样。

度：一个结点含有的子结点的个数称为该结点的度；
阶：一棵树的最大孩子数。

2.1 B 树

B 树中所有结点中孩子结点个数的最大值称为 B 树的阶，通常用 $m$ 表示，从查找效率考虑，一般要求 $m⩾3$。一棵 $m$ 阶 B 树或者是一棵空树，或者是满足以下条件的 $m$ 叉树：

• B 树的定义

  性质 1. 根节点至少有 2 个子节点；
  性质 2. 每个非根节点的关键字个数 $j$ 满足 $\lceil m/2\rceil ⩽j⩽m-1$；
  性质 3. 每个结点中的关键字都按照从小到大的顺序排列，左子树小于它，右子树大于它；
  性质 4. 所有叶节点都位于同一层。

同时，B 树也可以通过最小度，即当前节点最小孩子个数 $t$ 来定义。若采用这种方式定义 B 树，则上述定义中的性质 2 需要修改为：

​ 性质 2. 每个非根节点的关键字个数 $j$ 满足 $t-1⩽j⩽2t-1$；

一颗 C++ B 树的定义代码如下所示：

typedef BTreeNode* Tree;
struct BTreeNode{
    int* keys;           // 关键字数组
    Tree** children;     // 孩子节点指针数组
    int t;               // 最小度，用于定义节点关键字个数的阈值
    int n;               // 当前节点关键字个数
    
    void traverse();     // 中序遍历
    Tree* search(int k); // 从树中查找关键字 k 
}

B 树的关键点在于节点的查找、插入和删除，在进行插入时，若待插节点的关键字个数超出其容纳阈值，就需要以插入关键字后的关键字列表中间 key 为中心分裂为左右两部分，然后将该 key 插入到父节点中，将分裂后的左部分作为该 key 的左节点，分裂后的右部分作为该 key 的右节点。

插入算法

1. 初始化插入节点 $x$ 为根节点；
2. 当 $x$ 不是叶子节点时执行如下操作：
   2.1. 找到 $x$ 的下一个要被访问的孩子节点 $y$；
   2.2. 若 $y$ 没有满，则将该节点 $y$ 作为新的 $x$；
   2.3. 若 $x$ 已满，则拆分 $y$，节点 $x$ 的指针指向节点 $y$ 的两部分：
        若 key 比 $y$ 中间的关键字小，则将 $y$ 的第一部分作为新的 $x$;
        否则，将 $y$ 的第二部分作为新的 $x$；
        拆分后，将 $y$ 中的一个关键字移动到它的父节点 $x$ 中。

删除算法

1. 待删除的关键字 $k$ 在结点 $x$ 中，且 $x$ 是叶子结点，删除关键字 $k$；

2. 待删除的关键字 $k$ 在结点 $x$ 中，且 $x$ 是内部结点，分以下三种情况：

   2.1. 如果位于结点 $x$ 中的关键字 $k$ 之前的第一个孩子结点 $y$ 至少有 $t$ 个关键字，则在孩子结点 $y$ 中找到 $k$ 的前驱结点 $k_0$ ，递归地删除关键字 $k_0$，并将结点 $x$ 中的关键字 $k$ 替换为 $k_0$.

   2.2. 如果 $y$ 所包含的关键字少于 $t$ 个关键字，则检查结点 $x$ 中关键字 $k$ 的后一个孩子结点 $z$ 包含的关键字的个数，如果 $z$ 包含的关键字的个数至少为 $t$ 个，则在 $z$ 中找到关键字 $k$ 的直接后继 $k_1$ 然后删除 $k_1$ ，并将关键 $k$ 替换为 $k_1$ .

   2.3. 如果 $y$ 和 $z$ 都只包含 $t-1$ 个关键字，合并关键字 $k$ 和所有 $z$ 中的关键字到结点 $y$ 中，结点 $x$ 将失去关键字 $k$ 和孩子结点 $z,y$ 此时包含 $2t-1$ 个关键字，释放结点 $z$ 的空间并递归地从结点 $y$ 中删除关键字 $k$ .

3. 如果关键字 $k$ 不在当前在内部结点 $x$ 中，则确定必包含 $k$ 的子树的根结点 $x.c(i)$ ，这里需要确认 $k$ 确实在 B 树中。如果 $x.c(i)$ 只有 $t-1$ 个关键字，必须执行下面两种情况进行处理：

   3.1. 如果 $x.c(i)$ 及 $x.c(i)$ 的所有相邻兄弟都只包含 $t-1$ 个关键字，则将 $x.c(i)$ 与 一个兄弟合并，即将 $x$ 的一个关键字移动至新合并的结点，使之成为该结点的中间关键字，将合并后的结点作为新的 $x$ 结点 .

   3.2. $x.c(i)$ 仅包含 $t-1$ 个关键字且 $x.c(i)$ 的一个兄弟结点包含至少 $t$ 个关键字，则将 $x$ 的某一个关键字下移到 $x.c(i)$ 中，将 $x.c(i)$ 的相邻的左兄弟或右兄弟结点中的一个关键字上移到 $x$ 当中，将该兄弟结点中相应的孩子指针移到 $x.c(i)$ 中，使得 $x.c(i)$ 增加一个额外的关键字。

2.2 B+ 树

B+ 树是应文件系统所需而出的一种 B 树的变型树，其也是一种多路搜索树。为叶子结点增加链表指针，所有关键字都在叶子结点中出现，非叶子结点作为叶子结点的索引，B+ 树总是到叶子结点才命中。B+ 树的优点：

1. 方便扫库，B 树必须用中序遍历的方法按序扫库，而 B+ 树直接从叶子结点挨个扫一遍就完了。
2. B+ 树支持 range-query 区间查询，非常方便，而B树不支持；这是数据库选用 B+ 树的最主要原因。

• B+ 树与 B 树定义的区别是：

  区别 1. 有 $n$ 棵子树的结点中有 $n$ 个关键字，关键字不存数据只用来索引，所有数据均保存在叶子节点；
  区别 2. 叶子结点包含全部关键字及指向记录的指针，叶子节点本身依关键字大小顺序链接；
  区别 3. 非终结点为索引部分，仅包含其子树的最大或最小关键字；

通常在 B+ 树上有两个头指针，一个指向根结点，一个指向关键字最小的叶子结点。

2.3 B* 树

B* 树是 B+ 树的变体，在 B+ 树的非根和非叶子结点再增加指向兄弟的指针。将结点的最低利用率从1/2 提高到2/3；B* 树的优点：

B* 树分配新结点的概率比 B+ 树要低，空间使用率更高。

B+ 树的分裂：当一个结点满时，分配一个新的结点，并将原结点中 1/2 的数据复制到新结点，最后在父结点中增加新结点的指针；B+ 树的分裂只影响原结点和父结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针；
B 树的分裂*：当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制 1/3 的数据到新结点，最后在父结点增加新结点的指针。

3 空间索引系列树

3.1 KD 树

KD, K-Dimension-Tree，即多维二叉树，是空间二叉树的一种特殊情况；KD 树中储存着 K 维的点的信息，是对 K 维空间进行划分的一种数据结构；一般用来解决二维空间和三维空间的信息检索。

3.2 四叉树与八叉树

四叉树

四叉树，又称四元树，是一种每一个节点上有四个子区块的树状数据结构，常用于二维空间数据的分析分类；四叉树由 Raphael Finkel 与 J. L. Bentley 于 1974 年提出，其四个子区块范围可以是方形或矩形或其他任意形状。

八叉树

Octree，八叉树，是一种用于描述三维空间的树状数据结构，其每个节点表示一个正方体的体积元素，每个节点有八个子节点，这八个子节点所表示的体积元素加在一起就等于父节点的体积。一般中心点作为节点的分叉中心。

3.2 R 树与 RD 树

R 树作为 B 树向多维空间发展的另一种形式，是一种用于高效地进行多维空间范围查询的空间数据结构。它特别适用于最近邻搜索和窗口查询。R 树是一种平衡树结构，其中每个节点表示空间中的一个超矩形。根节点表示整个空间，每个子节点表示空间的一个子区域。树是通过沿着选择的轴将空间分成两半，然后递归地将每半分割，直到满足停止条件而构建的。

当使用对象变成文档时，就无法直接使用 R 树了，因为无法为文档定义一个矩形框。但我们可以把这种方法在集合类型上稍作改动，称作 RD 树（RD是 Russian Doll 的意思）；RD 树的思想就是用集合替代矩形框，也就是说一个集合可以包含其它子集。

在这里插入代码片

4 其他树

线段树

线段树又称区间树，是一种基于分治思想的二叉树结构，每个节点代表一段区间，和按照利用二进制性质划分区间的树状数组相比，线段树是一种更加通用的数据结构。线段树的每个节点代表一个区间，叶子节点代表输入序列中的单个元素，非叶子节点代表输入序列中的一些元素的区间。

线段树的主要应用是解决区间查询问题，例如区间最小值、区间最大值、区间和等问题。线段树可以在 $O(\log n)$ 的时间内应答这些查询。在下面的示例代码中，我们定义了一个 SegmentTreeNode 结构体，表示线段树的节点。在 build 函数中，我们递归地构建线段树。在 query 函数中，我们递归地查询区间和。

#include 
#include 

using namespace std;

// 线段树节点
struct SegmentTreeNode {
    int start, end;
    int sum;
    SegmentTreeNode *left, *right;

    SegmentTreeNode(int start, int end) {
        this->start = start;
        this->end = end;
        this->sum = 0;
        this->left = nullptr;
        this->right = nullptr;
    }
};

// 构建线段树
SegmentTreeNode* build(vector<int>& nums, int start, int end) {
    if (start > end) {
        return nullptr;
    }

    SegmentTreeNode* root = new SegmentTreeNode(start, end);

    if (start == end) {
        root->sum = nums[start];
    } else {
        int mid = start + (end - start) / 2;
        root->left = build(nums, start, mid);
        root->right = build(nums, mid + 1, end);
        root->sum = root->left->sum + root->right->sum;
    }

    return root;
}

// 区间查询
int query(SegmentTreeNode* root, int start, int end) {
    if (root == nullptr) {
        return 0;
    }

    if (root->start == start && root->end == end) {
        return root->sum;
    }

    int mid = root->start + (root->end - root->start) / 2;
    if (end <= mid) {
        return query(root->left, start, end);
    } else if (start > mid) {
        return query(root->right, start, end);
    } else {
        return query(root->left, start, mid) + query(root->right, mid + 1, end);
    }
}

int main() {
    vector<int> nums = {1, 3, 5, 7, 9, 11};
    SegmentTreeNode* root = build(nums, 0, nums.size() - 1);

    cout << query(root, 0, 2) << endl; // 输出9
    cout << query(root, 2, 5) << endl; // 输出32

    return 0;
}