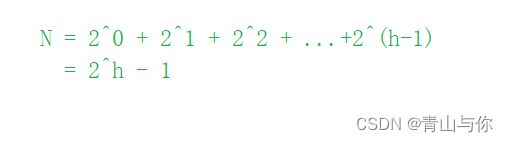树与二叉树的存储与遍历

---

一、树概念

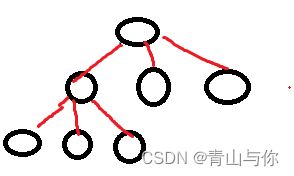
如前面的顺序表，链表，栈和队列都是线性的数据结构，树是非线性的结构。树可以有n个结点，n>=0,当n=0是就表示树为空
n>0,代表树不为空，不为空的树，它只有一个根结点，然后其余的结点又是构成互不相交的树，然后这些树本身又是一棵树，这些树且为根节点的子树。
任何一棵树都由两部分构成
1、根
2、子树
然后子树又由根和子树构成…无穷无尽的，直到为空为止，所以树又是递归定义的

根是唯一的但是它的子树有许多，莫得限制，且这些子树它们永远也不会相交。
树节点
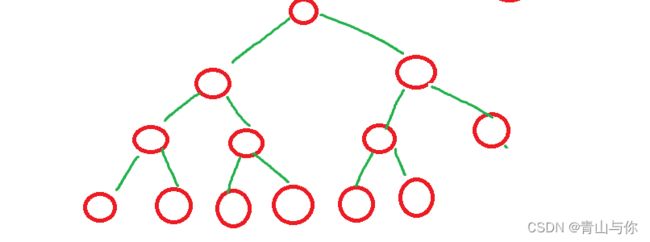
树是由许多结点构成的，那么每个结点又是啥样的嘞？树的每个结点它有可能会有子树，且它拥有子树的数量也是它该节点的度，那么整棵树的度为多大？，一颗树的度为该树内部结点的度的最大值

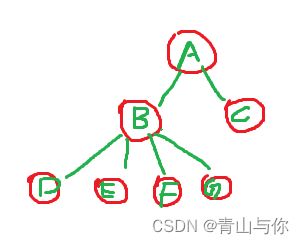
上述这颗树的度也是结点B的度，为4，然后就像D,E,F,G,C，这些结点它后面没有子树了，也就是度为0的结点，这些结点也有另一个名字：叶子结点，然后嘞像B结点为非叶子结点。

节点关系
然后这些结点之间有什么关系？
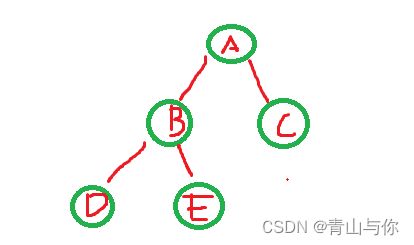
这些结点它的子树的根也叫做它的孩子，然后这个结点也是它孩子结点的双亲

如结点A

蓝颜色圈起来的为它的子树，然后这些子树的根B,C又为A结点的孩子，然后嘞A也是它两个孩子结点的双亲结点，如A结点是B和C结点的双亲，B,C结点为A的孩子那么B,C它们两个结点之间又是什么关系？它们有同一个双亲，那么有同一个双亲在我们现实生活中难道不是兄弟吗，没错在树中有同一个双亲结点的孩子结点它们之间互为兄弟关系，称为兄弟结点。其实这些关系是借鉴生活中对应的家庭中的关系

树高度
树的高度也叫树的层次，树的根结点所在为第一层，然后它的孩子为第二层

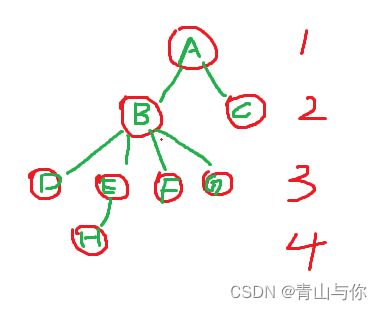
这颗树高度为4，如果给定某个结点在第h层，那么它的孩子结点在第h+1层

树的存储
由于每个节点的孩子可以有很多个，根本不知道它的孩子节点有多少个，除非树中已经明确给出了树的度为n，那么就可以定义n个孩子节点
但是如果不知道度为多少，应该如何定义树？
有一种存储方式很适合树结构表示：左孩子又兄弟表示法

typedef int TDataType;
typedef struct BTNode
{
	struct BTNode* leftchild;//指向根节点的左孩子
	struct BTNode* rightbrother;//指向左孩子它的右兄弟
	TDataType data;
}BTNode;

这种方法好处是不管该节点有多少孩子节点，都只需要知道它的左孩子然后就可以找到它其他的孩子节点，不论怎样都只有两个指针

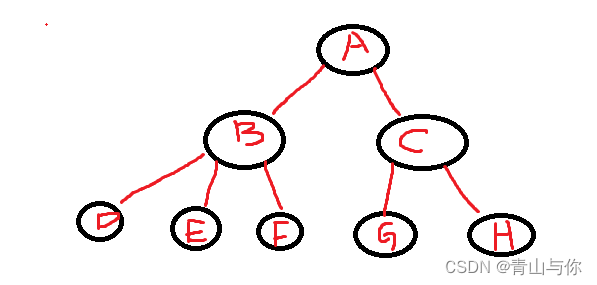
A的右兄弟为空然后A有两个孩子，但是他不会管他自己有多少孩子节点，它只需要找到它的左孩子，然后再通过它的左孩子就可以找到它的右孩子了。

通过每一颗子树的根找到它的左孩子，然后再找左孩子的右兄弟，这个只有两个指针，感觉上像是二叉树，但是并不是，二叉树一个节点最多只有两个孩子，但是这里一个节点可以有多个孩子节点
不管有多少个孩子都只需要找第一个孩子，然后剩下的用兄弟指针去链接，每个节点都是两个指针，这点有些像二叉树，那么下面就引入二叉树

二、二叉树

二叉树就是树的度不大于2，也就是每个结点它的孩子结点不超过两个，每个结点的子树不超过两棵，然后在左边的那个结点为左孩子，右边的结点为右孩子。每一棵二叉树由根，左子树，右子树构成。二叉树也具有树的基本特性

左边的为左子树，右边的为右子树 二叉树可以为空，也可以只有一个节点（根），亦可以只有左子树或者只有右子树，还可以左子树和右子树都有

但是二叉树中有两个特殊的树

二叉树又有几种特殊的

• 满二叉树
• 完全二叉树

满二叉树叶子结点在同一层上且叶子结点只出现在最后一层，非叶子结点的度一定为2，就是每一层都是满的，那么高度为h的满二叉树有多少的节点？

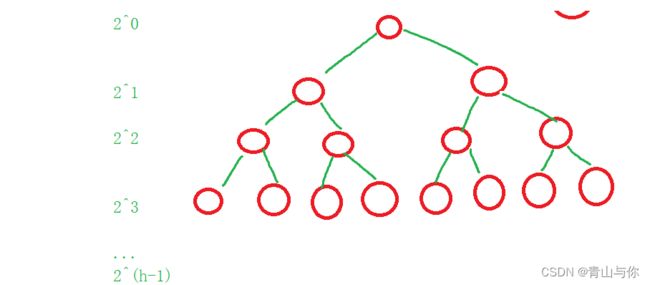
每一层节点个数相加可以发现是一个等比数列，节点个数也就是等比数列求和为 2^h - 1

那么假设满二叉树有N个节点，求其高度h

由于log₂^(N-1)算出的结果很大程度上可能是小数，但是高度一般用整数表示，那么以得到的值向下取整得到整数然后再加一就为满二叉树的高度

还有就是同普通二叉树相比满二叉树的结点个数是最多的.

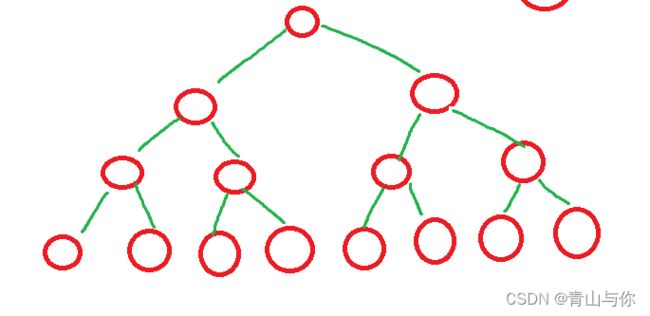
完全二叉树

如果二叉树有h层，那么它的前h-1层都是满的，最后一层不一定满但是要求最后一层从左到右是连续的

那么假设完全二叉树高度为h的节点数量的范围是多少？

N ~[log^(h-1)^,log^h^-1] 最少前h-1层是满的第h层只有一个节点，最多也就是一棵满二叉树

任意一棵二叉树
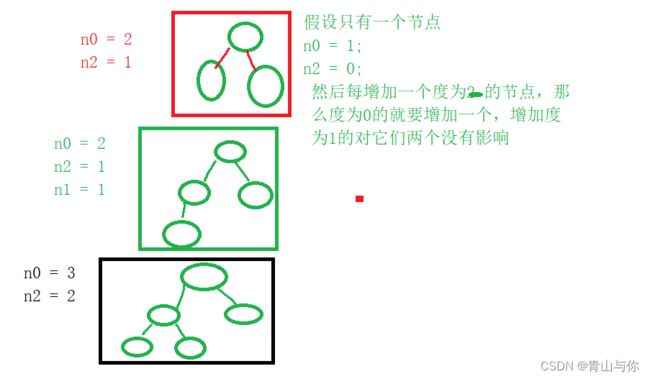
它的叶子结点数一定比度为2的结点数目多一个，即假设叶子结点数为n₀,度为2的结点数为n₂,那么n₀=n₂+1;

且完全二叉树中度为1的节点最多只有一个，或者就是没有度为1的节点，因为其是连续的，最多只会缺少右孩子

三、二叉树的存储与遍历

二叉树的存储
二叉树用数组存储容易会造成空间上的浪费，如果二叉树只有左子树或者右子树

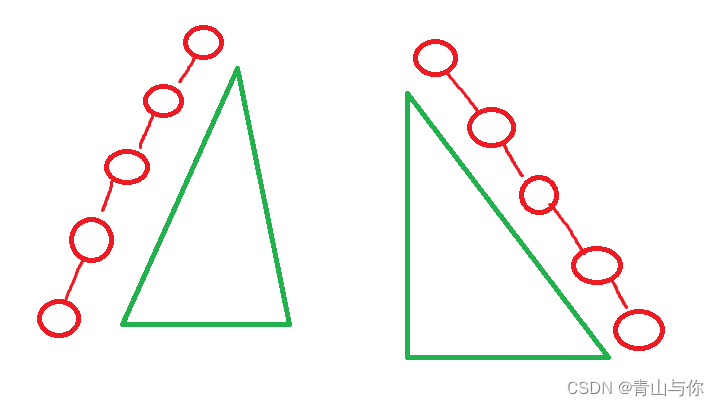
绿色部分那片内存空间浪费了，没有被使用，因此用链式存储结构较为合适
但是如果是一棵完全二叉树的话，用顺序存储结构就较好了，因为完全二叉树是连续的

二叉树链式存储结构

typedef int TDataType;
typedef struct BTNode
{
	struct BTNode* left;
	struct BTNode* right;
	TDataType data;
}BTNode;

一个指针指向它的左孩子，一个指针指向右孩子

二叉树遍历
二叉树遍历方式主要有四种，但是我这里先分享三种遍历方式

• 前序遍历
• 中序遍历
• 后序遍历

先手动构建二叉树的节点

BTree* BuyNode(TDataType x)
{
	BTree* newnode = (BTree*)malloc(sizeof(BTree));
	if (newnode == NULL)
	{
		perror("malloc fail\n");
		return NULL;
	}
	newnode->data = x;
	newnode->left = NULL;
	newnode->right = NULL;
	return newnode;
}

然后再自己创建一棵二叉树叭

BTree* BTCreat()
{
	BTree* newnode1 = BuyNode(1);
	BTree* newnode2 = BuyNode(2);
	BTree* newnode3 = BuyNode(3);
	BTree* newnode4 = BuyNode(4);
	BTree* newnode5 = BuyNode(5);
	BTree* newnode6 = BuyNode(6);
	newnode1->left = newnode2;
	newnode1->right = newnode3;

	newnode2->left = newnode4;
	newnode2->right = NULL;

	newnode3->left = newnode5;
	newnode3->right = newnode6;

	newnode5->left = NULL;
	newnode5->right = NULL;
	newnode6->left = NULL;
	newnode6->right = NULL;
	return newnode1;
}

前序遍历
前序遍历究竟是如何遍历二叉树的呢？
由于一棵二叉树由三部分构成：根、左子树、右子树

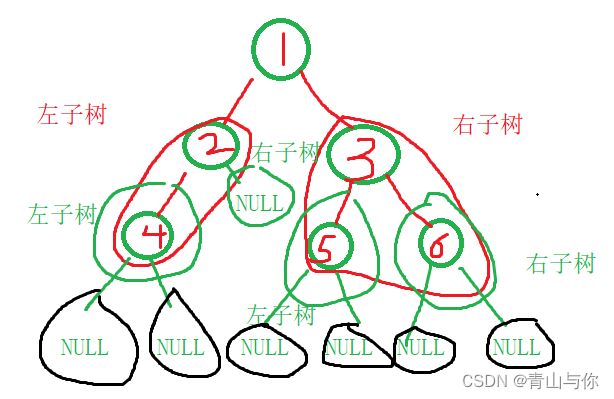
每一棵子树可以拆分为三部分，一直拆，直到子树为空就不可再拆分了

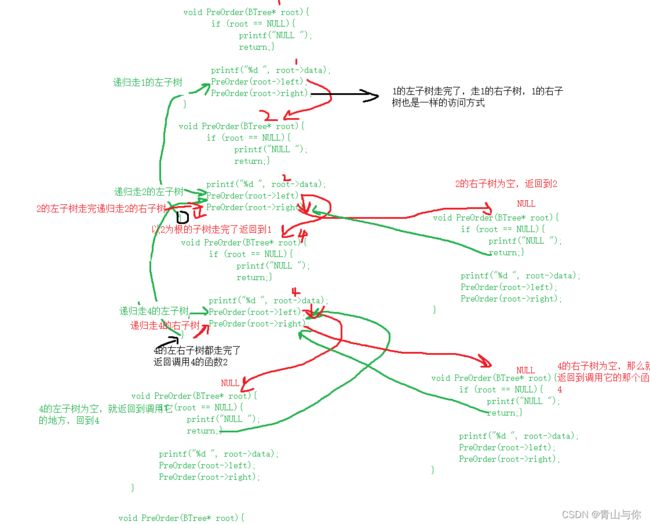
如果一棵二叉树是空，那么直接返回空，否则就是先访问这棵二叉树的根节点，然后再前序遍历它的左子树，它的左子树又是先访问它的根，然后又是左子树，当它的左子树以前序遍历访问直到空之后再以同样的前序遍历访问它的右子树，而它的右子树又是先遍历它的左子树依此直到为空，可以观察到访问是递归的，

前序遍历就是先访问其根，然后递归访问它的左子树，而左子树又由根，左子树，右子树，每一棵子树都由根，左子树，右子树构成，以前序遍历访问下去直到访问到空则返回然后访问它的右子树，右子树为空再返回，回溯了访问它双亲结点的右子树，最后回溯到整棵树的根，然后开始遍历访问整棵树的右子树，访问它的右子树时同样遵循先访问根，再访问左子树，最后访问右子树，遇到空则开始返回回溯

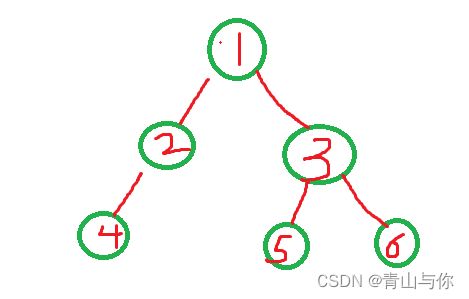
先访问 1，然后走它的左子树2，而它的左子树2又有根，左子树，右子树，访问2，然后再走它的左子树4，访问4，然后走4的左子树，4的左子树为空，代表4的左子树走完了，那么走它的右子树，它的右子树也为空，那么以4为子树作为2的左子树走完了，这回开始走2的右子树，2的右子树为空，那么就代表以2为子树作为1的左子树走完了，这回开始走1的右子树。
而1的右子树3不为空，又开始先访问3，然后走3的左子树5，访问5，然后走5的左子树，5的左子树走完了就代表以5为子树作为3的左子树走完了开始走3为子树它的右子树6不为空，访问6再走它的左子树，右子树最后就是全部都访问完了

这里前序我是将其空都算上的便于理解
前序 1 2 4 NULL NULL NULL 3 5 NULL NULL 6 NULL NULL
每一棵树都是由根，左子树，右子树构成

void PreOrder(BTree* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	printf("%d ", root->data);
	PreOrder(root->left);
	PreOrder(root->right);
}

前序遍历递归展开图

右子树也是一样的展开

中序和后序遍历的展开图这里就不再画了

中序遍历先访问左子树、再根、最后右子树

//中序遍历先访问每颗子树的左子树，直到左子树为空，才返回然后访问根，然后再访问以这个根为子树的右子树，右子树又访问其左子树，
//若干个子问题，一直拆，每棵树又由根，右子树，左子树三部分构成
//在中序遍历时要先访问每颗子树的左子树，直到以它为根的左子树为空，才访问它然后再访问其右子树

//每访问一次子树都是一次函数调用，且每一次函数调用都开辟一个函数栈帧用来维护这次函数栈帧开辟的空间，且每次返回时函数栈帧弹出，函数栈帧跳到调用它的
//那个函数以维护它的栈帧空间，且函数调用使用空间是允许重复的，即一次函数调用返回之后这块空间回收给操作系统然后下一次再调用其他函数
//又可以用这块内存空间
void InOrder(BTree* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}

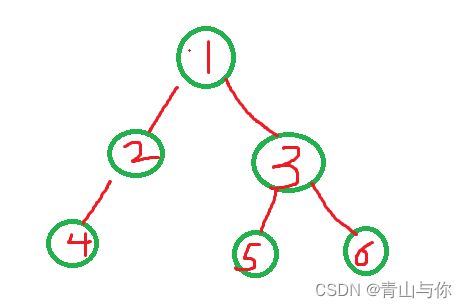
中序 NULL 4 NULL 2 NULL 1 NULL 5 NULL 3 NULL 6 NULL

后序遍历先访问左子树、再右子树，最后访问根

//先访问根的左子树，然后再访问右子树最后访问根
// 左子树又拆分为根左子树右子树然后又先访问左子树，后右子树最后根
// 直到那颗子树左右子树都为空然后就访问它（根），然后回溯到它的双亲结点，以该双亲节点为根再访问它的右子树，
// 它的右子树又是先访问它的左子树，然后右子树最后根
// 最后直到根的左子树访问完了之后再访问右子树，最后再访问根
// 其实都是访问以每一颗子树为根的节点，只是时机不同
//
void PosOrder(BTree* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	PosOrder(root->left);
	PosOrder(root->right);
	printf("%d ", root->data);
}

后序 NULL NULL 4 NULL 2 NULL NULL 5 NULL NULL 6 3 1

今天的树与二叉树就基本概念分享到这里了，各位再见。