哈希表的实现
哈希表概念
二叉搜索树具有对数时间的表现,但这样的表现建立在一个假设上:输入的数据有足够的随机性。哈希表又名散列表,在插入、删除、搜索等操作上具有「常数平均时间」的表现,而且这种表现是以统计为基础,不需依赖输入元素的随机性。
听起来似乎不可能,倒也不是,例如:
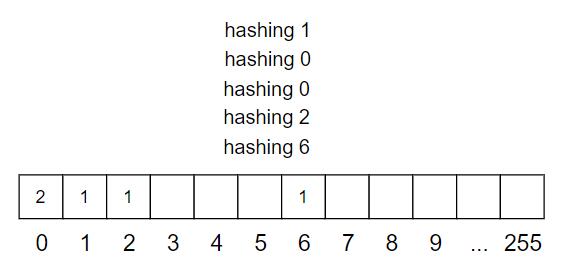
假设所有元素都是 8-bits 的正整数,范围 0~255,那么简单得使用一个数组就可以满足上述要求。首先配置一个数组 Q,拥有 256 个元素,索引号码 0~255,初始值全部为 0。每一个元素值代表相应的元素的出现次数。如果插入元素 i,就执行 Q[i]++,如果删除元素 i,就执行 Q[i]--,如果查找元素 i,就看 Q[i] 是否为 0。
这个方法有两个很严重的问题。
- 如果元素是 32-bits,数组的大小就是 2 32 = 4 G B 2^{32} = 4 GB 232=4GB,这就太大了,更不用说 64-bits 的数了
- 如果元素类型是字符串而非整数,就需要某种方法,使其可用作数组的索引
散列函数
如何避免使用一个太大的数组,以及如何将字符串转化为数组的索引呢?一种常见的方法就是使用某种映射函数,将某一元素映射为一个「大小可接受的索引」,这样的函数称为散列函数。
散列函数应有以下特性:
- 函数的定义域必须包含需要存储的全部关键字,当散列表有 m 个地址时,其值域在 0 到 m - 1 之间
- 函数计算出来的地址能均匀分布在整个空间
直接定址法
取关键字的某个线性函数为散列地址: H a s h ( K e y ) = A ∗ K e y + B Hash(Key) = A * Key + B Hash(Key)=A∗Key+B
优点:简单、均匀
缺点:需要事先知道关键字的分布情况
使用场景:数据范围比较集中的情况
除留余数法
设散列表的索引个数为 m,取一个不大于 m,但最接近 m 的质数 p 最为除数,按照散列函数: H a s h ( K e y ) = k e y Hash(Key) = key % p Hash(Key)=key,将关键字转化为哈希地址
平方取中法
假设关键字为 1230,它的平方是 1512900,取中间的 3 位 129 作为哈希地址;
再比如关键字为 321,它的平方是 103041,取中间的 3 位 304(或 30)作为哈希地址。
哈希冲突
使用散列函数会带来一个问题:可能有不同的元素被映射到相同的位置。这无法避免,因为元素个数大于数组的容量,这便是「哈希冲突」。解决冲突问题的方法有很有,包括线性探测、二次探测、开散列等。
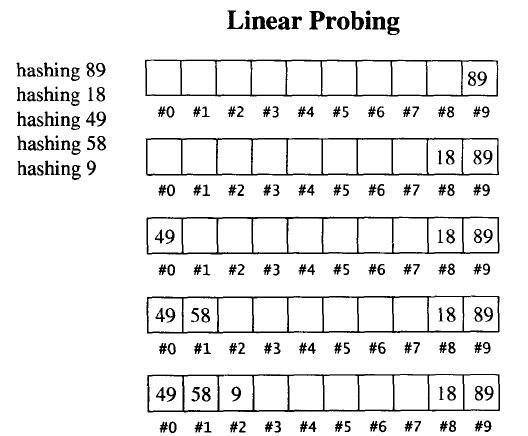
线性探测
当散列函数计算出某个元素的插入位置,而该位置上已有其他元素了。最简单的方法就是向下一一寻找(到达尾端,就从头开始找),直到找到一个可用位置。
进行元素搜索时同理,如果散列函数计算出来的位置上的元素值与目标不符,就向下一一寻找,直到找到目标值或遇到空。
至于元素的删除,必须采用伪删除,即只标记删除记号,实际删除操作在哈希表重新整理时再进行。这是因为哈希表中的每一个元素不仅表示它自己,也影响到其他元素的位置。
从上述插入过程我们可以看出,当哈希表中元素变多时,发生冲突的概率也变大了。由此,我们引出哈希表一个重要概念:负载因子。
负载因子定义为:Q = 表中元素个数 / 哈希表的长度
- 负载因子越大,剩余可用空间越少,发生冲突可能越大
- 负载因子越小,剩余可用空间越多,发生冲突可能越小,同时空间浪费更多
因此,控制负载因子是个非常重要的事。对于开放定址法(发生了冲突,就找下一个可用位置),负载因子应控制在 0.7~0.8 以下。超过 0.8,查找时的 CPU 缓存不命中按照指数曲线上升。
二次探测
线性探测的缺陷是产生冲突的数据会堆在一起,这与其找下一个空位置的方式有关,它找空位置的方式是挨着往后逐个去找。二次探测主要用来解决数据堆积的问题,其命名由来是因为解决碰撞问题的方程式 F ( i ) = i 2 F(i) = i^2 F(i)=i2 是个二次方程式。
更具体地说,如果散列函数计算出新元素的位置为 H,而该位置实际已被使用,那么将尝试 H + 1 2 , H + 2 2 , H + 3 2 , . . . , H + i 2 H + 1^2, H + 2^2, H + 3^2, ... , H + i^2 H+12,H+22,H+32,...,H+i2,而不是像线性探测那样依次尝试 H + 1 , H + 2 , H + 3 , . . . , H + i H + 1, H + 2, H + 3, ... , H + i H+1,H+2,H+3,...,H+i。
大量实验表明:当表格大小为质数,而且保持负载因子在 0.5 以下(超过 0.5 就重新配置),那么就可以确定每插入一个新元素所需要的探测次数不超过 2。
链地址法
这种方法是在每一个表格元素中维护一个链表,在呢个链表上执行元素的插入、查询、删除等操作。这时表格内的每个单元不再只有一个节点,而可能有多个节点。
节点的定义:
template <class Value>
struct __hashtable_node {
__hashtable_node* next;
Value val;
};
哈希表的实现
闭散列
接口总览
template <class K, class V>
class HashTable {
struct Elem {
pair<K, V> _kv;
State _state = EMPTY;
};
public:
Elem* Find(const K& key);
bool Insert(const pair<K, V>& kv);
bool Erase(const K& key);
private:
vector<Elem> _table;
size_t _n = 0;
};
节点的结构
因为在闭散列的哈希表中的每一个元素不仅表示它自己,也影响到其他元素的位置。所以要使用伪删除,我们使用一个变量来表示。
/// @brief 标记每个位置状态
enum State {
EMPTY, // 空
EXIST, // 有数据
DELETE // 有数据,但已被删除
};
哈希表的节点结构,不仅存储数据,还存储状态。
/// @brief 哈希表的节点
struct Elem {
pair<K, V> _kv; // 存储数据
State _state; // 存储状态
};
查找
查找的思路比较简单:
- 利用散列函数获取映射后的索引
- 遍历数组看是否存在,直到遇到空表示查找失败
/// @brief 查找指定 key
/// @param key 待查找节点的 key 值
/// @return 找到返回节点的指针,没找到返回空指针
Elem* Find(const K& key) {
if (_table.empty()) {
return nullptr;
}
// 使用除留余数法的简化版本,并没有寻找质数
// 同时,该版本只能用于正整数,对于字符串等需使用其他散列函数
size_t start = key % _table.size();
size_t index = start;
size_t i = 1;
// 直到找到空位置停止
while (_table[index]._state != EMPTY) {
if (_table[index]._state == EXIST && _table[index]._kv.first == key) {
return &_table[index];
}
index = start + i;
index %= _table.size();
++i;
// 判断是否重复查找
if (index == start) {
return nullptr;
}
}
return nullptr;
}
在上面代码的查找过程中,加了句用于判断是否重复查找的代码。理论上上述代码不会出现所有的位置都有数据,查找不存在的数据陷入死循环的情况,因为哈希表会扩容,闭散列下负载因子不会到 1。
但假如,我们插入了 5 个数据,又删除了它们,之后又插入了 5 个数据,将 10 个初始位置都变为非 EMPTY。此时我们查找的值不存在的话,是会陷入死循环的。
插入
插入的过程稍微复杂一些:
- 首先检查待插入的 key 值是否存在
- 其次需要检查是否需要扩容
- 使用线性探测方式将节点插入
/// @brief 插入节点
/// @param kv 待插入的节点
/// @return 插入成功返回 true,失败返回 false
bool Insert(const pair<K, V>& kv) {
// 检查是否已经存在
Elem* res = Find(kv.first);
if (res != nullptr) {
return false;
}
// 看是否需要扩容
if (_table.empty()) {
_table.resize(10);
} else if (_n > 0.7 * _table.size()) { // 变化一下负载因子计算,可以避免使用除法
HashTable backUp;
backUp._table.resize(2 * _table.size());
for (auto& [k, s] : _table) {
// C++ 17 的结构化绑定
// k 绑定 _kv,s 绑定 _state
if (s == EXIST) {
backUp.Insert(k);
}
}
// 交换这两个哈希表,现代写法
_table.swap(backUp._table);
}
// 将数据插入
size_t start = kv.first % _table.size();
size_t index = start;
size_t i = 1;
// 找一个可以插入的位置
while (_table[index]._state == EXIST) {
index = start + i;
index %= _table.size();
++i;
}
_table[index]._kv = kv;
_table[index]._state = EXIST;
++_n;
return true;
}
删除
删除的过程非常简单:
- 查找指定 key
- 找到了就将其状态设为 DELETE,并减少表中元素个数
/// @brief 删除指定 key 值
/// @param key 待删除节点的 key
/// @return 删除成功返回 true,失败返回 false
bool Erase(const K& key) {
Elem* res = Find(key);
if (res != nullptr) {
res->_state = DELETE;
--_n;
return true;
}
return false;
}
开散列
接口总览
template <class K, class V>
class HashTable {
struct Elem {
Elem(const pair<K, V>& kv)
: _kv(kv)
, _next(nullptr)
{}
pair<K, V> _kv;
Elem* _next;
};
public:
Elem* Find(const K& key);
bool Insert(const pair<K, V>& kv);
bool Erase(const K& key);
private:
vector<Elem*> _table;
size_t _n = 0;
};
节点的结构
使用链地址法解决哈希冲突就不再需要伪删除了,但需要一个指针,指向相同索引的下一个节点。
/// @brief 哈希表的节点
struct Elem {
Elem(const pair<K, V>& kv)
: _kv(kv)
, _next(nullptr)
{}
pair<K, V> _kv; // 存储数据
Elem* _next; // 存在下一节点地址
};
查找
查找的实现比较简单:
- 利用散列函数获取映射后的索引
- 遍历该索引位置的链表
/// @brief 查找指定 key
/// @param key 待查找节点的 key 值
/// @return 找到返回节点的指针,没找到返回空指针
Elem* Find(const K& key) {
if (_table.empty()) {
return nullptr;
}
size_t index = key % _table.size();
Elem* cur = _table[index];
// 遍历该位置链表
while (cur != nullptr) {
if (cur->_kv.first == key) {
return cur;
}
cur = cur->_next;
}
return nullptr;
}
插入
开散列下的插入比闭散列简单:
- 首先检查待插入的 key 值是否存在
- 其次需要检查是否需要扩容
- 将新节点以头插方式插入
/// @brief 插入节点
/// @param kv 待插入的节点
/// @return 插入成功返回 true,失败返回 false
bool Insert(const pair<K, V>& kv) {
// 检查是否已经存在
Elem* res = Find(kv.first);
if (res != nullptr) {
return false;
}
// 检查是否需要扩容
if (_table.size() == _n) {
vector<Elem*> backUp;
size_t newSize = _table.size() == 0 ? 10 : 2 * _table.size();
backUp.resize(newSize);
// 遍历原哈希表,将所有节点插入新表
for (int i = 0; i < _table.size(); ++i) {
Elem* cur = _table[i];
while (cur != nullptr) {
// 取原哈希表的节点放在新表上,不用重新申请节点
Elem* tmp = cur->_next;
size_t index = cur->_kv.first % backUp.size();
cur->_next = backUp[index];
backUp[index] = cur;
cur = tmp;
}
_table[i] = nullptr;
}
_table.swap(backUp);
}
// 将新节点以头插的方式插入
size_t index = kv.first % _table.size();
Elem* newElem = new Elem(kv);
newElem->_next = _table[index];
_table[index] = newElem;
++_n;
return true;
}
删除
开散列的删除与闭散列有些许不同:
- 获取 key 对应的索引
- 遍历该位置链表,找到就删除
/// @brief 删除指定 key 值
/// @param key 待删除节点的 key
/// @return 删除成功返回 true,失败返回 false
bool Erase(const K& key) {
size_t index = key % _table.size();
Elem* prev = nullptr;
Elem* cur = _table[index];
while (cur != nullptr) {
if (cur->_kv.first == key) {
if (prev == nullptr) {
// 是该位置第一个节点
_table[index] = cur->_next;
} else {
prev->_next = cur->_next;
}
delete cur; // 释放该节点
--_n;
return true;
}
prev = cur;
cur = cur->_next;
}
return false;
}