论文笔记 | 标准误聚类问题
关于标准误的选择,如是否选择稳健性标准误、是否采取聚类标准误。之前一直是困惑的,惯用的做法是类似主题的文献做法。所以这一次,借计量经济学课程之故,较深入学习了标准误的选择问题。
在开始之前推荐一个知乎博主。他阅读了很多top期刊的paper,然后平均以一周一更新的频率分享,几乎不中断。倾佩他认真专注以及坚持分享的style~ 知乎-无宇的主页
下面是这篇博客阅读的文献和一些文章
[1] (2009,RFS) -Estimating Standard Errors in Finance Panel Data Sets Comparing Approaches
[2] (JFE,2011)- Simple formulas for standard errors that cluster by both firm and time
3- Robust Inference With Multiway Clustering
[4] (QJE,2023) -When should you adjust standard errors for clustering
[5] [聚类稳健标准误_CSDN_celine0227] ( https://blog.csdn.net/celine0227/article/details/124405756)
这里写目录标题
- RFS-2009
-
- 1、残差项的iid
- 2、违背残差项iid的情形下,有效性违背的两种情况:
- 3、自相关情境下,标准误如何受到影响:
- 4、存在公司固定效应下,如何解决自相关对标准误有效性的影响:
- 5、存在时间固定效应下,如何解决自相关对标准误有效性的影响:
- 6、同时存在固定的企业效应和时间效应,如何解决自相关对标准误有效性的影响:
- 7、存在暂时公司效应时,如何解决自相关对标准误有效性的影响:
- 8、总结
- JFE-2011
-
- 1、整体介绍
- 2、本文探讨了何时采用双聚类偏差。
- 3、本文探讨了数据集中公司和时间维度数量对于聚类层面的影响。
- 5、聚类数量对标准误方差的影响
- 6、持续共同冲击的影响
- 7、蒙特卡洛实验的结果
- 8、结论
- JBES-2011
- QJE-2023
-
- 1、论文的聚类框架
- 2、传统聚类标准误调整的几个误解
- 3、传统聚类框架与本文框架的区别
- 4、结论
本篇博客只是对各篇论文学习的总结
RFS-2009
摘要:在公司融资和资产定价实证工作中,研究人员经常面对面板数据。在这些数据集中,残差可能跨公司或跨时间相关,OLS标准误差可能存在偏差。从历史上看,这两个文献中的研究人员对这个问题使用了不同的解决方案。本文研究了文献中使用的不同方法,并解释了不同的方法何时产生相同(和正确的)标准误差以及何时发散。其目的是提供直觉,说明为什么不同的方法有时会给出不同的答案,并为研究人员提供使用指导。
1、残差项的iid
残差项在iid(独立同分布,意味着残差间的协方差为0,残差同方差)。
这种情形下,估计量及其方差为
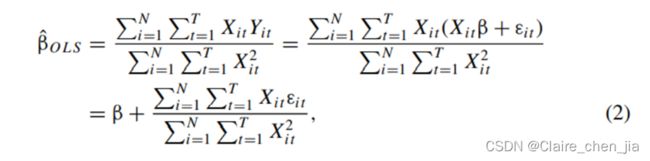
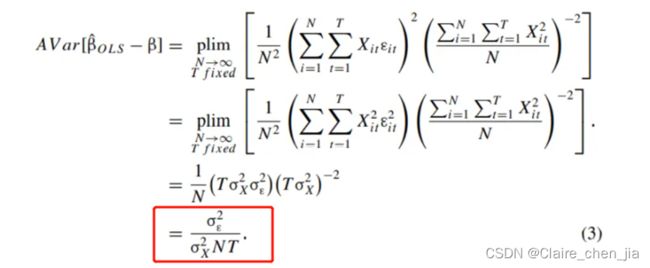
2、违背残差项iid的情形下,有效性违背的两种情况:
(1)异方差:残差间的协方差为0,但残差是异方差。考虑到个体差异,我们默认认为残差间存在异质性,所以在没有自相关的情形下,常用White的稳健性标准误。
(2)自相关:残差间的协方差不为0。
以公司-年的面板数据结构为例,本篇作者讨论了两种自相关情形:
- 公司固定效应:同一公司内的不同年份观测值的自相关(如A公司的创新文化在各年一直都存在,B公司的激进主义在各年一直都存在);
- 时间固定效应:同一年份内在不同公司观测值的自相关(如今年宏观政策对所有公司产生影响,使得公司间存在相关)
由于我们最常规情形下也会选择稳健性标准误,所以本文主要讨论的是聚类标准误的情形。
3、自相关情境下,标准误如何受到影响:
存在公司固定效应自相关情境下,OLS的一致性还保持,但有效性受到损害(信息量没有充分利用)。

这个时候,同一公司内的残差间的协方差不为0,观测值的协方差也不为0.
对比(3)和(7),如果我们不考虑公司固定效应的自相关问题,而直接采用iid假设的标准误,会使得标准误变小。从公式可以看出。但深层次原因是iid情况下,认为的每个观测值信息是不同的。但事实上每个公司内存在一部分相同的信息,并没有提供增量的部分,导致没有考虑自相关下,低估了标准误。这样会使得t值变大,容易接受论文假设,导致第二类错误(存伪)。
4、存在公司固定效应下,如何解决自相关对标准误有效性的影响:
可以采用聚类在公司层面的标准误。
(1)聚类标准误:估算出聚类内残差的相关性
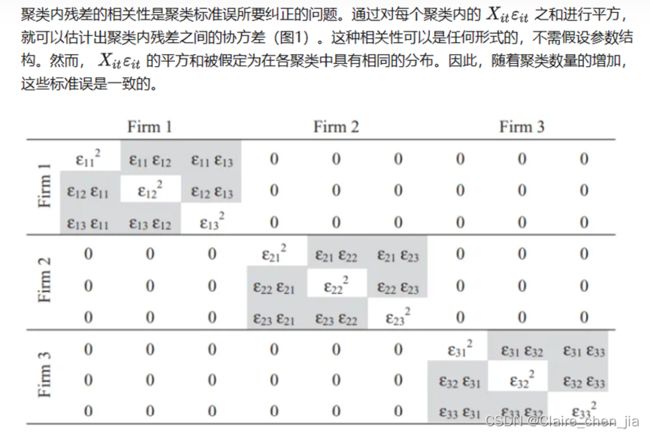
(2)Fama-MacBeth标准误不可以:仅适用于时间固定效应,不适用于公司固定效应。研究者运行T个横向回归,T次估计的平均值就是系数估计值。这种方法不能够解决具有公司固定效应的自相关,但是可以解决具有时间固定效应的自相关。原因是即使是分开每一年的公司估计β,但是每一期估计的β夹杂了公司固定效应的信息,从而导致公司固定效应的影响还在。但年份不会,因为年份不重叠。

(3)Newey-West标准误存在低估:估计同一聚类中滞后残差之间的相关性。由于方程采用对协方差的加权小于1,所以标准误的估计相比聚类标准误仍然存在低估(公式(7)和(14)的对比)。

5、存在时间固定效应下,如何解决自相关对标准误有效性的影响:
可以采用聚类在时间的标准误和Fama-MacBeth标准误。
6、同时存在固定的企业效应和时间效应,如何解决自相关对标准误有效性的影响:
在面板数据集中估计标准误的最佳方法取决于数据中非独立性的来源。对于只有企业效应的面板数据集,按企业聚类最好。如果数据只有时间效应,当年数较少时,Fama-MacBeth法比按时间聚类要好;当年数足够多时,两者一样好。这些方法使研究者对聚类内的相关形式不可知,但代价是残差必须在各聚类之间不相关。但很多时候难以满足。也就是说同时存在固定的企业效应和时间效应的情况,这种情形下,如何解决?
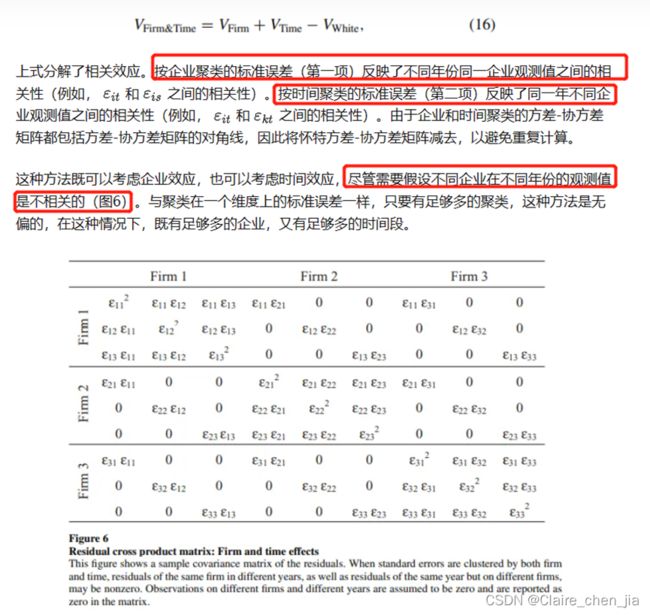
金融实证研究者解决两个相关来源的方法之一是对其中一个维度进行参数化估计(例如,通过加入虚拟变量)。由于许多面板数据集的公司数量多于年份数量,一种常见的方法是为每个时间加入虚拟变量(以吸收时间效应),然后按公司进行聚类。如果时间效应是固定的,时间虚拟变量完全消除了同一时间段内观测值之间的相关性。在这种情况下,数据中只剩下企业效应。
如果时间效应不固定,那么时间虚拟变量就不能完全消除非独立性==(例如2008年的金融危机不仅在08年产生影响,还在09年)==,即使是按企业聚类的标准误也会有偏差。由于研究者并不总是知道非独立性的精确形式,因此可能会倾向于采用不那么参数化的方法。一个解决方案是同时在两个维度上进行聚类(例如,公司和时间)。Cameron、Gelbach和Miller(2006)以及Thompson(2006)提出了以下方差-协方差矩阵的估计:
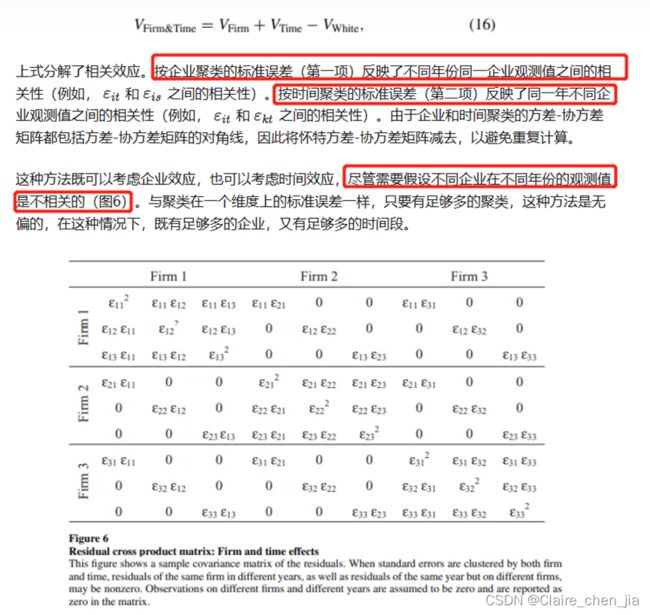
论文做了一个蒙特卡洛模拟,使用10000个观测值,按照10到1000个企业进行企业和时间的滑动变化。在同时存在两个效应时,只按照1个维度进行聚类,标准误会发生剧烈变化,但是当这个维度有更多聚类时,它的标准误与双重聚类一样。如1000个企业*10年的样本结构中,只按照公司层面的聚类和双重的聚类的拒绝率在同等水平。
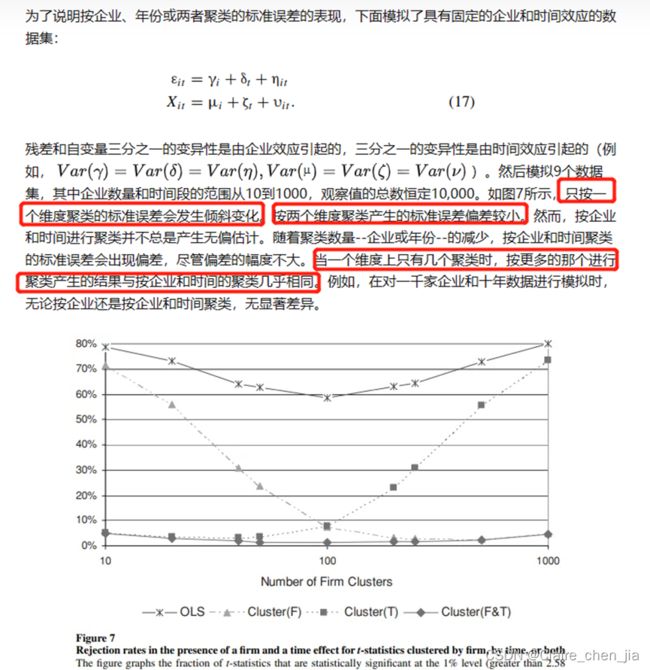
7、存在暂时公司效应时,如何解决自相关对标准误有效性的影响:
8、总结
JFE-2011
摘要:在估计财务面板回归时,通常的做法是调整跨公司或跨时间相关性的标准误差。只有当残差跨时间或跨公司相关时,这些程序才有效,但不能同时关联两者。本文表明,计算标准误差非常容易,==这些标准误差对两个维度(例如公司和时间)上的同时相关性具有鲁棒性。协方差估计量等于按公司聚类的估计量加上按时间聚类的估计量减去通常的异方差稳健性普通最小二乘 (OLS) 协方差矩阵。==任何带有聚类命令的统计包都可用于轻松计算这些标准误差。
1、整体介绍
这篇论文,是在RFS-2009的基础上,进一步考虑公司固定效应和时间固定效应同时存在的情形,并更进一步介绍了它的实现。



2、本文探讨了何时采用双聚类偏差。
双聚类在具有以下特征的数据集中可能最有用:回归误差包括重要的时间和公司成分,回归变量本身包括重要的公司和时间成分,公司和时间段的数量没有太大差异。因此,如果回归变量随时间变化而不是随公司变化,那么按时间聚类可能就足够好了,而双聚类可能不会产生很大的差异。如果公司数量远远超过时间段,则按时间聚类可以消除大部分偏差,除非公司内部相关性远大于时间段内的相关性。
本文考虑持续共同冲击有关的特殊情况。即不同时期不同公司间的相关性。standard errors that correct for persistent common shocks will tend to be biased downward. Eliminating the bias requires a large number of time periods.

3、本文探讨了数据集中公司和时间维度数量对于聚类层面的影响。
一般的观点是,在其他条件相同的情况下,沿观测值较少的维度聚类更为重要。如果维度极其不平衡,我们根本不需要双重聚类。。
例子:如果我们有一个包含10家公司和 1000个时间段的样本,那么更大的偏差减少可能来自按公司聚类。本文认为是,当一个维度是固定数量,但另外一个维度趋向于无穷。如果采用无穷的那个维度聚类时,观测值(聚类维度的数目)无限大,聚类内的个体会更少,使得这个维度内的每个聚类内的协方差收敛于0,进而等同于每个聚类就是每个随机分配的个体,不存在自相关问题。
==需要明确的是,聚类的效果是由每个维度内的观测值数量与内部观测值之间的相关性大小之间的相互作用决定的。==如果没有公司效应,即给定公司的观察在各个时间段之间是不相关的,那么我们不需要按公司聚类,即使有 1000 个时间段并且只有十家公司。但是,如果数据具有显著的公司和时间效应,则沿观测值较少的维度聚类可能更为重要。
该分析表明,当公司数量和时间段相差不大时,双聚类最为重要。例如,Fama和French(2000)在一个包含数千家公司和大约35年年度会计数据的小组中预测了公司层面的盈利能力。在这种情况下,按时间聚类可能已经足够好了,因为没有按公司聚类而导致的偏差增加可能很小。



5、聚类数量对标准误方差的影响
对于聚类标准误差,标准误差估计值的方差随着聚类数量(聚类维度的数量)的减少而变大。聚类标准误差是通过跨聚类求平均值来估计的。较少的聚类意味着平均值中的项数量较少,因此估计误差较大。
考虑一下研究人员在从单聚类标准误差到双聚类标准误差时看到非常不同的结果的情况。研究人员可能会将此作为证据,证明沿着两个维度进行聚类很重要。但是,如果时间维度或公司维度中的聚类太少,则双聚类标准误差估计值将是噪声的。不同的结果可能是杂散的,并且是由于噪声。因此,==只有当我们在两个维度上都有足够的聚类时,双聚类才有意义。==在实践中我们需要多少个集群?

6、持续共同冲击的影响
关于持续共同冲击造成的偏差有两个有用事实:它随着相关性的大小而增加,并且随着样本变大而消失。
因此,我们预计当相关性接近于零且样本量较大时,这些聚类标准误差表现良好。当然,如果相关性很低,那么我们可以忽略它们并使用更简单的公式。这些标准误差明确首选的唯一情况是相关性显著且样本量大到足以纠正偏差。我进行蒙特卡洛斯检查,看看样本需要多大。
7、蒙特卡洛实验的结果
蒙特卡洛斯通常支持使用稳健的标准误差。单聚类标准误差无法处理一个回归量具有显著时间效应而另一个回归量具有显著的公司效应的回归。如果我们愿意在 10% 大小的测试中接受高达 5% 的错误拒绝,那么只要我们对公司和时间都有超过 25 个观察结果,双聚类就会很好地工作(换言之,聚类维度数量至少要有25个)。纠正持续的共同冲击需要 50 到 100 个时间段。
8、结论
本文推导出了易于计算的标准误差公式,这些公式按公司和时间进行聚类。统计理论和蒙特卡洛结果都表明,同时按公司和时间进行聚类会导致金融小组的推断更加准确。蒙特卡罗实验表明,只要我们不允许持续的共同冲击,当我们至少有25家公司和时间段时,对公司和时间的聚类就足够了。但是,允许持续的常见冲击需要更多的时间段。
#JBES-2011
摘要:在这篇文章中,我们提出了一个方差估计的OLS估计量以及非线性估计量,如logit, probit,和GMM。当存在非嵌套的双向或多维聚类时,此方差估计器支持cluster-robust inference。方差估计量扩展了the standard cluster robust variance estimator or sandwich estimator for one-way clustering(例如,Liang和Zeger 1986;Arellano 1987),并依赖于类似的相对较弱的分布假设。我们的方法很容易在统计包中实现,例如Stata和SAS,当存在单向聚类时,它们已经提供了cluster robust的标准误差。通过对双向随机效应模型的蒙特卡罗分析,证明了该方法的有效性;对安慰剂定律的蒙特卡洛分析,将Bertrand, Duflo和Mullainathan(2004)的状态-年效应例子扩展到二维;并应用于实证文献中存在双向聚类的研究。
这篇文章提供了实现多维聚类的stata包,并且建议当样本数量过小,导致维度数量小的情况下,建议对标准误差和Wald测试临界值进行调整。本文给出的最小维度标准是10,与JFE有所差别。
JBES-2011
摘要:在这篇文章中,我们提出了一个方差估计的OLS估计量以及非线性估计量,如logit, probit,和GMM。当存在非嵌套的双向或多维聚类时,此方差估计器支持cluster-robust inference。方差估计量扩展了the standard cluster robust variance estimator or sandwich estimator for one-way clustering(例如,Liang和Zeger 1986;Arellano 1987),并依赖于类似的相对较弱的分布假设。我们的方法很容易在统计包中实现,例如Stata和SAS,当存在单向聚类时,它们已经提供了cluster robust的标准误差。通过对双向随机效应模型的蒙特卡罗分析,证明了该方法的有效性;对安慰剂定律的蒙特卡洛分析,将Bertrand, Duflo和Mullainathan(2004)的状态-年效应例子扩展到二维;并应用于实证文献中存在双向聚类的研究。
这篇文章提供了实现多维聚类的stata包,并且建议当样本数量过小,导致维度数量小的情况下,建议对标准误差和Wald测试临界值进行调整。本文给出的最小维度标准是10,与JFE有所差别。
QJE-2023
摘要:聚类标准误差,由地理等因素定义的聚类,在经济学和许多其他学科的实证研究中很普遍。从形式上讲,聚类标准误差通过从具有未观察到的聚类级组件的数据生成过程中对结果变量进行采样而调整引起的相关性。然而,聚类的标准计量经济学框架留下了重要的问题:(i)为什么我们在某些方面调整聚类的标准误差而不在其他方面,例如,按州而不是按性别,在观察性研究中而不是在完全随机的实验中?(ii) 如果我们在总体中观察到大部分聚类,聚类方差估计量是否有效?(iii) 在哪些情况下,是否以及如何分组的选择会有所不同?==我们使用一种新的框架来对平均处理效果进行聚类推断,从而解决这些问题和其他问题。除了通用抽样组件外,新框架还包含一个设计组件,该组件考虑了处理分配机制在估计器上引起的变异性。我们表明,当样本中的聚类数量是总体中聚类数的不可忽略的一部分时,传统的聚类标准误差可能会严重膨胀,并提出新的方差估计量来纠正这种偏差。
这篇文章是在以往关于聚类问题讨论上的突破,使用两步的抽样设计的思路来讨论是否及何时需要使用聚类的标准误差。
1、论文的聚类框架
本文提出的聚类框架与标准框架的不同之处在于,它包括一个设计部分,即考虑到处理分配中的聚类间变化。本文认为,这个新的设计组件是很重要的,因为处理分配中的聚类间差异常常促使我们在经验研究中使用聚类标准误差。此外,本文框架将关注的焦点从无限超级总体/数据生成过程的特征转移到为手头的有限(但可能很大)总体定义的平均处理效应。由于这种转变,抽样过程和处理分配机制只决定了正确的聚类水平;结果变量中聚类水平的非观察成分存在与聚类水平的选择无关。此外,通过关注有限总体(在数据中可能被完全或大量抽样),本文获得的标准误差比那些旨在衡量无限超级总体特征不确定性的标准误差小。在本文提出的框架下,推导出最小二乘法和固定效应估计的大样本方差,并表明它们与稳健方差和聚类方差都有很大不同。==本文提出了两个大样本方差的估计方法,一个是分析性的,一个是基于再抽样(bootstrap)方法的。==对于美国收入的应用,本文建议产生的标准误差比稳健标准误差大得多,但比传统版本的聚类标准误差小得多。
2、传统聚类标准误调整的几个误解
本文用该框架来强调围绕聚类调整的三个常见误解。==第一个误解是,对聚类的需求取决于属于同一聚类单位的残差之间是否存在非零相关性。==本文表明,这种相关性存在并不意味着需要使用聚类调整。第二个误解是,在不需要聚类调整的情况下,使用聚类调整是没有坏处的,其含义是,如果聚类标准误差有区别,就应该聚类。为了说明这两种说法都是不正确的,请考虑下面这个简单例子。假设根据感兴趣总体的随机抽样,用一个变量的样本平均值来估计它的总体平均值。假设总体可以被划分为多个聚类,如地理单位。如果结果在聚类中是正相关的,那么聚类方差将大于稳健方差。然而,标准抽样理论直接意味着,如果单位是从总体中随机抽样的,就没有必要进行聚类。在这种情况下,聚类的危害在于置信区间会不必要地保守,可能会有很大的差距。第三个误解是,研究人员只有两种选择:要么完全调整聚类并使用聚类标准误差,要么根本不调整标准误差而使用稳健标准误差。本文提出了新的方差估计器,可以比稳健方差估计和聚类方差估计都大幅提高准确性。
3、传统聚类框架与本文框架的区别
在传统的基于模型的计量经济学框架中,研究者对结果变量的模型误差分量结构采取了立场。例如,假设按照Moulton(1986 ,1987 )的说法,研究者提出了一个随机效应模型,在州一级有随机效应。在这种情况下,一个重复抽样的思想实验需要对每个样本,从其分布中抽取不同的状态随机效应值。这种基于模型的方法意味着,如果使用样本平均值来估计总体平均值,即使样本是个体的随机样本而不是聚类样本,也需要在州一级对标准误差进行聚类。基于模型的计量经济学框架在聚类方面的一个缺点是,经验研究者需要对其模型的误差成分的结构进行表态。
计量经济学文献中经常引用的第二个聚类框架是以抽样机制为动机,在第一阶段从一个无限大的总体中随机选择聚类,然后在第二阶段从被抽样的聚类中随机抽出单位(或保持一个聚类中的所有单位)。虽然这个框架适合于其发源地——调查分析中的一些应用(Kish,1995 ;Thompson,2012 ),但本文认为它不适合经济学家和其他社会科学家分析的许多数据集。在经济学的许多应用中,研究人员从他们感兴趣的所有聚类中观察单位,例如美国的所有州,基于随机抽样的框架并不适用于大量聚类总体中的一小部分。
上述两种传统的聚类推理框架都没有完全纳入聚类的设计方面。缺少设计成分是使它们不适合于推断处理效应的原因。为了深入了解分配机制对处理效应估计标准误差的重要性,请考虑一个环境,即从总体中随机抽样的个体,但处理是在聚类水平上分配的,同一聚类中的所有人都有相同的处理值。假设所关注的数量是总体平均处理效应。对处理的聚类分配等同于对潜在结果的聚类抽样。由于感兴趣的参数取决于潜在结果的平均值,而这些结果是以聚类方式抽样的,因此在这种情况下,即使个别观察值是随机抽样的,也需要标准误差聚类。在这种情况下,本文聚类推断框架在精神上与上一段描述的抽样框架很接近,但它明确地包含了一个设计部分。
==通过将注意力从结果数据生成过程的参数转移到手头总体的平均处理效应上,应用本文建议的研究者不需要对结果变量模型的误差分量结构采取立场来计算标准误差。==相反,所有与平均处理效应有关的估计值都是由抽样机制和分配机制产生的,前者从总体中提取样本,后者决定哪些单位接受处理。本文认为这是该框架在难以证明特定误差成分结构情况下的内在优势。

4、结论
本文提出了一个研究框架,旨在解决一个与经验实践相关的核心问题:应该在什么时候以及如何对标准误差进行聚类。与Abadie等(2020)一样,本文将注意力从对数据生成过程(即无限的超级总体)的估计转移到对手头有限总体的平均处理效应的估计。==本文表明,在这个框架中,关于何时以及如何进行标准误差聚类的决定只取决于抽样和分配过程的性质,而不取决于结果变量中是否存在聚类内误差成分。本文推导出在聚类抽样的情况下,平均处理效应的OLS和FE估计的大样本方差表达式,在这种情况下,聚类中的分配是随机的,分配概率在不同聚类中可能有所不同。在这种情况下,本文证明稳健标准误差可能太小,而传统的聚类标准误差可能不必要地大。本文提出了两个新程序,即CCV和TSCB,可以用来在有大聚类和聚类中处理分配有足够变化的情况下计算更精确的标准误差(这样聚类中的平均处理效应可以被精确估计)。==虽然CCV和TSCB是为这一特定环境设计的,但该框架的一般原则对其他环境和估计者仍然有效。如果抽样不是聚类的,标准误差应该在处理分配水平上聚类,因为感兴趣的估计值取决于潜在结果,而潜在结果的抽样只由分配机制决定。当被抽样聚类的比例不可忽略,而且各聚类的平均处理效应存在差异时,传统聚类标准误差可能会出现偏差,本文提供了一个分析框架,可以用来得出适当的标准误差。当抽样和分配是随机的,无论总体中各单位结果的协方差结构如何,聚类标准误差都是不合适的。在这种情况下,如果存在大量的处理效应异质性,并且样本代表了所关注总体的很大一部分,那么稳健标准误差在大样本中是保守的。这种偏差可以用Abadie等(2020)的方法来纠正。为本文所介绍的抽样和分配过程以外的抽样和分配过程推导出标准误差公式是未来研究的一个重要途径。Rambachan和Roth(2022) 是这个方向的最新贡献。此外,本文将分析限制在线性估计(最小二乘法和固定效应)。Xu(2019) 使用本文的思想和框架来研究非线性估计背景下的聚类问题。