蓝桥杯 - 皮亚诺曲线距离
题目描述
皮亚诺曲线是一条平面内的曲线。
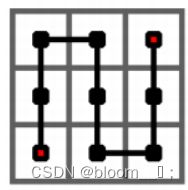
下图给出了皮亚诺曲线的 1 1 1 阶情形,它是从左下角出发,经过一个 3 × 3 3×3 3×3 的方格中的每一个格子,最终到达右上角的一条曲线。
下图给出了皮亚诺曲线的 2 2 2 阶情形,它是经过一个 3 2 × 3 2 3^2×3^2 32×32 的方格中的每一个格子的一条曲线。它是将 1 1 1 阶曲线的每个方格由 1 1 1 阶曲线替换而成。
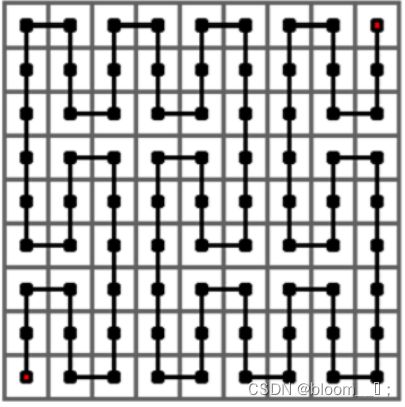
下图给出了皮亚诺曲线的 3 3 3 阶情形,它是经过一个 3 3 × 3 3 3^3×3^3 33×33 的方格中的每一个格子的一条曲线。它是将 2 2 2 阶曲线的每个方格由 1 1 1阶曲线替换而成。
皮亚诺曲线总是从左下角开始出发,最终到达右上角。
我们将这些格子放到坐标系中,对于 k k k 阶皮亚诺曲线,左下角的坐标是 ( 0 , 0 ) (0,0) (0,0),右上角坐标是 ( 3 k − 1 , 3 k − 1 ) (3^k−1,3^k−1) (3k−1,3k−1),右下角坐标是 ( 3 k − 1 , 0 ) (3^k−1,0) (3k−1,0),左上角坐标是 ( 0 , 3 k − 1 ) (0,3^k−1) (0,3k−1)。
给定 kk 阶皮亚诺曲线上的两个点的坐标,请问这两个点之间,如果沿着皮亚诺曲线走,距离是到少?
输入描述
输入的第一行包含一个正整数 kk,皮亚诺曲线的阶数。
第二行包含两个整数 x 1 , y 1 x1,y1 x1,y1,表示第一个点的坐标。
第三行包含两个整数 x 2 , y 2 x2,y2 x2,y2,表示第二个点的坐标。
其中有 ,
0 ≤ k ≤ 100 0 ≤ x 1 , y 1 , x 2 , y 2 < 3 k x 1 , y 1 , x 2 , y 2 ≤ 1 0 18 0≤k≤100\\ 0≤x1,y1,x2,y2<3^k\\ x1,y1,x2,y2≤10^{18} 0≤k≤1000≤x1,y1,x2,y2<3kx1,y1,x2,y2≤1018
数据保证答案不超过 1 0 18 10^{18} 1018。
输出描述
输出一个整数,表示给定的两个点之间的距离。
输入输出样例
示例
输入
1
0 0
2 2
输出
8
运行限制
最大运行时间:1s
最大运行内存: 128M
解题思路
这题可以和分形之城对应起来做,这题是知道两点就距离,分形之城是知道两点到起点的距离求两点距离
acwing-分形之城
求两点的距离可以考虑先求两点各自到起点的距离然后再相减。
这题可以将当前图像看成 9 9 9 块 k − 1 k-1 k−1 阶的图像通过 水平、垂直翻转 而来,对于每一阶,变化方式一样,计算方式也是一样的。
先计算当前坐标在当前阶 9 9 9 块中的哪一块,根据一阶的顺序这块之前有多少块,根据阶数可以计算每一块的点数,加上前几块的点数。
剩余的就从当前块的入口作为起点,再递归下去以相同的方式求之前有多少块,有多少点数,根据二阶的情况来判断翻转方式。
对于翻转的情况需要在上一阶提前计算好坐标变换后的位置再递归到下一层进行计算。
水平翻转: [ x , y ] = [ − x , y ] [x, y]=[-x,y] [x,y]=[−x,y],这样翻转之后图像整体左移 x x x 个单位,所以用下一阶的长度来减去 x x x。
垂直翻转同理。
注:
因为这题的数据实在太大
题目说小于 1 0 18 10^{18} 1018 又小于 3 k 3^{k} 3k 有点奇怪
3 k 3^{k} 3k 的话最高 3 100 × 3 100 3^{100} \times 3^{100} 3100×3100 个点
光数字长度都有 96 96 96 个十进制位
c++需要使用高精度,我这里偷个懒用python
code
def calc(k, x, y):
if k == 0: return 0
le = pow(3, k - 1) # 每一小块的边长(一行/列的点数)
blk = le * le # 每一小块的面积(点的数量)
nx, ny = x // le, y // le # 当前坐标所在的哪一小块的坐标
mx, my = x % le, y % le # 当前坐标所在的小块内的相对坐标
if nx == 0 and ny == 0: return calc(k - 1, mx, my)
elif nx == 0 and ny == 1: return blk + calc(k - 1, le - mx - 1, my)
elif nx == 0 and ny == 2: return 2 * blk + calc(k - 1, mx, my)
elif nx == 1 and ny == 2: return 3 * blk + calc(k - 1, mx, le - my - 1)
elif nx == 1 and ny == 1: return 4 * blk + calc(k - 1, le - mx - 1, le - my - 1)
elif nx == 1 and ny == 0: return 5 * blk + calc(k - 1, mx, le - my - 1)
elif nx == 2 and ny == 0: return 6 * blk + calc(k - 1, mx, my)
elif nx == 2 and ny == 1: return 7 * blk + calc(k - 1, le - mx - 1, my)
else: return 8 * blk + calc(k - 1, mx, my)
if __name__ == '__main__':
k = int(input())
a = list(map(int, input().split()))
b = list(map(int, input().split()))
d1 = calc(k, a[0], a[1])
d2 = calc(k, b[0], b[1])
print(abs(d2 - d1))