2022CCPC湖北省赛题解ABCFJKL
2022CCPC湖北省赛题解ABCFJKL
K. Keep Eating
题意
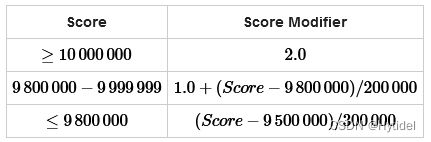
有 t ( 1 ≤ t ≤ 1 e 5 ) t\ \ (1\leq t\leq 1\mathrm{e}5) t (1≤t≤1e5)组测试数据.每组测试数据输入一个整数 n ( 0 ≤ n ≤ 1001576 ) n\ \ (0\leq n\leq 1001576) n (0≤n≤1001576)和一个实数 c ( 1.0 ≤ c ≤ 11.5 ) c\ \ (1.0\leq c\leq 11.5) c (1.0≤c≤11.5). n n n根据上述表格换算后与 c c c相加,输出结果.
代码 -> 2022CCPC湖北省赛-K(模拟)
void solve() {
double n, ans; cin >> n >> ans;
if (n >= 1e7) ans += 2;
else if (n > 9800000) ans += 1.0 + (n - 9800000) / 200000;
else ans += (n - 9500000) / 300000;
cout << fixed << setprecision(18) << max(ans, 0.0) << endl;
}
int main() {
CaseT // 单测时注释掉该行
solve();
}
B. Potion(easy version)
题意 ( 3 s 3\ \mathrm{s} 3 s)
有一容量为 ( a + b ) (a+b) (a+b)且只有一个从下往上的刻度 a a a的量杯.有两类水,若能通过若干次接水倒水使得杯中两种水的比例为 x : y x:y x:y,输出最小接水次数;否则输出 − 1 -1 −1.简单版本中,保证 a = b = 1 a=b=1 a=b=1.
有 t ( 1 ≤ t ≤ 1 e 5 ) t\ \ (1\leq t\leq 1\mathrm{e}5) t (1≤t≤1e5)组测试数据.每组测试数据输入四个整数 x , y , a , b ( 1 ≤ a , b , x , y ≤ 1 e 18 ) x,y,a,b\ \ (1\leq a,b,x,y\leq 1\mathrm{e}18) x,y,a,b (1≤a,b,x,y≤1e18).数据保证 a = b = 1 a=b=1 a=b=1.
思路
设当前第一类水的比例为 d d d,初始时 d = 0 d=0 d=0或 1 1 1.从刻度 a a a开始接满后,若接第一类水,则第一类水的比例变为 d + b a + b = d + 1 2 \dfrac{d+b}{a+b}=\dfrac{d+1}{2} a+bd+b=2d+1;若接第二类水,则第一类水的比例变为 d a + b = d 2 \dfrac{d}{a+b}=\dfrac{d}{2} a+bd=2d.
保持第一类水的比例为最简分数,规律: { d + 0 2 { d + 0 4 { d + 0 8 d + 4 8 d + 2 4 { d + 2 8 d + 6 8 d + 1 2 { d + 1 4 { d + 1 8 d + 5 8 d + 3 4 { d + 3 8 d + 7 8 \begin{cases}\dfrac{d+0}{2}\begin{cases}\dfrac{d+0}{4}\begin{cases}\dfrac{d+0}{8} \\ \dfrac{d+4}{8}\end{cases} \\ \dfrac{d+2}{4}\begin{cases}\dfrac{d+2}{8} \\ \dfrac{d+6}{8}\end{cases}\end{cases} \\ \dfrac{d+1}{2}\begin{cases}\dfrac{d+1}{4}\begin{cases}\dfrac{d+1}{8} \\ \dfrac{d+5}{8}\end{cases} \\ \dfrac{d+3}{4}\begin{cases}\dfrac{d+3}{8} \\ \dfrac{d+7}{8}\end{cases}\end{cases}\end{cases} ⎩ ⎨ ⎧2d+0⎩ ⎨ ⎧4d+0⎩ ⎨ ⎧8d+08d+44d+2⎩ ⎨ ⎧8d+28d+62d+1⎩ ⎨ ⎧4d+1⎩ ⎨ ⎧8d+18d+54d+3⎩ ⎨ ⎧8d+38d+7.
显然第 n n n次接水后第一类水的比例的分母为 2 n − 1 2^{n-1} 2n−1.
初始时 d = 0 d=0 d=0,即第一次接第二类水时,第二次显然应接第一类水,对应上表的下半部分,此时分母都为奇数.
初始时 d = 1 d=1 d=1,即第一次接第一类水时,第二次显然应接第二类水,对应上表的上半部分,此时分母都为奇数.
综上,配凑出的比例分子为奇数,分母为 2 n − 1 2^{n-1} 2n−1,接水次数为 n n n.将 x y \dfrac{x}{y} yx化为最简分数后,检查 x x x和 y y y是否为奇数, x + y x+y x+y是否是 2 2 2的幂次即可.约分的正确性见C题证明.
代码 -> 2022CCPC湖北省赛-B(找规律)
void solve() {
ll x, y, a, b; cin >> x >> y >> a >> b;
ll d = gcd(x, y);
x /= d, y /= d;
ll sum = x + y;
if ((x & 1) && (y & 1) && sum == lowbit(sum)) {
for (int i = 63; i >= 0; i--) {
if (sum >> i & 1) {
cout << i + 1 << endl;
return;
}
}
}
else cout << -1 << endl;
}
int main() {
CaseT // 单测时注释掉该行
solve();
}
C. Potion(hard version)
题意 ( 3 s 3\ \mathrm{s} 3 s)
有一容量为 ( a + b ) (a+b) (a+b)且只有一个从下往上的刻度 a a a的量杯.有两类水,若能通过若干次接水倒水使得杯中两种水的比例为 x : y x:y x:y,输出最小接水次数;否则输出 − 1 -1 −1.
有 t ( 1 ≤ t ≤ 1 e 5 ) t\ \ (1\leq t\leq 1\mathrm{e}5) t (1≤t≤1e5)组测试数据.每组测试数据输入四个整数 x , y , a , b ( 1 ≤ a , b , x , y ≤ 1 e 18 ) x,y,a,b\ \ (1\leq a,b,x,y\leq 1\mathrm{e}18) x,y,a,b (1≤a,b,x,y≤1e18).
思路
设接水次数为 ( n + 1 ) (n+1) (n+1),其中第一次为从刻度 0 0 0开始接满,其余为从刻度 a a a开始接满,显然这是最优的.
将 a b \dfrac{a}{b} ba和 x y \dfrac{x}{y} yx化为最简分数,其正确性后面证明.设 c = a + b c=a+b c=a+b.类似于B题的思路,易得第 n n n次接水后第一类水的比例的分母为 ( a + b ) n − 1 (a+b)^{n-1} (a+b)n−1,则有解的必要条件是 ( a + b ) ∣ ( x + y ) (a+b)\mid (x+y) (a+b)∣(x+y).
逆向考虑该过程,若能配置出某种比例的水,将所有操作逆序后,最终能回到一类水的初始比例为 a a a,另一类水的比例为 b b b的初始状态,此时 a + b = x + y a+b=x+y a+b=x+y.此时再回退一步,得到只有一类水比例为 a a a的初始状态.
下面构造一个方案:设当前两种水的比例为 ( x , y ) (x,y) (x,y).
(1)若当前 x x x和 y y y都非零,不妨设 x ≤ y x\leq y x≤y;否则至少有一类水的比例为 0 0 0,此时找到一组解,输出答案即可.
①若当前 ( a + b ) ∤ ( x + y ) (a+b)\not\mid(x+y) (a+b)∣(x+y),则无解.
②若 ( a + b ) ∣ ( x + y ) (a+b)\mid (x+y) (a+b)∣(x+y),求出比例系数 k = x + y a + b ∈ Z k=\dfrac{x+y}{a+b}\in\mathbb{Z} k=a+bx+y∈Z,作为该步两类水的比例之和.
(2)①若 a ∤ x a\nmid x a∤x且 a ∤ y a\nmid y a∤y,则无解,因为最终无法使得一类水的比例为 a a a.
②若 a ∣ x a\mid x a∣x,将 ( x a , k − x ) \left(\dfrac{x}{a},k-x\right) (ax,k−x)作为新的 ( x , y ) (x,y) (x,y),回到(1).
③若 a ∣ y a\mid y a∣y,将 ( y a , k − x ) \left(\dfrac{y}{a},k-x\right) (ay,k−x)作为新的 ( x , y ) (x,y) (x,y),回到(1).
下面证明该方案的正确性:
[证] 设有解,且最优解的答案为 a n s ans ans.将 a b \dfrac{a}{b} ba和 x y \dfrac{x}{y} yx都化为最简分数,由有解的必要条件: ( a + b ) ∣ ( x + y ) (a+b)\mid (x+y) (a+b)∣(x+y).
因第 n n n次接水后第一类水的比例的分母为 ( a + b ) n − 1 (a+b)^{n-1} (a+b)n−1,则 a n s ≥ log a + b ( x + y ) + 1 ans\geq \log_{a+b}(x+y)+1 ans≥loga+b(x+y)+1.
而上述方案给出了 a n s = log a + b ( x + y ) + 1 ans=\log_{a+b}(x+y)+1 ans=loga+b(x+y)+1的构造,故它是最优解.
下面证明约分的正确性:
(1)设 a b \dfrac{a}{b} ba的最简分数为 a ′ b ′ \dfrac{a'}{b'} b′a′,则 a ′ b ′ \dfrac{a'}{b'} b′a′的若干整数倍相当于将量筒等比例地放大,显然这并不影响结果的步数,因为目标是凑出特定的比例,并无数量上的要求.
(2)若 x y \dfrac{x}{y} yx不是最简分数,将其化为最简分数会使步数减小.
[证] 设 d = gcd ( x , y ) ≥ 2 d=\gcd(x,y)\geq 2 d=gcd(x,y)≥2, x y \dfrac{x}{y} yx的最简分数为 x ′ y ′ \dfrac{x'}{y'} y′x′.
x y \dfrac{x}{y} yx的答案 a n s = log a + b ( x + y ) + 1 = log a + b ( d x ′ + d y ′ ) + 1 = log a + b ( x ′ + y ′ ) + 1 + log a + b d ans=\log_{a+b}(x+y)+1=\log_{a+b}(dx'+dy')+1=\log_{a+b}(x'+y')+1+\log_{a+b}d ans=loga+b(x+y)+1=loga+b(dx′+dy′)+1=loga+b(x′+y′)+1+loga+bd.
x ′ y ′ \dfrac{x'}{y'} y′x′的答案 a n s ′ = log a + b ( x ′ + y ′ ) + 1 ans'=\log_{a+b}(x'+y')+1 ans′=loga+b(x′+y′)+1,则 a n s = a n s ′ + log a + b d ans=ans'+\log_{a+b}d ans=ans′+loga+bd.因 d ≥ 2 > 1 d\geq 2>1 d≥2>1,故 log a + b d > 0 \log_{a+b}d>0 loga+bd>0,故证.
代码 -> 2022CCPC湖北省赛-C(思维+构造)
void solve() {
ll x, y, a, b; cin >> x >> y >> a >> b;
ll d = gcd(x, y);
x /= d, y /= d; // 将x/y化为最简分数
d = gcd(a, b);
a /= d, b /= d; // 将a/b化为最简分数
ll ans = 0;
while (x && y) {
if (x > y) swap(x, y); // 保证x小
// cout << x << ' ' << y << endl; // 输出方案
if ((x + y) % (a + b)) {
cout << -1 << endl;
return;
}
ll k = (x + y) / (a + b);
if (x % a == 0) {
x = x / a;
y = k - x;
ans++;
}
else if (y % a == 0) {
x = y / a;
y = k - x;
ans++;
}
else {
cout << -1 << endl;
return;
}
}
cout << ans + 1 << endl;
}
int main() {
CaseT // 单测时注释掉该行
solve();
}
L. Chtholly and the Broken Chronograph
题意
维护一个长度为 n n n的序列 a 1 , ⋯ , a n a_1,\cdots,a_n a1,⋯,an,其中每个元素 a i a_i ai有一个状态 s i s_i si:① s i = 0 s_i=0 si=0表示第 i i i个元素禁用;② s i = 1 s_i=1 si=1表示第 i i i个元素启用.
现有如下四种操作:
① 1 x 1\ x 1 x,表示将 s x s_x sx置为 0 0 0,数据保证操作前 s x = 1 , 1 ≤ x ≤ n s_x=1,1\leq x\leq n sx=1,1≤x≤n
② 2 x 2\ x 2 x,表示将 s x s_x sx置为 1 1 1,数据保证操作前 s x = 0 , 1 ≤ x ≤ n s_x=0,1\leq x\leq n sx=0,1≤x≤n.
③ 3 l r x 3\ l\ r\ x 3 l r x,表示将区间 [ l , r ] [l,r] [l,r]中所有 s i = 1 s_i=1 si=1的 a i + = x a_i+=x ai+=x.数据保证 1 ≤ l ≤ r ≤ n , 1 ≤ x ≤ 1 e 8 1\leq l\leq r\leq n,1\leq x\leq 1\mathrm{e}8 1≤l≤r≤n,1≤x≤1e8.
④ 4 l r 4\ l\ r 4 l r,表示查询区间 [ l , r ] [l,r] [l,r]中所有 a i a_i ai之和,无论 a i a_i ai的状态.数据保证 1 ≤ l ≤ r ≤ n 1\leq l\leq r\leq n 1≤l≤r≤n.
第一行输入两个整数 n , q ( 1 ≤ n , q ≤ 1 e 5 ) n,q\ \ (1\leq n,q\leq 1\mathrm{e}5) n,q (1≤n,q≤1e5).第二行输入 n n n个整数 a 1 , ⋯ , a n ( 1 ≤ a i ≤ 1 e 8 ) a_1,\cdots,a_n\ \ (1\leq a_i\leq 1\mathrm{e}8) a1,⋯,an (1≤ai≤1e8).第三行输入 n n n个整数 s 1 , ⋯ , s n ( s i ∈ { 0 , 1 } ) s_1,\cdots,s_n\ \ (s_i\in\{0,1\}) s1,⋯,sn (si∈{0,1}).接下来 q q q行每行输入一个操作,格式如上.
思路
线段树节点维护一个变量 c n t cnt cnt表示区间内 s i = 1 s_i=1 si=1的 a i a_i ai的个数.
代码 -> 2022CCPC湖北省赛-L(线段树)
const int MAXN = 1e5 + 5;
namespace SegmentTree {
int n;
int a[MAXN];
int s[MAXN]; // 每个元素的状态
struct Node {
int l, r;
int s; // 元素的状态,s=0表示禁用,s=1表示启用
int cnt; // 区间s=1的元素个数
ll sum; // 区间和
ll lazy; // 加法懒标记
}SegT[MAXN << 2];
void push_up(int u) {
SegT[u].sum = SegT[u << 1].sum + SegT[u << 1 | 1].sum;
SegT[u].cnt = SegT[u << 1].cnt + SegT[u << 1 | 1].cnt;
}
void build(int u, int l, int r) {
SegT[u].l = l, SegT[u].r = r;
if (l == r) {
SegT[u].sum = a[l];
SegT[u].s = s[l];
SegT[u].cnt = SegT[u].s;
return;
}
int mid = l + r >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
push_up(u);
}
void push_down(int u) {
SegT[u << 1].sum += SegT[u].lazy * SegT[u << 1].cnt;
SegT[u << 1].lazy += SegT[u].lazy;
SegT[u << 1 | 1].sum += SegT[u].lazy * SegT[u << 1 | 1].cnt;
SegT[u << 1 | 1].lazy += SegT[u].lazy;
SegT[u].lazy = 0;
}
void modify_state(int u, int x) { // 反转a[x].s
if (SegT[u].l == SegT[u].r) { // 暴力修改叶子节点
SegT[u].s ^= 1;
SegT[u].cnt = SegT[u].s;
return;
}
push_down(u);
int mid = SegT[u].l + SegT[u].r >> 1;
if (x <= mid) modify_state(u << 1, x);
else modify_state(u << 1 | 1, x);
push_up(u);
}
void modify_add(int u, int l, int r, int x) {
if (l <= SegT[u].l && SegT[u].r <= r) {
SegT[u].sum += (ll)SegT[u].cnt * x;
SegT[u].lazy += x;
return;
}
push_down(u);
int mid = SegT[u].l + SegT[u].r >> 1;
if (l <= mid) modify_add(u << 1, l, r, x);
if (r > mid) modify_add(u << 1 | 1, l, r, x);
push_up(u);
}
ll query(int u, int l, int r) {
if (l <= SegT[u].l && SegT[u].r <= r) return SegT[u].sum;
push_down(u);
int mid = SegT[u].l + SegT[u].r >> 1;
ll res = 0;
if (l <= mid) res += query(u << 1, l, r);
if (r > mid) res += query(u << 1 | 1, l, r);
return res;
}
};
using namespace SegmentTree;
void solve() {
int q; cin >> n >> q;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= n; i++) cin >> s[i];
build(1, 1, n);
while (q--) {
int op; cin >> op;
if (op == 1 || op == 2) {
int x; cin >> x;
modify_state(1, x);
}
else if (op == 3) {
int l, r, x; cin >> l >> r >> x;
modify_add(1, l, r, x);
}
else {
int l, r; cin >> l >> r;
cout << query(1, l, r) << endl;
}
}
}
int main() {
solve();
}
F. Angel
题意
有编号 1 ∼ n 1\sim n 1∼n的 n n n个洞排成一行,兔子每次只能在一个洞中,且每个懂只能停留一秒.每一秒兔子会移动到相邻的洞,遇到边界时返回.每一秒兔子移动前,玩家可检查一个洞中是否有兔子,若有则抓到兔子.求一个最坏情况下能抓到兔子的所需时间最小的方案,或断言不能抓到兔子.
第一行输入一个整数 n ( 1 ≤ n ≤ 1000 ) n\ \ (1\leq n\leq 1000) n (1≤n≤1000).
若不能抓到兔子,输出 − 1 -1 −1;否则第一行输出所需的最小时间,第二行输出每一秒检查的洞的编号.
思路
兔子移动后奇偶性改变,假定其初始位置的奇偶性后,将其往一边赶,最坏情况只需正着赶一遍再倒着赶一遍.
不妨设 n > 2 n>2 n>2.注意到初始在奇数位置和在偶数位置的兔子不会跳到同一格子,且每一时刻奇偶性互换.注意到每次检查一个洞实际上是排除了某类奇偶性的一个可能,若两类奇偶性都存在且存在空位时,检查一类的奇偶性会使得另一类的奇偶性增加一个可能性,故需先排除一种奇偶性的全部可能.消除一类奇偶性最少需 ( n − 2 ) (n-2) (n−2)步,即从 2 , 3 , ⋯ , n − 1 2,3,\cdots,n-1 2,3,⋯,n−1,再将兔子倒着赶一遍,即 n − 1 , n − 2 , ⋯ , 2 n-1,n-2,\cdots,2 n−1,n−2,⋯,2,即可保证抓到兔子.
注意特判 n = 1 n=1 n=1和 n = 2 n=2 n=2的情况.
代码 -> 2022CCPC湖北省赛-F(思维)
void solve() {
int n; cin >> n;
if (n == 1) {
cout << "1\n1" << endl;
return;
}
else if (n == 2) {
cout << "2\n2 2" << endl;
return;
}
cout << 2 * (n - 2) << endl;
for (int i = 2; i <= n - 1; i++) cout << i << ' ';
for (int i = n - 1; i >= 2; i--) cout << i << ' ';
}
int main() {
solve();
}
A. Nucleic Acid Test
题意
给定一个包含 n n n个节点和 m m m条边的无向图,其中 k ( 1 ≤ k ≤ n ) k\ \ (1\leq k\leq n) k (1≤k≤n)个节点处有核酸点.选择一个核酸点出发,以速度 v v v遍历所有节点,并最后在核酸点结束,要求相邻两次核酸间隔不超过时间 t t t,求满足要求的最小速度(整数).
第一行输入三个整数 n , m , k ( 2 ≤ n ≤ 300 , 0 ≤ m ≤ n ( n − 1 ) 2 , 1 ≤ k ≤ n ) n,m,k\ \ \left(2\leq n\leq 300,0\leq m\leq \dfrac{n(n-1)}{2},1\leq k\leq n\right) n,m,k (2≤n≤300,0≤m≤2n(n−1),1≤k≤n).第二行输入一个整数 t ( 0 ≤ t ≤ 1 e 9 ) t\ \ (0\leq t\leq 1\mathrm{e}9) t (0≤t≤1e9).接下来 m m m行每行输入三个整数 a , b , c ( 1 ≤ a , b ≤ n , 1 ≤ c ≤ 1 e 9 ) a,b,c\ \ (1\leq a,b\leq n,1\leq c\leq 1\mathrm{e}9) a,b,c (1≤a,b≤n,1≤c≤1e9),表示节点 a a a与 b b b间存在长度为 c c c的无向边.数据保证无重边.最后一行输入 k k k个相异的整数 s 1 , ⋯ , s k s_1,\cdots,s_k s1,⋯,sk,表示 k k k个核酸点所在的节点编号.
若能从一个核算点出发,遍历所有节点,并最后在核酸点结束,输出最小速度(整数);否则输出 − 1 -1 −1.
思路I
n n n最大 300 300 300,显然可先用Floyd算法求出任意两点间的最短路.设非核酸点 x x x到核酸点 A A A和 B B B的距离分别为 d A d_A dA和 d B d_B dB,不妨设 d A > d B d_A>d_B dA>dB.若从 A A A出发经 x x x到 B B B,经过的路程为 d A + d B d_A+d_B dA+dB,造成的影响是 x x x被访问.注意到为访问 x x x,只需从 B B B出发,先走到 x x x,再返回 B B B,经过的路程为 2 d B < d A + d B 2d_B
注意 t = 0 t=0 t=0或图不连通时无解.
代码I -> 2022CCPC湖北省赛-A(Floyd+Kruskal)
const int MAXN = 305, MAXM = MAXN * MAXN;
int n, m, k; // 节点数、边数、核酸点数
int t; // 最大核酸间隔
int nucleic[MAXN]; // 核酸点编号
bool is_nucleic[MAXN]; // 记录每个节点是否是核酸点
namespace Floyd {
int n; // 节点数
ll d[MAXN][MAXN]; // d[u][v]表示节点u与v间的最短路
void init() { // 初始化d[][]
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) d[i][j] = i == j ? 0 : INFF;
}
void floyd() {
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
}
}
namespace Kruskal {
int n, m; // 节点数、边数
struct Edge {
int u, v;
ll w;
bool operator<(const Edge& B) { return w < B.w; }
}edges[MAXM];
int fa[MAXN]; // 并查集的fa[]数组
void init() { // 初始化fa[]
for (int i = 1; i <= n; i++) fa[i] = i;
}
int find(int x) { return x == fa[x] ? x : fa[x] = find(fa[x]); }
ll kruskal() { // 返回最小生成树的最长边,图不连通时返回INFF
sort(edges, edges + m); // 按边权升序排列
ll res = 0; // 最小生成树的最长边
int cnt = 0; // 当前连的边数
for (int i = 0; i < m; i++) {
auto [u, v, w] = edges[i];
u = find(u), v = find(v);
if (u != v) {
fa[u] = v;
res = max(res, w);
cnt++;
}
}
if (cnt < n - 1) return INFF; // 图不连通
else return res;
}
}
void build() { // 对核酸点建图
Kruskal::m = 0;
for (int i = 1; i <= k; i++) {
for (int j = i + 1; j <= k; j++)
Kruskal::edges[Kruskal::m++] = { nucleic[i],nucleic[j],Floyd::d[nucleic[i]][nucleic[j]] };
}
}
void solve() {
cin >> n >> m >> k >> t;
if (!t) {
cout << -1;
return;
}
Floyd::n = n;
Floyd::init();
while (m--) {
int a, b, c; cin >> a >> b >> c;
Floyd::d[a][b] = Floyd::d[b][a] = min(Floyd::d[a][b], (ll)c);
}
for (int i = 1; i <= k; i++) {
cin >> nucleic[i];
is_nucleic[nucleic[i]] = true;
}
Floyd::floyd();
ll maxlength = 0; // 每个节点到其最近的核酸点的最短距离的最大值
for (int i = 1; i <= n; i++) {
ll minlength = INFF; // 每个节点到其最近的核酸点的最短距离
if (is_nucleic[i]) { // 核酸点
for (int j = 1; j <= k; j++) {
if (nucleic[j] == i) continue;
minlength = min(minlength, Floyd::d[i][nucleic[j]]);
}
if (k == 1) minlength = 0; // 特判只有一个核酸点的情况
}
else { // 非核酸点
for (int j = 1; j <= k; j++) // 找到距该非核酸点最近的核酸点
minlength = min(minlength, Floyd::d[i][nucleic[j]] << 1);
}
maxlength = max(maxlength, minlength);
}
Kruskal::n = n;
Kruskal::init(); // 注意并查集要对n个节点都初始化
Kruskal::n = k; // 实际图中只有k个节点
build();
maxlength = max(maxlength, Kruskal::kruskal());
if (maxlength == INFF) cout << -1;
else cout << (maxlength + t - 1) / t;
}
int main() {
solve();
}
![]()
思路II
二分速度 v v v,每次只对距离不超过 v t vt vt的两节点连边,检查图的连通性即可.
代码II -> 2022CCPC湖北省赛-A(Floyd+并查集+二分)
const int MAXN = 305, MAXM = MAXN * MAXN;
int n, m, k; // 节点数、边数、核酸点数
int t; // 最大核酸间隔
bool is_nucleic[MAXN]; // 记录每个节点是否是核酸点
namespace Floyd {
int n; // 节点数
ll d[MAXN][MAXN]; // d[u][v]表示节点u与v间的最短路
void init() { // 初始化d[][]
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) d[i][j] = i == j ? 0 : INFF;
}
void floyd() {
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
}
}
namespace DSU {
int n; // 元素个数
int fa[MAXN]; // fa[]数组
int siz[MAXN]; // 集合大小
void init() { // 初始化fa[]、siz[]
for (int i = 1; i <= n; i++) fa[i] = i, siz[i] = 1;
}
int find(int x) { return x == fa[x] ? x : fa[x] = find(fa[x]); }
bool merge(int x, int y) { // 返回合并是否成功,即初始时是否不在同一集合中
x = find(x), y = find(y);
if (x != y) {
if (siz[x] > siz[y]) swap(x, y); // 保证x所在的集合小
fa[x] = y;
siz[y] += siz[x];
return true;
}
else return false;
}
}
bool vis[MAXN]; // 记录每个集合是否被遍历过
bool check(ll v) {
DSU::init();
for (int i = 1; i <= n; i++) vis[i] = false;
// 核酸点间连边
for (int i = 1; i <= n; i++) {
if (!is_nucleic[i]) continue;
for (int j = 1; j <= n; j++) {
if (!is_nucleic[j]) continue;
// if (v * t >= Floyd::d[i][j]) DSU::merge(i, j); // 注意此处乘法会爆ll
if ((double)Floyd::d[i][j] / v <= (double)t) DSU::merge(i, j);
}
}
// 非核酸点向核酸点连边
for (int i = 1; i <= n; i++) {
if (is_nucleic[i]) continue;
for (int j = 1; j <= n; j++) {
if (!is_nucleic[j]) continue;
// if (v * t >= 2 * Floyd::d[i][j]) DSU::merge(i, j); // 注意此处乘法会爆ll
if ((double)2 * Floyd::d[i][j] / v <= (double)t) DSU::merge(i, j);
}
}
int cnt = 0; // 连通块个数
for (int i = 1; i <= n; i++) {
int j = DSU::find(i);
if (!vis[j]) {
cnt++;
vis[j] = true;
if (cnt >= 2) return false; // 图不连通
}
}
return true;
}
void solve() {
cin >> n >> m >> k >> t;
if (!t) {
cout << -1;
return;
}
Floyd::n = n;
Floyd::init();
while (m--) {
int a, b, c; cin >> a >> b >> c;
Floyd::d[a][b] = Floyd::d[b][a] = min(Floyd::d[a][b], (ll)c);
}
for (int i = 1; i <= k; i++) {
int x; cin >> x;
is_nucleic[x] = true;
}
Floyd::floyd();
// 检查图的连通性
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (Floyd::d[i][j] >= INFF) { // 图不连通
cout << -1;
return;
}
}
}
DSU::n = n;
ll l = 1, r = 1e18; // 注意l最小取1
while (l < r) {
ll mid = l + r >> 1;
if (check(mid)) r = mid;
else l = mid + 1;
}
cout << l;
}
int main() {
solve();
}
J. Palindrome Reversion
题意
给定一个长度不超过 1 e 5 1\mathrm{e}5 1e5且只包含小写英文字母的字符串 s s s,下标从 1 1 1开始.问是否能翻转一个区间使得 s s s变为回文串,若能,输出翻转的区间;否则输出 − 1 − 1 -1\ -1 −1 −1.若有多组解,输出任一组.
思路
显然初始时 s s s首尾对称的部分不影响是否有解,可将其去掉.
观察样例,猜测若有解,则可通过翻转 s s s的前缀或后缀使其变为回文串.
有解的充要条件是:可通过翻转 s s s的前缀或后缀使其变为回文串.
[证] 如上图,用 s 1 s_1 s1的符号表示回文串.显然有解的情况如 s 2 s_2 s2和 s 3 s_3 s3所示.
分别翻转 s 2 s_2 s2和 s 3 s_3 s3的红色(后缀)、蓝色(前缀)部分即可将其变为回文串.
反之,通过翻转 s 1 s_1 s1的某一部分可将其变为有解的情况 s 2 s_2 s2或 s 3 s_3 s3.
代码 -> 2022CCPC湖北省赛-J(字符串哈希)
const int MAXN = 1e6 + 5;
struct StringHash {
int n; // 字符串长度
char str[MAXN]; // 下标从1开始
const ll Base1 = 29, MOD1 = 1e9 + 7;
const ll Base2 = 131, MOD2 = 1e9 + 9;
ll ha1[MAXN], ha2[MAXN]; // 正着的哈希值
ll rha1[MAXN], rha2[MAXN]; // 反着的哈希值
ll pow1[MAXN], pow2[MAXN]; // Base1和Base2的乘方
void init() { // 预处理pow1[]、pow2[]
pow1[0] = pow2[0] = 1;
for (int i = 1; i <= n; i++) {
pow1[i] = pow1[i - 1] * Base1 % MOD1;
pow2[i] = pow2[i - 1] * Base2 % MOD2;
}
}
void pre() { // 预处理ha1[]、ha2[]
for (int i = 1; i <= n; i++) {
ha1[i] = (ha1[i - 1] * Base1 + str[i]) % MOD1;
ha2[i] = (ha2[i - 1] * Base2 + str[i]) % MOD2;
rha1[i] = (rha1[i - 1] * Base1 + str[n - i + 1]) % MOD1;
rha2[i] = (rha2[i - 1] * Base2 + str[n - i + 1]) % MOD2;
}
}
pll get_hash(int l, int r) { // 求子串str[l...r]正着的哈希值
ll res1 = ((ha1[r] - ha1[l - 1] * pow1[r - l + 1]) % MOD1 + MOD1) % MOD1;
ll res2 = ((ha2[r] - ha2[l - 1] * pow2[r - l + 1]) % MOD2 + MOD2) % MOD2;
return pll(res1, res2);
}
pll get_rhash(int l, int r) { // 求子串str[l...r]反着的哈希值
ll res1 = ((rha1[n - l + 1] - rha1[n - r] * pow1[r - l + 1]) % MOD1 + MOD1) % MOD1;
ll res2 = ((rha2[n - l + 1] - rha2[n - r] * pow2[r - l + 1]) % MOD2 + MOD2) % MOD2;
return pll(res1, res2);
}
bool IsPalindrome(int l, int r) { // 判断子串str[l...r]是否是回文串
return get_hash(l, r) == get_rhash(l, r);
}
pll add(pll a, pll b) {
ll res1 = (a.first + b.first) % MOD1;
ll res2 = (a.second + b.second) % MOD2;
return pll(res1, res2);
}
pll mul(pll& a, ll k) { // a *= Base的k次方
ll res1 = a.first * pow1[k] % MOD1;
ll res2 = a.second * pow2[k] % MOD2;
return pll(res1, res2);
}
}solver;
void solve() {
cin >> solver.str + 1;
solver.n = strlen(solver.str + 1);
solver.init();
solver.pre();
int l = 1, r = solver.n;
while (l < r && solver.str[l] == solver.str[r]) l++, r--; // 去掉两边相同的字符
if (l >= r) { // 原串是回文串
cout << "1 1" << endl;
return;
}
for (int i = l; i <= r; i++) { // 翻转前缀str[l...i]
auto tmp1 = solver.get_rhash(l, i), tmp2 = solver.get_hash(i + 1, r);
auto res1 = solver.add(solver.mul(tmp1, r - i), tmp2);
auto tmp3 = solver.get_hash(l, i), tmp4 = solver.get_rhash(i + 1, r);
auto res2 = solver.add(solver.mul(tmp4, i - l + 1), tmp3);
if (res1 == res2) {
cout << l << ' ' << i;
return;
}
}
for (int i = l; i <= r; i++) { // 反转后缀str[i...r]
auto tmp1 = solver.get_hash(l, i - 1), tmp2 = solver.get_rhash(i, r);
auto res1 = solver.add(solver.mul(tmp1, r - i + 1), tmp2);
auto tmp3 = solver.get_rhash(l, i - 1), tmp4 = solver.get_hash(i, r);
auto res2 = solver.add(solver.mul(tmp4, i - l), tmp3);
if (res1 == res2) {
cout << i << ' ' << r;
return;
}
}
cout << "-1 -1";
}
int main() {
solve();
}