最优贸易（codevs 1173）题解

【问题描述】

C 国有n 个大城市和m 条道路，每条道路连接这n 个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这m 条道路中有一部分为单向通行的道路，一部分为双向通行的道路，双向通行的道路在统计条数时也计为1 条。C 国幅员辽阔，各地的资源分布情况各不相同，这就导致了同一种商品在不同城市的价格不一定相同。但是，同一种商品在同一个城市的买入价和卖出价始终是相同的。商人阿龙来到 C 国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息之后，便决定在旅游的同时，利用商品在不同城市中的差价赚回一点旅费。设C 国n 个城市的标号从1~ n，阿龙决定从1 号城市出发，并最终在n 号城市结束自己的旅行。在旅游的过程中，任何城市可以重复经过多次，但不要求经过所有n 个城市。阿龙通过这样的贸易方式赚取旅费：他会选择一个经过的城市买入他最喜欢的商品——水晶球，并在之后经过的另一个城市卖出这个水晶球，用赚取的差价当做旅费。由于阿龙主要是来C 国旅游，他决定这个贸易只进行最多一次，当然，在赚不到差价的情况下他就无需进行贸易。假设 C 国有5 个大城市，城市的编号和道路连接情况如下图，单向箭头表示这条道路为单向通行，双向箭头表示这条道路为双向通行。

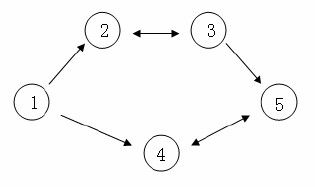
假设 1~n 号城市的水晶球价格分别为4，3，5，6，1。阿龙可以选择如下一条线路：1->2->3->5，并在2 号城市以3 的价格买入水晶球，在3号城市以5 的价格卖出水晶球，赚取的旅费数为2。阿龙也可以选择如下一条线路 1->4->5->4->5，并在第1 次到达5 号城市时以1 的价格买入水晶球，在第2 次到达4 号城市时以6 的价格卖出水晶球，赚取的旅费数为5。

现在给出 n 个城市的水晶球价格，m 条道路的信息（每条道路所连接的两个城市的编号以及该条道路的通行情况）。请你告诉阿龙，他最多能赚取多少旅费。

【样例输入】

    5 5
    4 3 5 6 1
    1 2 1
    1 4 1
    2 3 2
    3 5 1
    4 5 2

【样例输出】

    5

【解题思路】

本题为NOIP2009第三题，主要思想还是求最短路径，只不过这道题数据范围过大，我们需要用邻接表存储数据。实际上这里我们求最短路径是求最小价格和最大价格，我们需要求两遍最短路径，一遍求从1到该城市路经的水晶球的最小价格，另一遍求该城市到n路经的水晶球的最大价格，然后把每一个城市搜一遍，比较最小值和最大值即可。

那么，我们就可以想到用两个邻接表，一个正着存边，一个倒着存边。那么在求最短路径的时候需要注意，应该是当前的路径上记录下来的最小价格（最大价格）与扩展的城市的价格之间更小（大）的一个数比记录下来的小（大）就需要扩展，详见代码。

【代码实现】

  1 uses math;

  2 type rec=record

  3      c,next:longint;

  4 end;

  5 var e,e1:array[1..500000] of rec;

  6     g,g1:array[1..100000] of rec;

  7     n,m,efree,i,a,b,c,ans,efree1:longint;

  8     f:array[1..100000] of boolean;

  9     d1,dn,s:array[1..100000] of longint;

 10 procedure ins(y:longint;var p:rec);

 11 begin

 12  e[efree].c:=y;

 13  e[efree].next:=p.next;

 14  p.next:=efree;

 15  inc(efree);

 16 end;

 17 procedure ins1(y:longint;var p:rec);

 18 begin

 19  e1[efree1].c:=y;

 20  e1[efree1].next:=p.next;

 21  p.next:=efree1;

 22  inc(efree1);

 23 end;

 24 procedure spfa;

 25 var i,v,u,h,t:longint;

 26     q:array[1..100000] of longint;

 27 begin

 28  d1[1]:=s[1];

 29  f[1]:=true;

 30  h:=0;

 31  t:=1;

 32  q[1]:=1;

 33  while h<>t do

 34   begin

 35    h:=(h mod 100000)+1;

 36    v:=q[h];

 37    f[v]:=false;

 38    i:=g[v].next;

 39    while i<>-1 do

 40     begin

 41      u:=e[i].c;

 42      if min(d1[v],s[u])<d1[u] then

 43       begin

 44        d1[u]:=min(s[u],d1[v]);

 45        if not f[u] then

 46         begin

 47          f[u]:=true;

 48          t:=(t mod 100000)+1;

 49          q[t]:=u;

 50         end;

 51       end;

 52      i:=e[i].next;

 53     end;

 54   end;

 55 end;

 56 procedure spfa1;

 57 var i,v,u,h,t:longint;

 58     q:array[1..100000] of longint;

 59 begin

 60  dn[n]:=s[n];

 61  f[n]:=true;

 62  h:=0;

 63  t:=1;

 64  q[1]:=n;

 65  while h<>t do

 66   begin

 67    h:=(h mod 100000)+1;

 68    v:=q[h];

 69    f[v]:=false;

 70    i:=g1[v].next;

 71    while i<>-1 do

 72     begin

 73      u:=e1[i].c;

 74      if max(dn[v],s[u])>dn[u] then

 75       begin

 76        dn[u]:=max(dn[v],s[u]);

 77        if not f[u] then

 78         begin

 79          f[u]:=true;

 80          t:=(t mod 100000)+1;

 81          q[t]:=u;

 82         end;

 83       end;

 84      i:=e1[i].next;

 85     end;

 86   end;

 87 end;

 88 begin

 89  readln(n,m);

 90  for i:=1 to n do

 91   begin

 92    g[i].next:=-1;

 93    g1[i].next:=-1;

 94   end;

 95  efree:=1;

 96  efree1:=1;

 97  for i:=1 to n do

 98   begin

 99    read(s[i]);

100    d1[i]:=maxlongint;

101   end;

102  for i:=1 to m do

103   begin

104    readln(a,b,c);

105    case c of

106     1:

107      begin

108       ins(b,g[a]);

109       ins1(a,g1[b]);

110      end;

111     2:

112      begin

113       ins(b,g[a]);

114       ins(a,g[b]);

115       ins1(a,g1[b]);

116       ins1(b,g1[a]);

117      end;

118    end;

119   end;//两个邻接表，注意单向路和双向路

120  spfa;

121  fillchar(f,sizeof(f),false);

122  spfa1;

123  for i:=1 to n do

124   if dn[i]-d1[i]>ans then

125    ans:=dn[i]-d1[i];

126  writeln(ans);

127 end.