0.1 + 0.2 为什么不等于 0.3之小数精度问题

浮点数精度丢失，一直是前端面试八股文里很常见的一个问题，今天我们就来深入的了解一下问题背后的原理，以及给一些日常处理的小技巧。

问题

1、0.1 + 0.2 ≠ 0.3反而 0.1+0.2 = 0.30000000000000004

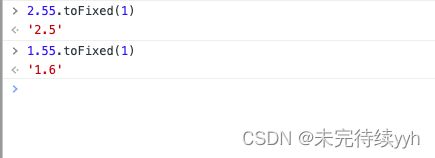
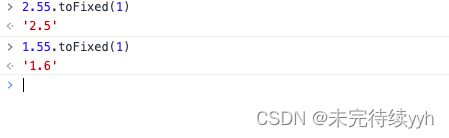
2、2.55.toFixed(1) = 2.5， 而 1.55.toFixed(1) = 1.6

其实以上都是因为浮点数精度问题导致的

原因

我们在计算数学问题的时候，使用的是十进制，计算0.1 + 0.2的结果等于0.3，没有任何问题。但在计算机中，存储数据使用的是二进制，数据由0和1组成。所以在对数据进行计算时，需要将数据全部转换成二进制，再进行数据计算。

• 在base10 （十进制）的系统（由人类使用）中，如果使用以10为底的质因数，则可以精确表示分数。
• 在base 2 （二进制）的系统中（由计算机使用），如果使用以 2为底的素因子，则可以精确表示分数

进制转换：

十进制转二进制的主要原则如下所示：

• 十进制整数转换为二进制整数：除2取余，逆序排列
• 十进制小数转换为二进制小数：乘2取整，顺序排列
  这里主要介绍小数转换。十进制小数转二进制，小数部分，乘 2 取整数，若乘之后的小数部分不为 0，继续乘以 2 直到小数部分为 0 ，将取出的整数正向排序。

正整数的转换方法：

除二取余，然后倒序排列，高位补零
例如： 65 转二进制

65 转二进制为 1000001，高位 0 后为 01000001

小数的转换方法：

对小数点以后的数乘以 2，取整数部分，再取小数部分乘 2，以此类推…… 直到小数部分为 0 或位数足够。取整部分按先后顺序排列即可

例如： 0.1 转二进制

0.1 * 2 = 0.2 --------------- 取整数 0，小数 0.2
0.2 * 2 = 0.4 --------------- 取整数 0，小数 0.4
0.4 * 2 = 0.8 --------------- 取整数 0，小数 0.8
0.8 * 2 = 1.6 --------------- 取整数 1，小数 0.6
0.6 * 2 = 1.2 --------------- 取整数 1，小数 0.2
0.2 * 2 = 0.4 --------------- 取整数 0，小数 0.4
0.4 * 2 = 0.8 --------------- 取整数 0，小数 0.8
0.8 * 2 = 1.6 --------------- 取整数 1，小数 0.6
0.6 * 2 = 1.2 --------------- 取整数 1，小数 0.2
...

最终 0.1 的二进制表示为 0.000110011… 后面将会 0011 无限循环，因此二进制无法精确的保存类似 0.1 这样的小数。十进制小数转二进制后大概率出现无限位数！但计算机存储是有限，那这样无限循环也不是办法，又该保存多少位呢？也就有了我们接下来要重点讲解的 IEEE 754 标准。

IEEE 754

维基百科链接 的链接，感兴趣的自行了解一下。

这里用一句话概述，IEEE754是一种二进制浮点数算术标准。

IEEE 754 常用的两种浮点数值的表示方式为：单精确度（32位）、双精确度（64位）。例如， java语言中的 float 通常是指 IEEE 单精确度，而 double 是指双精确度。

在 JavaScript 中不论小数还是整数只有一种数据类型表示，这就是 Number 类型，其遵循 IEEE 754 标准，使用双精度浮点数（double）64 位（8 字节）来存储一个浮点数。

溯源：浮点型存储机制

浮点型数据类型主要有：单精度（float）、双精度（double）

单精度浮点数（float）

在内存中占 4 个字节、有效数字 8 位、表示范围：-3.40E+38 ~ +3.40E+38

双精度浮点数（double）

在内存中占 8 个字节、有效数字 16 位、表示范围：-1.79E+308 ~ +1.79E+308

• sign bit（S，符号）：用来表示正负号，0 为 正 1 为 负（1 bit）
• exponent（E，指数）：用来表示次方数（11 bits）
• Significand（M，尾数）：用来表示精确度 1 <= M < 2（52 bits）

在这个标准下，我们会用 1 位存储 S(sign)，0 表示正数，1 表示负数。用 11 位存储 E(exponent) + bias，对于 11 位来说，bias 的值是 2^(11-1) - 1，也就是 1023。用 52 位存储 Fraction。

举个例子，就拿 0.1 来看，对应二进制是 1 * 1.1001100110011…… * 2^-4， Sign 是 0，E + bias 是 -4 + 1023 = 1019，1019 用二进制表示是 1111111011，Fraction 是 1001100110011……

0.1 用64为表示

0 01111111011 1001100110011001100110011001100110011001100110011010

0.2 用64为表示

0 01111111100 1001100110011001100110011001100110011001100110011010

可以看出来在转换为二进制时

0.1 >>> 0.0001 1001 1001 1001...（1001无限循环）
0.2 >>> 0.0011 0011 0011 0011...（0011无限循环）

将 0.1 和 0.2 的二进制形式按实际展开，末尾补零相加，结果如下：

 0.00011001100110011001100110011001100110011001100110011010
+0.00110011001100110011001100110011001100110011001100110100
=0.01001100110011001100110011001100110011001100110011001110

用科学计数法表示为：

1.001100110011001100110011001100110011001100110011010 * 2^(-2)

因此 0.1 + 0.2

0 01111111101 0011001100110011001100110011001100110011001100110100

再转十进制为：0.30000000000000004

小结：计算机存储双进度浮点数，需要先把十进制转换为二进制的科学计数法形式，然后计算机以一定的规则（IEEE 754）存储，因为存储时有位数限制（双进度 8 字节，64 位），末位就需要取近似值（0 舍 1 入），再转换为十进制时，就造成了误差。

解决方法：

转换为整数计算

function add(num1, num2) {
    //num1 小数位的长度
 const num1Digits = (num1.toString().split('.')[1] || '').length;
 //num2 小数位的长度
 const num2Digits = (num2.toString().split('.')[1] || '').length;
 // 取最大的小数位作为10的指数
 const baseNum = Math.pow(10, Math.max(num1Digits, num2Digits));
 // 把小数都转为整数然后再计算
 return (num1 * baseNum + num2 * baseNum) / baseNum;
}

把计算数字 提升 10 的N次方 倍 再 除以 10的N次方。N>1

使用ES6提供的极小数Number.EPSILON：

function numbersequal(a,b){ 
    return Math.abs(a-b) < Number.EPSILON;
} 
var a=0.1+0.2， b=0.3;
console.log(numbersequal(a,b)); //true

类库

1、math.js

math.js是JavaScript和Node.js的一个广泛的数学库。支持数字，大数，复数，分数，单位和矩阵等数据类型的运算。

官网：http://mathjs.org/

GitHub：https://github.com/josdejong/mathjs

0.1+0.2 ===0.3实现代码：
var math = require('mathjs')
console.log(math.add(0.1,0.2))//0.30000000000000004
console.log(math.format((math.add(math.bignumber(0.1),math.bignumber(0.2)))))//'0.3'

2、decimal.js

为 JavaScript 提供十进制类型的任意精度数值。

官网：http://mikemcl.github.io/decimal.js/

GitHub：https://github.com/MikeMcl/decimal.js

var Decimal = require('decimal.js')
x = new  Decimal(0.1)
y = 0.2
console.log(x.plus(y).toString())//'0.3'

3、bignumber.js

用于任意精度算术的JavaScript库。

官网：[http://mikemcl.github.io/bignumber.js/]（http://mikemcl.github.io/bignumber.js/）

Github：https://github.com/MikeMcl/bignumber.js

var BigNumber = require("bignumber.js")
x = new BigNumber(0.1)
y = 0.2
console.log(x.plus(y).toString())//'0.3'

4、big.js

用于任意精度十进制算术的小型快速JavaScript库。

官网：http://mikemcl.github.io/big.js/

Github：https://github.com/MikeMcl/big.js/

var Big = require("big.js")
x = new Big(0.1)
y = 0.2
console.log(x.plus(y).toString())//'0.3'

类似问题

javascript中toFixed使用的是银行家舍入规则。

据说大部分的编程软件都使用的是这种方法，也算是一种国际标准。所谓银行家舍入法，其实质是一种四舍六入五取偶（又称四舍六入五留双）法。其规则是：当舍去位的数值小于5时，直接舍去该位；当舍去位的数值大于等于6时，在舍去该位的同时向前位进一；当舍去位的数值等于5时，如果前位数值为奇，则在舍去该位的同时向前位进一，如果前位数值为偶，则直接舍去该位。

网上给了一种通用的解法，在四舍五入前，给数字加一个极小值，比如 1e-14：

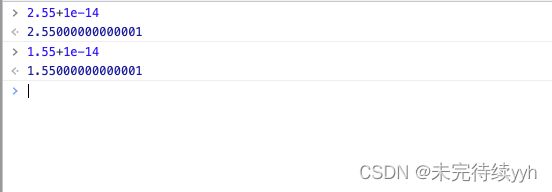
这样处理后，大部分场景下的精度基本都够用了。

这里我们采用的极小值是 10 的负 14 次方（1e-14），有没有一个官方推荐的极小值常量呢？嘿，巧了，还真有！ES6 在 Number 对象上新增了一个极小的常量 Number.EPSILON：

 Number.EPSILON
 // 2.220446049250313e-16
 Number.EPSILON.toFixed(20)
 // "0.00000000000000022204"

引入一个这么小的量，目的在于为浮点数计算设置一个误差范围，如果误差能够小于 Number.EPSILON，我们就可以认为结果是可靠的。

解法总结

• 浮点数计算类，取二者中小数位数最长者（记为 N），同时乘以 10 的 N 次幂，转换为整数进行计算，再除以 N 次幂转回小数
• 需要用 toFixed 取近似值的地方，可以先加上 1e-14 或 umber.EPSILON，再取。
• 判定两个数字相等，可以使用 Math.abs(left - right) < Number.EPSILON
• 实在不会，就直接用别人写好的成熟库吧。

参考链接：
https://www.jianshu.com/p/f5e106affd96