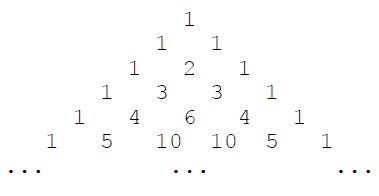2021年第十二届蓝桥杯javaB组题解

前五题为选择题，后面五题为大题

​​​​​​A题:ASC【5分】

【题目描述】

已知大写字母 A 的 ASCII 码为 65，请问大写字母 L 的 ASCII 码是多少？

【答案】：76

【题解】简单的acsll计算，按照字母表，A为第1个，L为第12个，故L的ASCll码为65+11=76.

B题：卡片【5分】

【题目描述】

小蓝有很多数字卡片，每张卡片上都是数字0 到9。
小蓝准备用这些卡片来拼一些数，他想从1 开始拼出正整数，每拼一个，就保存起来，卡片就不能用来拼其它数了。
小蓝想知道自己能从1 拼到多少。
例如，当小蓝有30 张卡片，其中0 到9 各3 张，则小蓝可以拼出1 到10，但是拼11 时卡片1 已经只有一张了，不够拼出11。
现在小蓝手里有0 到9 的卡片各2021 张，共20210 张，请问小蓝可以从1拼到多少？
提示：建议使用计算机编程解决问题。

【答案】：3181

【题解】：0-9的卡片每个数字有2021张，从1开始遍历，每遍历到一个数字，这个卡片数字的个数就-1，如果某一个数字的卡片没有了，就遍历结束了。

import java.util.Arrays;

public class Main {
	static int a[] = new int[10];//0-9
	public static void main(String[] args) {
		Arrays.fill(a, 2021);//每个数初始值为2021
		int ans = 0;
		for(int i = 1; i <= 20210; i++) {
			int t = i;
			while(t > 0) {
				int s = t % 10;
				t /= 10;
				a[s]--;
				//注意：这里不是==0，上面a[s]--,减了一次才为0，说明这次没减之前为1，还有最后一个数，
				//如果为0，-1就会小于0，说明这个数2021张牌都用完啦
				
				if(a[s] < 0) {
					ans = i-1; //当前遍历的这个数肯定没有遍历完，故遍历到这个数的前一个
					break;
				}
			}
			if(ans != 0)	break;
		}
		System.out.println(ans);
	}
}

C题：直线【10分】

【题目描述】

在平面直角坐标系中，两点可以确定一条直线。
如果有多点在一条直线上，那么这些点中任意两点确定的直线是同一条。
给定平面上2 × 3 个整点{(x, y)|0 ≤ x < 2, 0 ≤ y < 3, x ∈ Z, y ∈ Z}，
即横坐标是0 到1 (包含0 和1) 之间的整数、纵坐标是0 到2 (包含0 和2) 之间的整数的点。
这些点一共确定了11 条不同的直线。
给定平面上20 × 21 个整点{(x, y)|0 ≤ x < 20, 0 ≤ y < 21, x ∈ Z, y ∈ Z}，
即横坐标是0 到19 (包含0 和19) 之间的整数、纵坐标是0 到20 (包含0 和20) 之间的整数的点。
请问这些点一共确定了多少条不同的直线。

【答案】：40257

【题解】这题的做法是先保存所有直线的斜率k和截距b，然后去重就可以得到结果。

其中最重要的是找到每一条直线的k和b(y=kx+b)，然后要去重，因为每一条直线上可能有多个节点，遍历的时候会重复，然后在记录k和b的时候最好不要使用double,因为精度不好控制,我使用的是String储存。当直线为x=b的时候没有斜率，在题中一共有20条，在最后加上即可。

import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;


public class Main{
	static ListsList = new ArrayList<>();
	
	static int gcd(int a,int b) {
		return b != 0 ? gcd(b, a % b) : a;
	}
	public static void main(String[] args) {
		for(int x1 = 0; x1 < 20; x1++) {
			for(int y1 = 0; y1 < 21; y1++) {
				for(int x2 = 0; x2 < 20; x2++) {
					for(int y2 = 0; y2 < 21; y2++) {
						if(x1 != x2) {
							String line = "";//存储k和b
							int y = y2 - y1;
							int x = x2 - x1;
							int g = gcd(y,x);//求两个数的最小公倍数,记录最简分数(唯一）
							line =  y / g + "/" + x / g;//k = (y2 - y1) / (x2 - x1);
							
							int b = y1 * x - x1 * y;//b =( y * (x2 - x1) - x * (y2 - y1)) / (x2 - x1)
							int g1 = gcd(b, x);
							line = line +"&"+ b / g1 + "/" + x / g1;
							sList.add(line);
						}
					}
				}
			}
		}
		
		long ans = 0L;
		Mapmap = new HashMap<>();
		for(int i = 0; i < sList.size(); i++) {
			if(!map.containsKey(sList.get(i))) {
				ans++;
//				System.out.println(sList.get(i));
				map.put(sList.get(i), true);
			}
		}
		System.out.println(ans+20);
	
	}	
}

D题：货物摆放【10分】

【题目描述】

小蓝有一个超大的仓库，可以摆放很多货物。
现在，小蓝有n 箱货物要摆放在仓库，每箱货物都是规则的正方体。
小蓝规定了长、宽、高三个互相垂直的方向，每箱货物的边都必须严格平行于长、宽、高。
小蓝希望所有的货物最终摆成一个大的立方体。即在长、宽、高的方向上分别堆L、W、H 的货物，满足n = L × W × H。
给定n，请问有多少种堆放货物的方案满足要求。
例如，当n = 4 时，有以下6 种方案：1×1×4、1×2×2、1×4×1、2×1×2、2×2×1、4×1×1。
请问，当n = 2021041820210418 （注意有16 位数字）时，总共有多少种
方案？
提示：建议使用计算机编程解决问题。

【答案】：2430

【题解】这一题是问我们有n箱货物可以有多少种摆放方法，通过案例可以得知L，W，H，都是n的质因子（L* W*H=n)，因此我们可以记录n的所以质因子，然后通过双重循环可以确定两个未知数，另外已知n,可以求出另一个未知数(H = n / (L * w))，题中要求算出一共多少种，所以只要满足条件（n % (L * W)) == 0即可。

import java.util.LinkedList;
import java.util.List;

public class Main {
	static Listlist = new LinkedList<>();
	
	public static void main(String[] args) {
		long n = 2021041820210418L;
		for(long i = 1; i <= n / i; i++) {//算出n的所有质因数
			if(n % i == 0) {
				list.add(i);
				if(i != n / i) {
					list.add(n / i);
				}
			}
		}
		long ans = 0L;
		for(long a : list) {//双重循环找答案
			for(long b : list) {
				if(n % (a * b) == 0)	ans++;
			}
		}
		System.out.println(ans);
	}
}

E题：路径【15分】

【题目描述】

小蓝学习了最短路径之后特别高兴，他定义了一个特别的图，希望找到图中的最短路径。
小蓝的图由2021 个结点组成，依次编号1 至2021。
对于两个不同的结点a, b，如果a 和b 的差的绝对值大于21，则两个结点之间没有边相连；
如果a 和b 的差的绝对值小于等于21，则两个点之间有一条长度为a 和b 的最小公倍数的无向边相连。
例如：结点1 和结点23 之间没有边相连；结点3 和结点24 之间有一条无向边，长度为24；
结点15 和结点25 之间有一条无向边，长度为75。
请计算，结点1 和结点2021 之间的最短路径长度是多少。
提示：建议使用计算机编程解决问题。

【答案】：10266837

【题解】这个题是最短路径的板子题，因为a和b 的绝对值不能大于21，说明a最多需要和42个点求最小公倍数来建无向边。求最短路径我用的是Dijkstra。

import java.util.Arrays;

public class Main {
	static int N = 2050,n = 2021,INF = 0x3f3f3f3f;
	static int g[][] = new int[N][N];
	static int dist[] = new int[N];
	static boolean st[] = new boolean[N];
	
	static int gcd(int a,int b) {
		return b != 0 ? gcd(b, a % b) : a;
	}
	
	static int dijkstra() {
		Arrays.fill(dist, INF);
		dist[1] = 0;
		for(int i = 1; i < n; i++) {
			int t = -1;
			for(int j = 1; j <= n; j++) {
				if(!st[j] && (t== -1 || dist[t] > dist[j] + g[t][j])) {
					t = j;
				}
			}
			st[t] = true;
			for(int j = 1; j <= n; j++) {
				dist[j] = Math.min(dist[j], dist[t] + g[t][j]);
			}
		}
		return dist[n];
	}
	public static void main(String[] args) {
		for(int i = 1; i < N; i++) {
			Arrays.fill(g[i], INF);
		}
		for(int i = 1; i <= n; i++) {
			for(int j = Math.max(1, i - 21); j <= Math.min(2021, i + 21); j++) {
				int t = gcd(i, j);
				g[i][j] = g[j][i] = (i * j) / t;
			}
		}
		System.out.println(dijkstra());
	}
}

F题：时间显示【15分】

【题目描述】

小蓝要和朋友合作开发一个时间显示的网站。
在服务器上，朋友已经获取了当前的时间，用一个整数表示。
值为从1970 年1 月1 日00:00:00 到当前时刻经过的毫秒数。
现在，小蓝要在客户端显示出这个时间。
小蓝不用显示出年月日，只需要显示出时分秒即可，毫秒也不用显示，直接舍去即可。
给定一个用整数表示的时间，请将这个时间对应的时分秒输出。

【输入格式】
输入一行包含一个整数，表示时间。

【输出格式】
输出时分秒表示的当前时间，格式形如 HH:MM:SS，其中 HH 表示时，值 为 0 到 23，MM 表示分，值为 0 到 59，SS 表示秒，值为 0 到 59。时、分、秒 不足两位时补前导 0。

【样例输入 1】
46800999

【样例输出 1】
13:00:00

【样例输入 2】
1618708103123

【样例输出 2】
01:08:23

【测评用例规模与约定】

对于所有评测用例，给定的时间为不超过 10的18次方的正整数。

【题解】题目是给出毫秒数，然后只需要显示时、分、秒，说明答案是在24小时之内。首先可以将输入的时间模除以一天的时间，将时间控制在24小时之内。然后分别算出时、分、秒即可。

一天：24 x 60 x 60 x 1000 (小时 x 分钟 x 秒 x 毫秒）= 86,400,000(毫秒）

以实例2为例子 1618708103123 % 86,400,000 = 4,103,123；

从毫秒转入秒：4,103,123 / 1000 = 4103（秒）

时： 4103 /（60 * 60） =  1（时）；

剩余秒数：4103 %（60 * 60）= 503；

分：503 / 60 = 8（分）；

剩余秒数：503 % 60 = 23（秒）

答案：01：08：23

java的补前导0可以使用printf输出。

import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
	    long n = sc.nextLong();
		n = n % (24 * 60 * 60 * 1000);
		n /= 1000;
		int h = (int) (n / 3600) ;
		int m = (int) ((n % 3600) / 60);
		int s = (int) ((n % 3600) % 60);
		System.out.printf("%02d:%02d:%02d\n",h,m,s);
		sc.close();
	}
}

G题：最少砝码【20分】

【题目描述】

你有一架天平。现在你要设计一套砝码，使得利用这些砝码可以称出任意小于等于N的正整数重量。
那么这套砝码最少需要包含多少个砝码？
注意砝码可以放在天平两边。

【输入格式】

一行包含一个正整数N。

【输出格式】

一行输出一个表示答案。

【输入样例】

7

【输出样例】

3

【样例说明】

33 个砝码重量是 1、4、6，可以称出 1 至 7的所有重量。

1 = 1;

2 = 6 − 4(天平一边放 66，另一边放 44)；

3 = 4 − 1;

4 = 4；

5 = 6 − 1；

6 = 6；

7 = 1 + 6；

少于 3 个砝码不可能称出 1 至 7 的所有重量。

【测评用例规模与约定】

对于所有评测用例，1 ≤ N ≤ 1000000000。

【题解】可以一步一步推过来，一个砝码的时候先加一个1，如果第二个砝码是2，那么最远可以拼到3（1，2，1+2），而如果第二个砝码是3的话，最远可以拼接到4（1，3-1，3，3+1）减法代表放在天平两边，加法代表放在天平的同一边。如果第二个砝码是4的话，不能拼到数字2（1，2=？，4-1=3，4，4+1=5），所以要拼到更大的数需要第三个砝码，以此类推，我发现当第三个砝码为9时达到最大数字13（1，3-1，3，3+1，9-3-1，9-3，9+1-3，9-1，9，9+1，9+3-1，9+3，9+3+1）；因此得到规律：

选择的砝码	最大的数量
1	1
3	4
9	13
...	...

import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		int ans = 0;
		while(n > 0) {
			n = n - (int)Math.pow(3, ans);
			ans++;
		}
		System.out.println(ans);
		sc.close();
	}
}

H题：杨辉三角【20分】

【题目描述】

下面的图形是著名的杨辉三角形：

 

如果我们按从上到下、从左到右的顺序把所有数排成一列，可以得到如下数列：
1, 1, 1, 1, 2, 1, 1, 3, 3, 1, 1, 4, 6, 4, 1, ...
给定一个正整数N，请你输出数列中第一次出现N 是在第几个数？

【输入格式】
输入一个整数N。

【输出格式】

对于每组测试数据输出一行表示答案。

【输入样例】

6

【输出样例】

13

【测评用例规模与约定】

对于 20% 的评测用例，1≤N≤10；

对于所有评测用例，1≤N≤1000000000。

【题解】我直接打暴力骗分。。。

还有两个大题不会写，听大佬说只要前面7个题都对，最后三个打暴力骗点分就可以拿到省一了，，，呀呀呀，大家都太强了，我好菜......