运放补偿网络波特图LTspice仿真：PI、II型、PID

运放补偿网络波特图LTspice仿真：PI、II型、PID

偏置调节电路

补偿器的输出电压只有在一定的范围内时才能正常工作。开环工作时，补偿器的输出很容易饱和，导致仿真结果不正确。
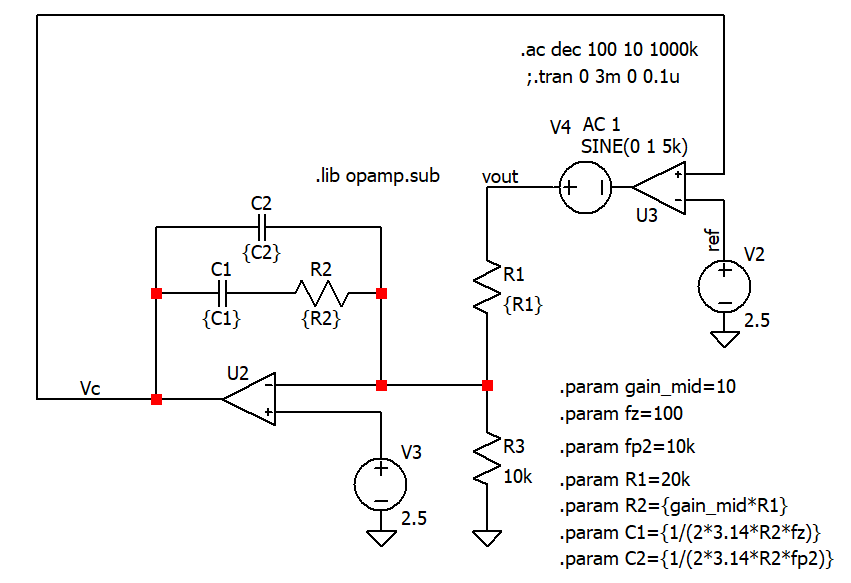
所以，需要加一个偏置调节电路，使得补偿器的输出电压Vc在合适范围内，如下图，参考LDO的原理，搭建了一个偏置调节电路。

• 补偿器输出Vc直连理想运放U3的正输入，电压源V2设置Vc的电压为3V
• 理想运放U3的输出为vout
• vout经过分压网络后，连接到补偿器的输入。

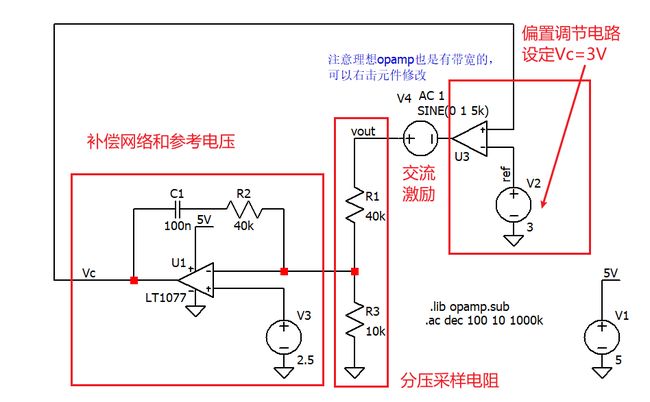
偏置调节的原理： Vc>3V——U3的输出Vout↑——补偿器输入↑——补偿器输出Vc↓。

然后在这个环路中加入一个交流激励V4，就可以通过ac仿真来获得补偿器的波特图。对于上图，控制器的传递函数为：$G_c(s)=\frac{V_c(s)}{V_{out}(s)}$
绘制波特图时公式相同（但是，一般看补偿器的波特图时，不考虑引入的180°相位，所以最终公式为 -Vc/Vout）。

PI控制器

理想运放

PI控制器传递函数为：
$-G_c(s)=\frac{Z_f(s)}{Z_{in}(s)}=\frac{R_2}{R_1}+\frac{1}{R_{1}Cs}$
$K_P=\frac{R_2}{R_1}$
$K_i=\frac{1}{R_{1}C}$

因此，PI控制器有一个零点在$f_z=\frac{1}{2\pi R_{1}C}$
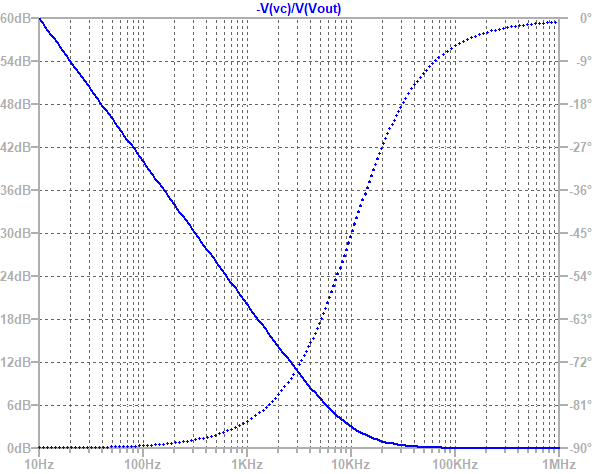
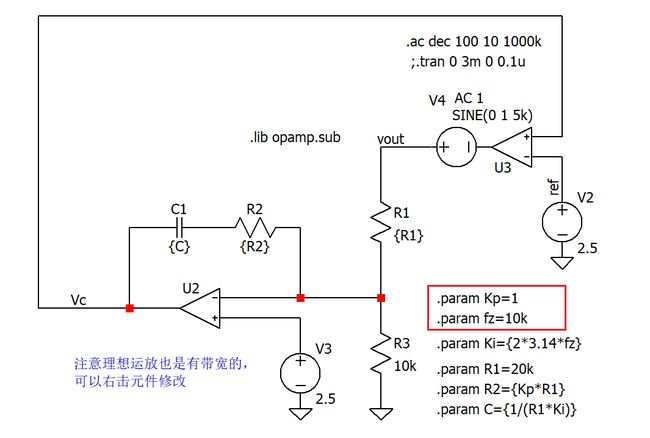
例如，设置Kp=1，fz=10kHz，仿真得到的波特图为：

• 高频增益0dB，即1
• 转折点大致在10kHz

LTspice的理想运放其实也是有带宽和增益的（而不是无穷大），右键点击元件可以修改：

非理想运放

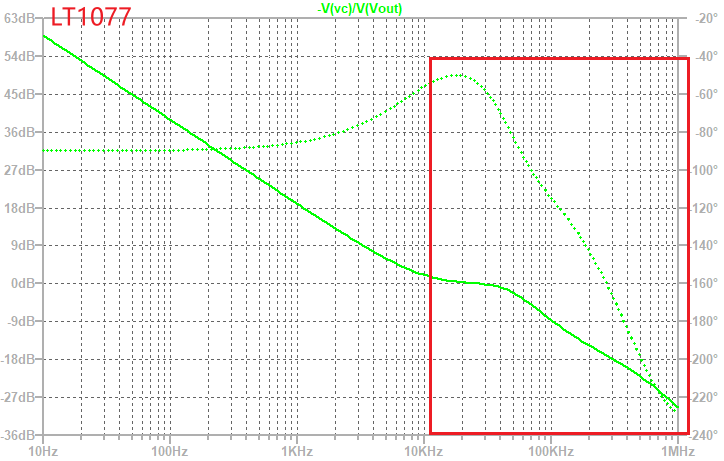
对于实际运放，高频的增益和相位会有明显变化。例如，

• 对于带宽较低的LT1077（增益带宽积250kHz），在30kHz以上，增益和相位都明显偏离理想情况。
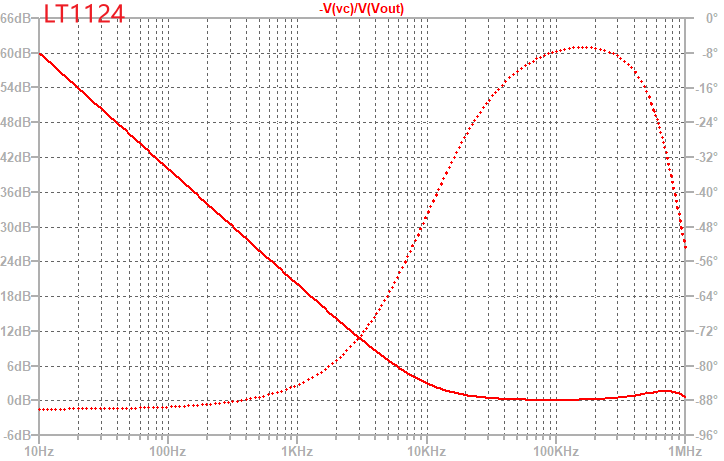
• 带宽较高的LT1124(增益带宽积12.5MHz)，在1MHz以内的增益与理想情况差异不大，但是200kHz以上的相位有较大偏差。

II型控制器

对于II型控制器，

$$\begin{gathered} Z_f(s)=(R_2+\frac{1}{C_{1}s})//\frac{1}{C_{2}s} \\ {Z}_{in}(s)=R_1 \\ -G_c(s)=\frac{Z_f(s)}{Z_{in}(s)}=\frac{C_1{R}_{2}s+1}{R_{1}s(C_1+C_2+C_1{C}_2{R}_{2}s)}\approx \frac{C_1{R}_{2}s+1}{R_1{C}_{1}s(1+C_2{R}_{2}s)} \end{gathered}$$
推导：

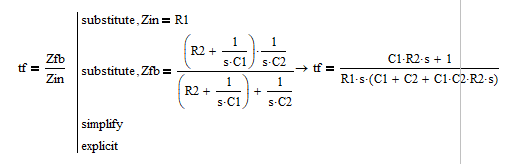
II型控制器有2个极点，极点1为原点，极点2约为$f_{p2}\approx 1/(2\pi C_2{R}_2)$，和1个零点$f_z=1/(2\pi C_1{R}_2)$，其中，零点的频率一般会小于极点2的频率，因此有$C_1>>C_2$。因此能做上面的近似。
此外，频率在$f_z$和$f_{p2}$之间时，控制器的增益约为 $R_2/R_1$。
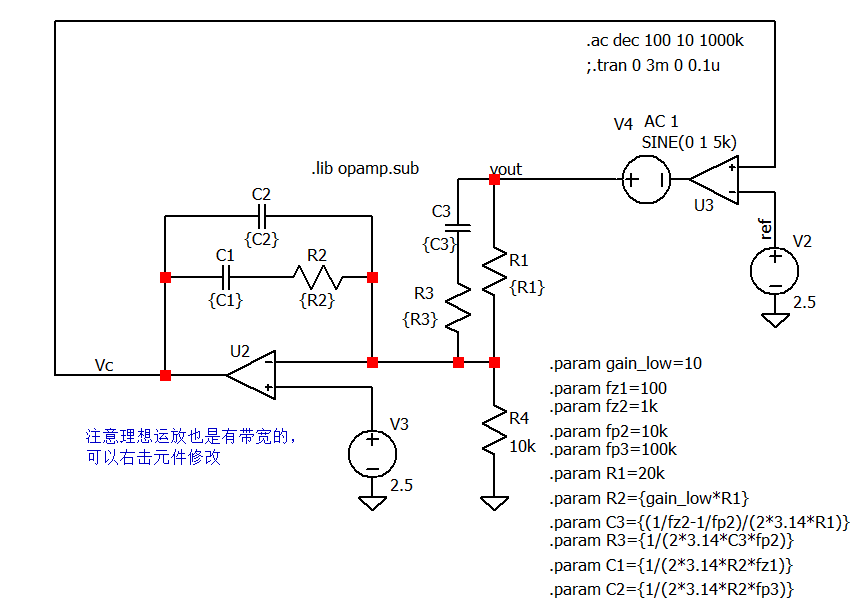
基于这些信息，设计一个中频增益10，零点100Hz，极点10kHz，参数如下图公式：

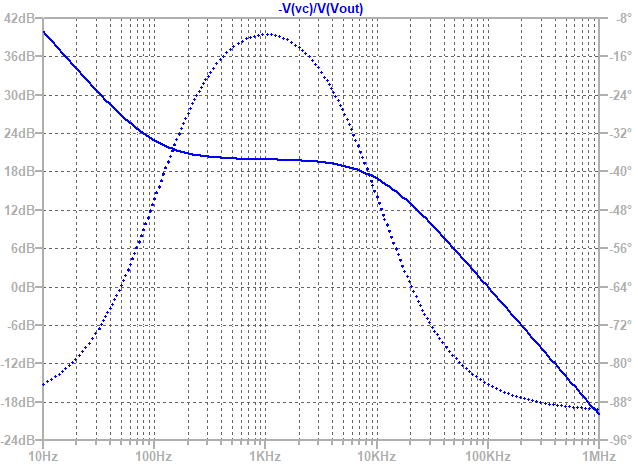
仿真得到的波特图如下： 零点约100Hz，极点约10kHz，中频增益20dB，同设计值。
（具体II型控制器的参数选择还要看相位抬升的度数和抬升处的频率，此处不涉及。）

PID控制器

PID（III型）控制器的传递函数为

$$-G_c(s)=\frac{Z_f(s)}{Z_{in}(s)}=\frac{(C_1{R}_{2}s+1)[C_3(R_1+R_3)s+1]}{R_{1}s(C_3{R}_{3}s+1)(C_1+C_2+C_1{C}_2{R}_{2}s)}\approx \frac{(C_1{R}_{2}s+1)[C_3(R_1+R_3)s+1]}{R_{1}s(C_3{R}_{3}s+1)(C_2{R}_{2}s+1)}$$

推导：

零极点为：

$$\begin{gathered} f_{p1}=0 \\ {f}_{p2}=\frac{1}{2\pi R_3{C}_3} \\ {f}_{p3}=\frac{1}{2\pi R_2{C}_2} \\ {f}_{z1}=\frac{1}{2\pi R_2{C}_1} \\ {f}_{z2}=\frac{1}{2\pi (R_1+R_3)C_3} \end{gathered}$$

低频增益约为$R_2/R_1$（C2和C3开路，C1短路），中频增益约为$R_2/(R_1//R_3)$（C2开路，C1和C3短路）。
例如，选择$f_{z1}=100,f_{z2}=1k,f_{p2}=10k,f_{p3}=100k$, 低频增益$gai{n}_{low}=10$，选定R1=20k，参数计算如下图仿真模型：
其中，C3的计算较为复杂，因为同时与R1和R3有关：
$$C_3=\frac{\frac{1}{f_{z2}}-\frac{1}{f_{p2}}}{2\pi R_1}$$

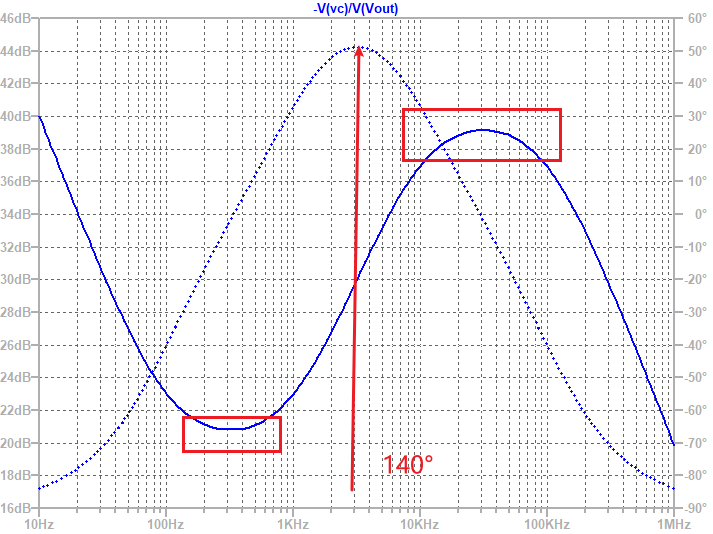
获得的波特图如下：

• 两个零点在100Hz和1kHz附近
• 低频增益约21dB
• 两个极点在1k和10k附近
• 相位抬升约140°
  

总结

• 用LTspice仿真一些控制器的波特图。使用了一个基于理想运放的偏置调节电路，使控制器的输出在一个设定值附近，防止输出饱和影响仿真。
• 简单介绍了PI、II型、III型（PID）控制器的传递函数和参数选择。
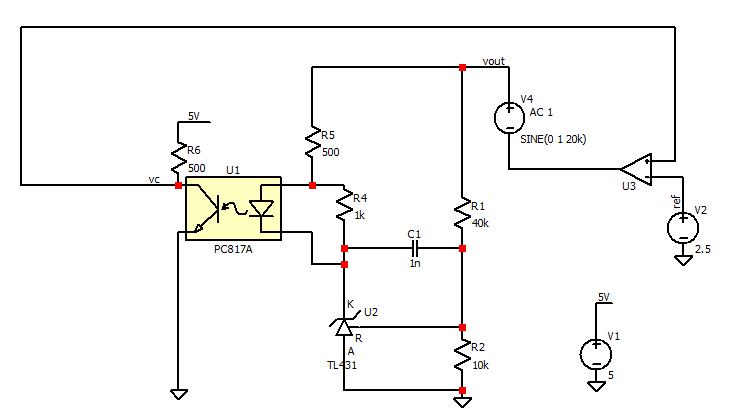
• 保留偏置调节电路并修改补偿器部分，也可以获得其他控制器电路的波特图，比如TL431+光耦：

仿真模型

PI、II型、PID控制器LTspice仿真模型