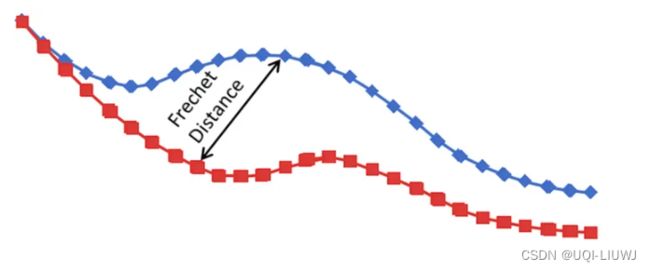
算法笔记：Frechet距离度量

曲线之间相似性的度量，它考虑了沿曲线的点的位置和顺序

1 概念

1.1 直观理解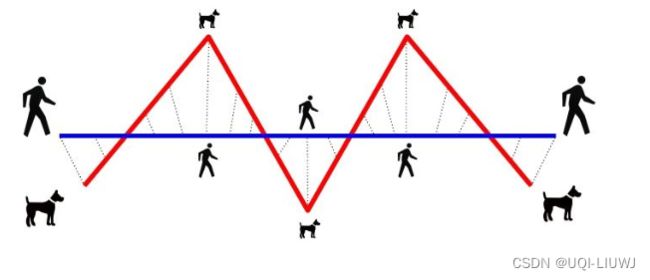

•  主人走路径A，狗走路径B，他们有不同的配速方案
• 主人和狗各自走完这两条路径过程中所需要的最短狗绳长度
  • （在某一种配速下需要的狗绳长度），但其他配速下需要的狗绳长度更长

1.2 数学理解

• 两条曲线A(α(t))和B(β(t))之间距离最大值的下确界
  • t理解为时间
  • α(t)和β(t)理解为人和狗随时间变化的速度
  • A(α(t))和B(β(t))代表t时刻人和狗的位置
  • ——>最大值的下确界意思为,每一种人狗速度方案下，都有对应的距离最大值；那么对于所有的速度方案，这些距离最大值中最小的是哪个？

 

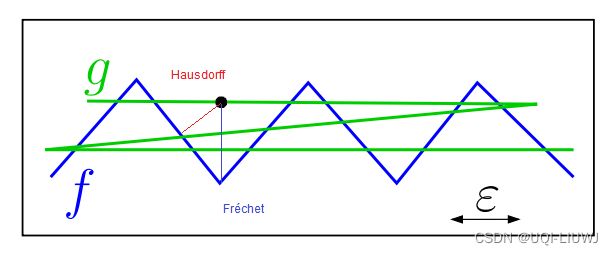
2 和Hausdorff距离的区别

数学笔记/scipy 笔记：豪斯多夫距离（Hausdorff ）_UQI-LIUWJ的博客-CSDN博客

• Fréchet度量考虑到了两条曲线的流动，因为其距离对Fréchet距离有贡献的点对沿着各自的曲线连续扫过。
  • 这使得Fréchet距离比任意点集的Hausdorff距离更能衡量曲线的相似性。
  • 两条曲线有可能有较小的Hausdorff距离，但有较大的Fréchet距离。

   

3 离散化Frechet距离

离散Fréchet距离是连续Fréchet距离的近似，当曲线所选取的离散点足够多时离散Fréchet距离近似等于连续Fréchet距离。

 3.1 python实现

3.1.1 数据集

import numpy as np
a_array = np.array([2, 4, 6, 8])
b_array = np.array([2, 3, 4, 6, 5, 7, 8])

3.1.2 距离函数

#距离函数
def euc_dist(pt1, pt2):
        return np.sqrt(np.square(pt2[0] - pt1[0]) + np.square(pt2[1] - pt1[1]))

 3.1.3 Frechet 距离

def _c(ca, i, j, P, Q):  
        if ca[i, j] > -1:
            return ca[i, j]
        #ca[i,j]之前计算过
        elif i == 0 and j == 0:  
            ca[i, j] = euc_dist(P[0], Q[0])
            #刚刚考虑P序列的0和Q序列的0时
        elif i > 0 and j == 0:  
            ca[i, j] = max(_c(ca, i - 1, 0, P, Q), euc_dist(P[i], Q[0]))
           # 刚刚考虑P序列的i和Q序列的0时
        elif i == 0 and j > 0:  
            ca[i, j] = max(_c(ca, 0, j - 1, P, Q), euc_dist(P[0], Q[j]))
            #刚刚考虑P序列的0和Q序列的j时
        elif i > 0 and j > 0:  
            ca[i, j] = max(min(_c(ca, i - 1, j, P, Q),  # P动Q不动
                               _c(ca, i - 1, j - 1, P, Q),  # P不动Q动
                               _c(ca, i, j - 1, P, Q)),  # 一起动
                           euc_dist(P[i], Q[j]))
            #min是不考虑i，j时，至少需要多长的”狗绳“
            #再取max表示考虑i，j时，需要多长的”狗绳“
        else: 
            ca[i, j] = float("inf")
            # 非法的无效数据，算法中不考虑，此时 i<0,j<0
        return ca[i, j]

def frechet_distance(P, Q):
        ca = np.ones((len(P), len(Q)))
        ca = np.multiply(ca, -1)
        # ca初始化成全-1的矩阵，shape = ( len(a), len(b) )
        dis = _c(ca, len(P) - 1, len(Q) - 1, P, Q)  
        return dis

 3.1.4 计算结果

curve_line_a = list(zip(range(len(a_array)), a_array))
curve_line_b = list(zip(range(len(b_array)), b_array))
#给a,b添加x坐标
curve_line_a
#[(0, 2), (1, 4), (2, 6), (3, 8)]

frechet_distance(curve_line_a,curve_line_b)
#3.0

 4 缺点

• 对噪声很敏感

参考内容：

Frechet distance距离计算原理及python实现_frechet距离_spatial_coder的博客-CSDN博客

曲线相似度衡量——曲线距离计算Fréchet distance详解与python计算-物联沃-IOTWORD物联网

弗雷歇距离 matlab,离散Fréchet（弗雷歇） 距离评价曲线相似度_戴铂的博客-CSDN博客