学习笔记——HYC最棒

深度学习在CV方面的应用

图像识别

告诉你图像是什么

目标定位与检测

准确地找到给定图片中对象的位置，并标出对象的类别。
用的比较多的主要是RCNN，spp- net，fast- rcnn，faster- rcnn；YOLO系列，如YOLO和YOLO9000；除此之外还有SSD，ResNet等。

背景介绍

1. 如何直观的理解 region proposals （候选区域）？
   

• 上图中每一个黄色的框框住的内容都是一个 region propoal ，方方正正的。
• region propoal 通常是使用一种叫 selective search 的方法来确定的。selective search 可以简单的理解为对图片中的每一个像素进行聚类：相邻的相同颜色的像素是一个类别，相邻的相同纹理的像素是一个类别。一个又一个的像素点聚集起来之后就是就变成了上图中一个又一个的块状斑。每一个块状斑就极有可能是我们需要检测的目标。
• 斑的正外接矩形就是我们需要的 region propoal 。
• 块状斑的特点：斑与斑之间的差异较大，斑内的成分与成分之间的差异小。就是低耦合高内聚的意思。

R-CNN

R-CNN 中的 region proposals为后续的CNN网络提供输入。

CNN具有良好的特征提取和分类性能，采用Region Proposal方法实现目标检测问题。算法可以分为三步：

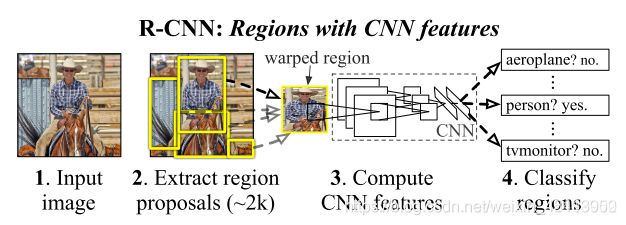
第一步：使用传统方法从原始图片中提取2k个形状大小不统一的 region proposals
第二步：将每一个 region proposal 转变成相同大小（227*227），再使用CNN网络提取特征，输出特征向量。
第三步：使用SVM分类提取出的特征向量（包含背景类别）

RCNN的缺点：
在RCNN刚刚被发明出来的2014年，RCNN在目标检测与行人检测上取得了巨大的成就，然而效率低下，花费时间长等一系列的问题的产生，还是导致了RCNN的运用并没有取得大范围的应用，其最大的问题有三：需要事先提取多个候选区域对应的图像。这一行为会占用大量的磁盘空间；针对传统的CNN来说，输入的map需要时固定尺寸的，而归一化过程中对图片产生的形变会导致图片大小改变，这对CNN的特征提取有致命的坏处；每个region proposal都需要进入CNN网络计算。进而会导致过多次的重复的相同的特征提取，这一举动会导致大大的计算浪费。在这之后，随之而来的Fast RCNN逐渐进入了人们的眼帘。

Fast RCNN

Fast RCNN较之前的RCNN相比，有三个方面得到了提升：

1. 测试时的速度得到了提升。 RCNN算法与图像内的大量候选帧重叠，导致提取特征操作中的大量冗余。 而Fast RCNN则很好的解决了这一问题。
2. 训练时的速度得到了提升。
3. 训练所需的空间大。RCNN中分类器和回归器需要大量特征作为训练样本。而Fast RCNN则不再需要额外储存。

语义分割

从像素级别回答上面两个问题。
在图像领域，语义指的是图像的内容，对图片意思的理解，比如左图的语义就是三个人骑着三辆自行车；分割的意思是从像素的角度分割出图片中的不同对象，对原图中的每个像素都进行标注，比如右图中粉红色代表人，绿色代表自行车。

语义分割中的深度学习技术

1. FCN 全连接
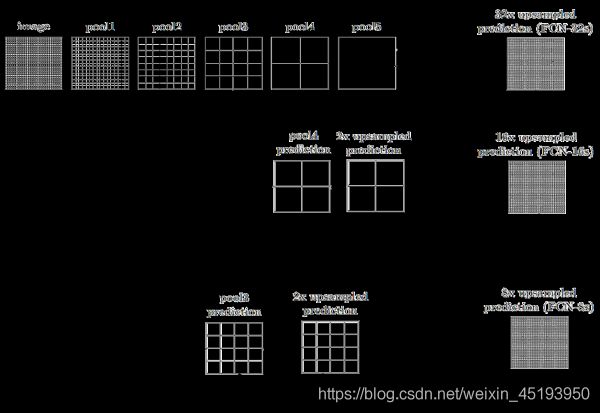
   FCN 所追求的是，输入是一张图片是，输出也是一张图片，学习像素到像素的映射，端到端的映射，网络结构如下图所示：
   
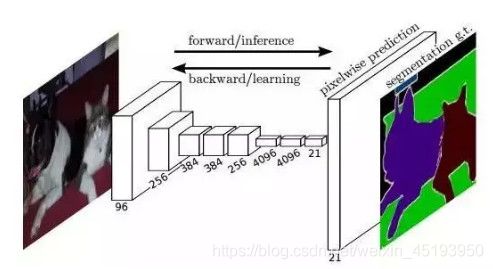
   全卷积神经网络主要使用了三种技术：卷积化（Convolutional）；上采样（Upsample）；跳跃结构（Skip Layer）

• 卷积化即是将普通的分类网络，比如VGG16，ResNet50/101等网络丢弃全连接层，换上对应的卷积层即可。
  
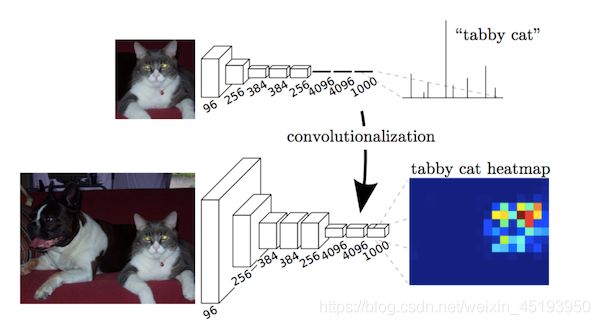
• 在卷积过程中，因为普通的池化会缩小图片的尺寸，比如VGG16 五次池化后图片被缩小了32倍。为了得到和原图等大的分割图，我们需要上采样/反卷积。反卷积和卷积类似，都是相乘相加的运算。只不过后者是多对一，前者是一对多。而反卷积的前向和后向传播，只用颠倒卷积的前后向传播即可。
  
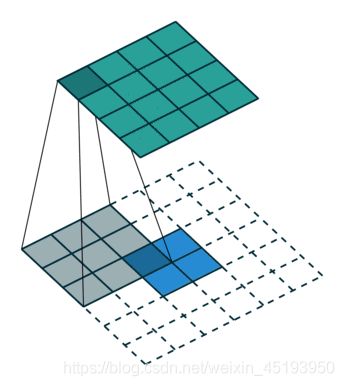
• 跳跃结构（Skip Layer） 这个结构的作用就在于优化结果，因为如果将全卷积之后的结果直接上采样得到的结果是很粗糙的，所以将不同池化层的结果进行上采样之后来优化输出。

而不同上采样结构得到的结果对比如下：

GAN 生成对抗模型

GAN，即生成对抗模型，是图像生成领域内的一种重要方法。GAN是在训练两个相互对抗的网络，一个生成器(Generator)和一个判别器(Descriminator)。当训练达到平衡时，对于一个输入噪声 z。G ( z ) 就是最后生成出来的图像。

原理

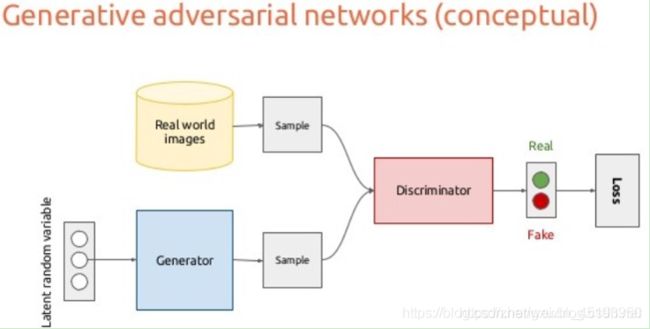
GAN的结构非常简单，就像上图这样，它有一个生成器G（Generator）和一个判别器D（Discriminator）：生成器的输入是一组随机的变量，输出是生成的图；判别器负责对生成的图进行打分，输出是一个0-1之间的置信度。
对于生成器G，希望生成的图像 G ( z )无限逼近于真实图像，而对于判别器D，希望无论生成的图像 G ( z ) 有多真实，判别器总是能把他和真实的图像区分开，所以说GAN是一个G和D博弈的过程。具体如下：

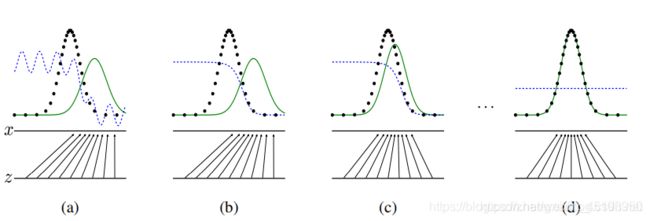
黑线、绿线和蓝线分别代表真实样本分布、生成器生成的样本分布以及判别模型。Z为输入的变量，它映射到x上，用线条来表示一个大致的区间。如蓝色虚线所示，较高的位置表示判别器认为样本来自真实分布，较低位置则来自生成分布。直到蓝色虚线一直处于中间位置，那么它分辨不出两个分布的差别。

• 图(a)是训练前最初的状态;
• 图(b)是固定生成器G，训练判别器D的结果，使判别器可以区分出生生成样本分布和真实样本分布
• 图( c)是固定上一步的判别器D，训练生成器G的结果，使生成的样本分布更接近真实样本分布，骗过当前的判别器；
• (d)是经过多次的迭代，生成器和判别器达到平衡，生产样本无限接近真实样本分布，判别器无法区分出来。

在实际的训练中，生成器G和判别器D的优化不是逐次交替的。而是每训练k次的判别器D后，训练一次生成器G，这样能保证G的变化足够慢，使总是能D保持在其最佳解附近。

损失函数

在 14 年 Goodfellow 等研究者提出来的 GAN 中，它使用 KL 散度度量这种距离。但是原版 GAN 的训练并不稳定，最开始的对抗阶段可能一直生成随机噪声，最后收敛的结果也很可能只生成少量类别的大量重复图像。
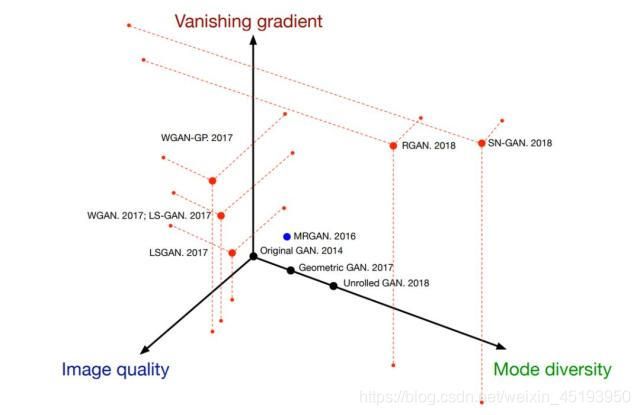
为了解决这一系列问题，生成对抗网络后续也就有了一系列的损失函数创新。，其中有一些耳熟能详的损失函数，例如 Wasserstein 距离、最小二乘距离、几何距离或相对距离等等。总体而言，不同的损失函数主要从梯度消失问题、图像质量和样本多样性三个方面提升 GAN 的效果。
不同的度量方法也会有其独特的角度，例如 WGAN-GP 就特别关注梯度消失问题与图像质量，Spectral normalization GAN 对于处理梯度消失与样本多样性是最高效的。

公式说明：

• x表示真实的图像，z表示输入的G网络噪声，G(z)表示G网络生成的图像。
• 两个“E”表示真实数据和生成数据概率
• D(x)表示真实输入的概率，D(G(z))表示D的鉴别器判断G的生成器生成的图像是真实的概率；
• G的目的：D(G(z))是D网络判断G生成的图片是否真实的概率，G应该希望自己生成的图片“越接近真实越好”。也就是说，G希望D(G(z))尽可能得大，这时V(D, G)会变小。因此我们看到式子的最前面的记号是min_G。
• D的目的：D的能力越强，D(x)应该越大，D(G(x))应该越小。这时V(D,G)会变大。因此式子对于D来说是求最大(max_D)。

公式推导：

训练过程

假设我们定义好了生成器和判别器模型，分别叫做Generator和Discriminator，分别构建它们的optimizer。

#二值交叉熵损失
criterion = nn.BCELoss()
#生成器optimizer
g_optimizer = torch.optim.Adam(Generator.parameters(), lr=0.0002)
#判别器optimizer
d_optimizer = torch.optim.Adam(Discriminator.parameters(), lr=0.0002)
 # 定义真实label为1 可以假设batch_size=1
real_label = Variable(torch.ones(batch_size)).cuda() 
# 定义假的label为0 可以假设batch_size=1
fake_label = Variable(torch.zeros(batch_size)).cuda()  

训练生成器G：

# 生成随机噪声z
z = Variable(torch.randn(batch_size, z_dimension)).cuda()  
# 生成器通过z生成假的图片fake_img 
fake_img = Generator(z)  
# fake_img得到判别结果output 
output = Discriminator(fake_img) 
# output的期望值为1，即real_label，计算生成器损失
# 只有一个损失
g_loss = criterion(output, real_label)   
#优化Generator
g_optimizer.zero_grad() 
g_loss.backward()  
g_optimizer.step() 

训练判别器D：

# 将真实的图片放入判别器中，得到real_out 
real_out = D(real_img)  
# real_out 的期望值为1，即real_label，计算判别器损失1 
d_loss_real = criterion(real_out, real_label)  
# 生成随机噪声z
z = Variable(torch.randn(batch_size, z_dimension)).cuda()  
# 生成器通过z生成假的图片fake_img 
fake_img = G(z) 
# fake_img得到判别结果fake_out 
fake_out = D(fake_img) 
# fake_out 的期望值为0，即fake_label，计算生成器损失
d_loss_fake = criterion(fake_out, fake_label)  
# 将真假图片的loss加起来
# 有两个损失
d_loss = d_loss_real + d_loss_fake  
#优化Discriminator
d_optimizer.zero_grad()  
d_loss.backward()  
d_optimizer.step()  

在训练生成器的时候，对于一个生成的图像，它的期望值是1，这是因为生成器是想尽可能生成一个真实图像。而在训练判别器的时候，对于一个真实图像，它的期望值是1；而对于一个生成的图像（fake_image)，它的期望值是0，是因为判别器要把真实图像和生成的假图像区分出来。要充分理解这是一个“对抗”过程。

评价好坏

在对抗生成网络中，判别器和生成器的目标函数通常都是用来衡量它们各自做的怎么样的。例如，生成器的目标函数用来衡量生成的图片能骗过分类器的性能。
但是这并不能很好的衡量生成图片的质量和多样性。
通常，我们使用IS（inception score）和FID（Fréchet Inception Distance）这两个指标来评价不同的GAN模型。

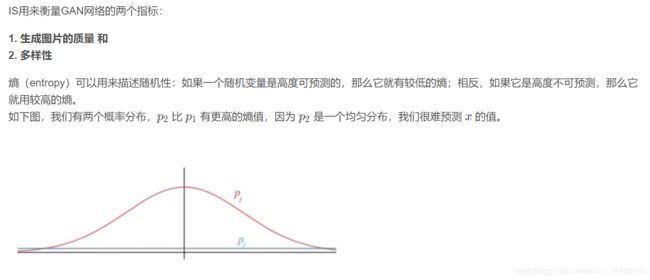
IS（inception score）

FID（Fréchet Inception Distance ）

FID越小，则图像多样性越好，质量也越好
在计算FID中我们也同样使用inception network网络。我们还是先来简单回顾一下什么是inception network，它就是一个特征提取的深度网络，最后一层是一个pooling层，然后可以输出一张图像的类别。在计算FID时，我们去掉这个最后一层pooling层，得到的是一个2048维的高层特征，以下简称n维特征。我们继续简化一下，那么这个n维特征是一个向量。则有：对于我们已经拥有的真实图像，这个向量是服从一个分布的，（我们可以假设它是服从一个高斯分布）；对于那些用GAN来生成的n维特征它也是一个分布；我们应该立马能够知道了，GAN的目标就是使得两个分布尽量相同。假如两个分布相同，那么生成图像的真实性和多样性就和训练数据相同了。于是，现在的问题就是，怎么计算两个分布之间的距离呢？我们需要注意到这两个分布是多变量的，也就是前面提到的n维特征。也就是说我们计算的是两个多维变量分布之间的距离，数学上可以用Wasserstein-2 distance或者Frechet distance来进行计算。以下简单介绍一下如何计算这个距离。

假如一个随机变量服从高斯分布，这个分布可以用一个均值和方差来确定。那么两个分布只要均值和方差相同，则两个分布相同。我们就利用这个均值和方差来计算这两个单变量高斯分布之间的距离。但我们这里是多维的分布，我们知道协方差矩阵可以用来衡量两个维度之间的相关性。所以，我们使用均值和协方差矩阵来计算两个分布之间的距离。均值的维度就是前面n维特征的维度，也就是n维；协方差矩阵则是n*n的矩阵。

最后，我们可以使用下面的公式计算FID:

较低的FID意味着两个分布之间更接近，也就意味着生成图片的质量较高、多样性较好。

FID对模型坍塌更加敏感。相比较IS来说，FID对噪声有更好的鲁棒性。因为假如只有一种图片时，FID这个距离将会相当的高。因此，FID更适合描述GAN网络的多样性。

同样的，FID和IS都是基于特征提取，也就是依赖于某些特征的出现或者不出现。但是他们都无法描述这些特征的空间关系。如下图：

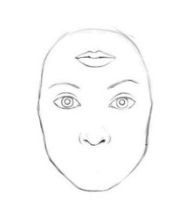
这里我们我们人不会认为这是一张好的人脸图片。但是根据FID和IS，他们就是一个很好的人脸图片。因为它有人脸必要的特征，虽然这些特征的空间关系不好。

往前发展

• styleGAN
• BigGAN
• 新版 BigGAN——BigGAN-deep

条件GAN(Conditional Generative Adversarial Nets)

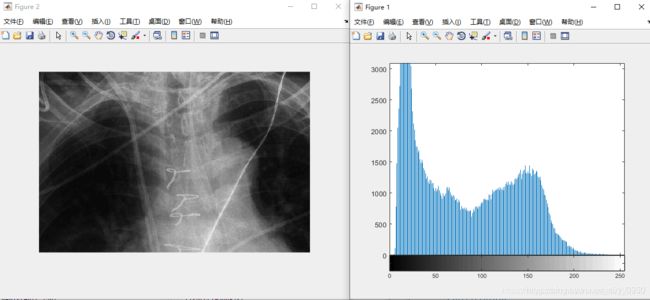
数字图像处理：直方图

简介

灰度级范围为[0,L-1]的数字图像的直方图是离散函数h（rk）=nk，其中rk是第k级灰度值，nk是图像中灰度为rk的像素个数。
在实践中，经常用乘积MN表示的图像像素的总数除它的每个分量来归一化直方图，通常M和N是图像的行和列的维数。因此，归一化后的直方图由p（rk）=nk/MN给出，其中k=0,1,…,L-1。简单来说，p（rk）是灰度级rk在图像中出现的概率的一个估计。归一化直方图的所有分量之和应等于1。
在直方图中，暗图像集中分布在灰度级的低端；亮图像集中分布在灰度级的高端。低对比度图像具有较窄的直方图，且集中于灰度级的中部；高对比度图像的直方图分量则覆盖了很宽的灰度级范围。

##图像对比度指的是一幅图像中明暗区域最亮的白和最暗的黑之间不同亮度层级的测量，即指一幅图像灰度反差的大小。差异范围越大代表对比越大，差异范围越小代表对比越小。
下图就是一个最基本的直方图。

直方图的均衡化

均衡化的基本原理：是把原始图的直方图变换为均匀分布的形式，这样就增加了像素灰度值的动态范围，从而可达到增强图像整体对比度的效果。

均衡化步骤：

1. 统计图像中每个灰度级出现的次数，计算图像中每个灰度级出现的概率；
2. 根据变换公式得到直方图均衡化的变换函数；
3. 根据变换函数映射到每个像素点；输出映射后的图像；

f=imread('#path');
f=rgb2gray(f);
figure,imshow(f);
g=histeq(f,256);#变化函数
figure,imhist(g);
figure,imshow(g);

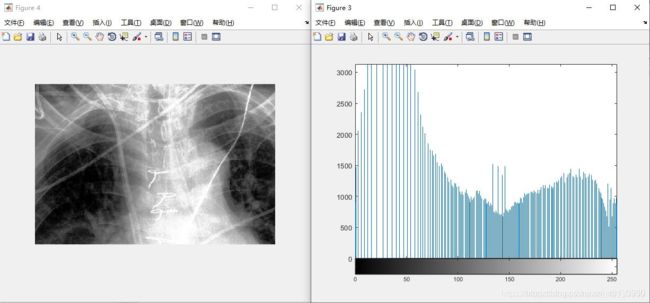
可以看到，均衡化之后的图像，对比度较高，并且其直方图也均匀的分布在了0~255之间。

直方图的规定化

规定化的基本原理：有目的的增强某个灰度区间的图像，即能够人为地修正直方图的形状，使之与期望的图像相匹配。

API序列：别人帮我们写好的一些封装函数

API（Application Programming Interface,应用程序编程接口）是一些预先定义的函数，目的是提供应用程序与开发人员基于某软件或硬件得以访问一组例程的能力，而又无需访问源码，或理解内部工作机制的细节。——百度百科

从文件操作开始谈API。
以C语言为例，我们使用fopen()函数可以打开一个文件，感觉非常简单。文件保存在硬盘上，要经过复杂的处理才能显示，这些细节对我们来说是透明的，由操作系统完成。也就是说，我们调用fopen()函数来通知操作系统，让操作系统打开一个文件。
那么，我们如何告诉操作系统打开文件呢？
看似简单的操作到底层都非常复杂，打开文件首先要扫描硬盘，找到文件的位置，然后从文件中读取一部分数据，将数据放进I/O缓冲区，放进内存；这些数据都是0、1序列，还要对照ASCII表或Unicode表”翻译“成字符，再在显示器上显示出来。这个过程如果要让程序员来完成，那简直是噩梦！
怎么办呢？操作系统想了一个很好的办法，它预先把这些复杂的操作写在一个函数里面，编译成一个组件（一般是动态链接库），随操作系统一起发布，并配上说明文档，程序员只需要简单地调用这些函数就可以完成复杂的工作，让编程变得简单有趣。这些封装好的函数，就叫做API(Application Programming Interface)，即应用程序编程接口。
说得更加通俗易懂一些，别人写好的代码，或者编译好的程序，提供给你使用，就叫做API。你使用了别人代码（或者程序）中的某个函数、类、对象，就叫做使用了某个API。

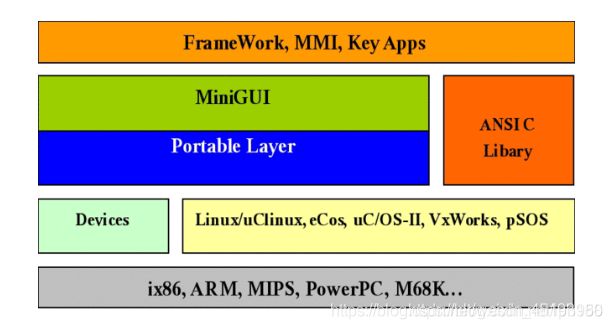
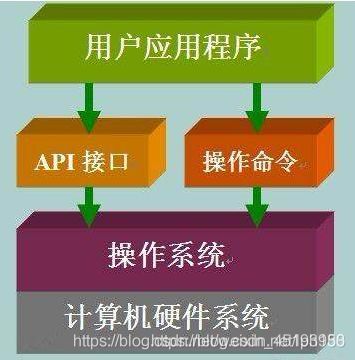
操作系统已经为我们实现了很多功能，它们都被封装成了一个一个的函数，有成百上千个之多，这些函数就叫做 API。程序员要想使用某个功能，只需要调用相应的函数。Windows、Linux、Mac OS、Unix 这些常见的操作系统大部分功能都使用C语言开发，它们的 API 也以C语言的形式呈现。操作系统 API 数目众多，官方必须提供详细的说明文档（Windows API 的说明文档叫 MSDN），程序员在使用 API 时，需要频繁地查阅这些文档。

KNN（K近邻）算法

是个几乎不需要训练就可以得到预测结果的模型。它使用某种方法找到样本空间中距离测试点最近的K个点，以投票表决的方式决定该测试点的标签。

背景介绍

大家通过视频软件挑选电影的时候，通常会先按照电影的类别进行挑选，例如动作片、爱情片、歌舞片。这些电影有各自的特点，像是动作片的打斗场景一定比爱情片多，它也不会像歌舞片一样一言不合就开始跳舞，但又不能完全排除有出现的可能。
总结这三类型的影片所具有的显著特点：打斗、亲吻、跳舞。假设现在用一个元组(a, b, c)来表示，值在0～1之间，Movie = (0.8, 0.1, 0.1)时，就认为这个电影是动作片。那么很自然的，提出了使用一个三维空间作为该数据集的样本空间，每一部电影在空间中都有属于自己的点。

数据集中的数据用三维的样本空间表示，每一个样本都在空间中有唯一的点。

假定现在把一堆电影在这个空间中表示出来，大概率会发现它们具有一定的聚集性，动作片中点与点的距离会比动作片和爱情片中点与点的距离更短。
根据这个特点，提出了K近邻算法。对于给定的一个测试电影，将它在空间中标注出来，使用曼哈顿距离或者欧式距离等，选出K个距离该测试点最近的点，而我们已经事先知道了这些被选出来的最近点的电影类型，接着对其进行类型统计投票，选择票数最多的那个作为该测试电影的类型。
比如当K=5时，用a、b、c分别表示三类型电影的票数，如果a = 4, b = 1, c = 0，我们就认为这部电影是动作片。

从这个过程你可以看出，它只需要一个多维空间、带标签的训练集，因此它也是个有监督学习。

工作原理

1. 首先，存在一个样本数据集合，也称作训练样本集，并且样本集中每个数据都存在标签，即我们知道样本集中每个数据与所属分类的对应关系。
2. 其次，输入没有标签的新数据后，将新数据的每个特征与样本集中数据对应的特征进行比较（计算新数据与训练集中的数据的距离），然后提取样本集中特征最相似数据（最近邻）的分类标签。一般来说，只选择样本数据集中前N个最相似的数据。K一般不大于20。
3. 最后，选择k个中出现次数最多的分类，作为新数据的分类。

K近邻算法的特点也显而易见，由于选择了K个邻近的参考点，因此它的精度较高，且对异常值不敏感，无数据输入假定，使用于数值型和标称型的数据。缺点是计算复杂度和空间复杂度双高。

距离计算

样本之间的距离的计算，我们一般使用对于一般使用Lp距离进行计算。

当p=1时候，称为曼哈顿距离(Manhattan distance)。
当p=2时候，称为欧氏距离(Euclidean distance)。
当p=∞时候，称为极大距离(infty distance)，表示各个坐标的距离最大值,另外也包含夹角余弦等方法。

一般采用欧式距离较多，但是文本分类则倾向于使用余弦来计算相似度。

带有空值的欧式聚类

先计算距离，再填充空值

只计算所有非空的值，对所有空加权到非空值的计算上。
假设此时有x,y两个点，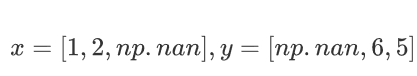
只有第二维全部非空，将第一维和第三维的计算加到第二维上，所有需要乘以3。即：

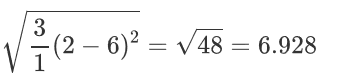
之后进行填充：
需要计算每个样本最近的k个样本，使用简单的加权平均进行填充。
比如当k=2时，样本[1, 2, np.nan] 最近的2个样本是: [3, 4, 3] [np.nan, 6, 5], 计算距离的时候使用欧式距离，只关注非空样本。[1, 2, np.nan] 填充之后得到 [1, 2, (3 + 5) / 2] = [1, 2, 4]。

K值选择

如果选择较小的K值，“学习”的近似误差（approximation error)会减小，但 “学习”的估计误差（estimation error) 会增大，噪声敏感，K值的减小就意味着整体模型变得复杂，容易发生过拟合：

如当K=1时，预测的结果只和最近的一个训练样本相关，此时很容易发生过拟合。

如果选择较大的K值，可以减少学习的估计误差，但缺点是学习的近似误差会增大。K值的增大就意味着整体的模型变得简单。如当K=20时，预测的结果和最近的20个样本相关，假如我们只有20个样本，此时是所有样本的平均值，此时所有预测值都是均值，很容易发生欠拟合。

一般情况下，使用KNN的时候，根据数据规模我们会从[3, 20]之间进行尝试，选择最好的K。