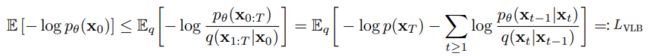Diffusion model之DDPM
Diffusion model之DDPM
- 1.各种生成式模型
- 2.扩散模型DDPM介绍
-
- 2.1 forward process
- 2.2 reverse process
- 2.3 VLB(variational lower-bound)以及训练损失函数
-
- 2.3.1 `negative log-likelihood(NLL) loss`与`VLB`：
- 2.3.2 `VLB`的进一步计算
- 2.3.3 `VLB`中 L t − 1 \large{L}_{t-1} Lt−1项的计算
- 2.3.4 `DDPM`中使用的简化损失函数/训练目标
- 3.训练以及推断
-
- 3.1 训练过程
- 3.2 推断过程
- 参考文献
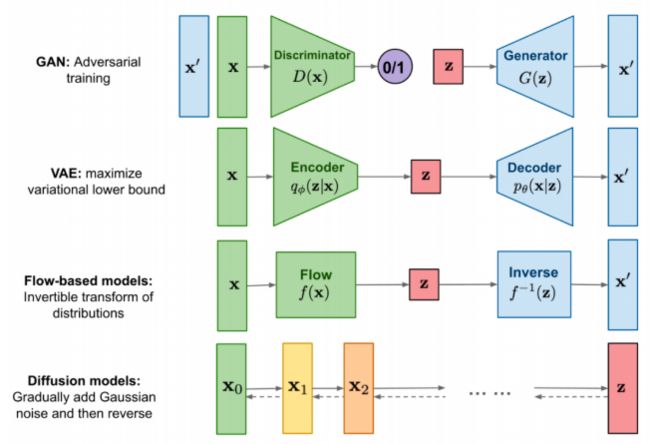
1.各种生成式模型
2.扩散模型DDPM介绍
DDPM(Denoising Diffusion Probabilistic Models)扩散模型由两个过程组成：forward process(diffusion process)以及reverse process。
forward process用于以markov链的形式向原始数据逐渐添加高斯噪声；reverse process接受随机噪声，生成目标数据（如图片）。
本文介绍均以图片为例。
2.1 forward process
涉及公式如下：
X 0 ∼ q ( X 0 ) X_0\sim q(X_0) X0∼q(X0)
q ( X 1 , . . . , X T ∣ X 0 ) : = ∏ t = 1 T q ( X t ∣ X t − 1 ) q(X_{1},...,X_{T}|X_0):=\prod\limits_{t=1}^Tq(X_{t}|X_{t-1}) q(X1,...,XT∣X0):=t=1∏Tq(Xt∣Xt−1)
q ( X t ∣ X t − 1 ) : = N ( X t ; 1 − β t X t − 1 , β t I ) , β t ∈ ( 0 , 1 ) q(X_{t}|X_{t-1}):=\mathcal N(X_{t};\sqrt{1-\beta_t}X_{t-1},\beta_tI),\quad\beta_t\in(0,1) q(Xt∣Xt−1):=N(Xt;1−βtXt−1,βtI),βt∈(0,1)
如果T充分大，并且存在一个好的 β t \beta_t βt函数， X T X_{T} XT会逐渐接近各向同性的高斯分布(isotropic Gaussian distribution)。
α t : = 1 − β t , α ‾ t : = ∏ s = 1 t α s \alpha_t:=1-\beta_t,\overline{\alpha}_t:=\prod\limits_{s=1}^t\alpha_s αt:=1−βt,αt:=s=1∏tαs
q ( X t ∣ X 0 ) : = N ( X t ; α ‾ t X 0 , ( 1 − α ‾ t ) I ) q(X_t|X_0):=\mathcal N(X_{t};\sqrt{\overline{\alpha}_t}X_{0},(1-\overline{\alpha}_t)I) q(Xt∣X0):=N(Xt;αtX0,(1−αt)I)
μ t = 1 − β t X t − 1 , σ t 2 = β t , ϵ ∼ N ( 0 , 1 ) , ∴ X t = 1 − β t X t − 1 + β t ϵ \mu_t=\sqrt{1-\beta_t}X_{t-1},\sigma_t^2=\beta_t,\epsilon\sim\mathcal N(0,1),\therefore X_t=\sqrt{1-\beta_t}X_{t-1}+\sqrt{\beta_t}\epsilon μt=1−βtXt−1,σt2=βt,ϵ∼N(0,1),∴Xt=1−βtXt−1+βtϵ
2.2 reverse process
随机采样一个高斯分布 X T ∼ N ( 0 , 1 ) X_T\sim\mathcal N(0,1) XT∼N(0,1)，如果我们知道条件概率分布 p \large{p} p ( X t ∣ X t − 1 ) (X_t|X_{t-1}) (Xt∣Xt−1)，执行反向的forward process(diffusion process)，就可以获得 X 0 ∼ q ( X 0 ) X_0\sim q(X_0) X0∼q(X0)。
由于条件概率分布很难获得，我们可以通过训练神经网络来获得近似分布 p θ \large{p}_{\theta} pθ ( X t ∣ X t − 1 ) (X_t|X_{t-1}) (Xt∣Xt−1)， θ {\theta} θ表示模型的参数。
假设 reverse process也符合高斯分布，有：
p θ \qquad\qquad\qquad\large{p}_{\theta} pθ ( X t ∣ X t − 1 ) = N ( X t − 1 ; μ θ ( x t , t ) , Σ θ ( x t , t ) ) (X_t|X_{t-1})=\mathcal N(X_{t-1};\mu_{\theta}(x_t,t),\Sigma_{\theta}(x_t,t)) (Xt∣Xt−1)=N(Xt−1;μθ(xt,t),Σθ(xt,t))
DDPM中设 Σ θ ( x t , t ) ) = σ t 2 I \Sigma_{\theta}(x_t,t))=\sigma_t^2I Σθ(xt,t))=σt2I， σ t 2 \sigma_t^2 σt2可以取 β t \beta_t βt或者 β ~ t = 1 − α ‾ t − 1 1 − α ‾ t β t \widetilde{\beta}_t=\cfrac{1-\overline\alpha _{t-1}}{1-\overline\alpha _t} \beta_t β t=1−αt1−αt−1βt。
\qquad\qquad\qquad 其中 α t : = 1 − β t \alpha_t:=1-\beta_t αt:=1−βt， α ‾ t : = ∏ s = 1 t α s \overline{\alpha}_t:=\prod\limits_{s=1}^t\alpha_s αt:=s=1∏tαs
2.3 VLB(variational lower-bound)以及训练损失函数
2.3.1 negative log-likelihood(NLL) loss与VLB：
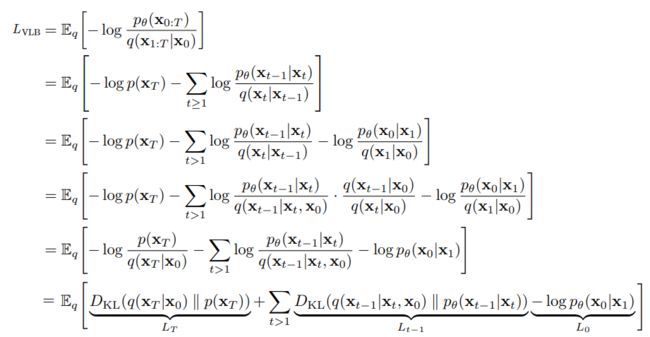
2.3.2 VLB的进一步计算
即：
\qquad\qquad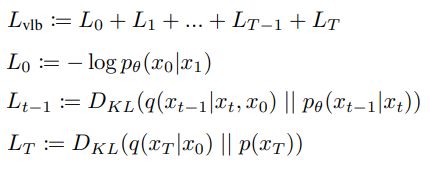 
由于 x T x_T xT是高斯噪音且 q q q无需要学习的参数，因此 L T \large{L}_T LT是常数项，可忽略。
2.3.3 VLB中 L t − 1 \large{L}_{t-1} Lt−1项的计算
L t − 1 \large{L}_{t-1} Lt−1项：
\qquad\qquad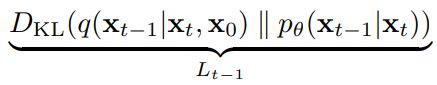 
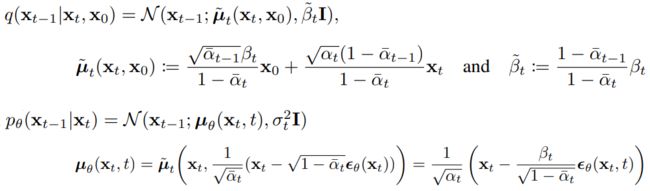
其中 μ ~ t \widetilde{\mu}_t μ t的推导可参考What are Diffusion Models?。
2.3.4 DDPM中使用的简化损失函数/训练目标
DDPM论文中最终建议使用的损失函数同时也忽略了 L 0 \large{L}_0 L0项，
\qquad\qquad 
3.训练以及推断
3.1 训练过程
从数据集中选择图片，使用均匀采用选择一个t值，利用前述损失函数，训练深度学习模型。
3.2 推断过程
随机产生一张符合高斯分布的噪音图片 x T x_T xT，利用迭代公式，迭代T次，获得生成图片 x 0 x_0 x0。
参考文献
[1] Hugging Face：The Annotated Diffusion Model
[2] What are Diffusion Models?
[3] How A.I. Creates Art - A Gentle Introduction to Diffusion Models
[4]diffusion model模型应用与理解
[5] 保姆级讲解 Diffusion 扩散模型（DDPM）
[6] 物理改变图像生成：扩散模型启发于热力学，比它速度快10倍的挑战者来自电动力学
[7] Introduction to Diffusion Models for Machine Learning
[8] Denoising Diffusion Probabilistic Models
[9] PROBABILITY DISTRIBUTIONS
[10] Improved Denoising Diffusion Probabilistic Models
[11] ELBO — What & Why