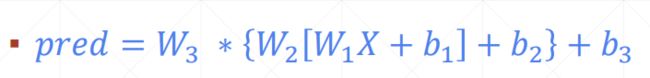Pytorch基础（一）- pytorch介绍，回归和分类问题

Pytorch发展及特点

pytorch在torch7上进行开发的，2018年发布了第一个稳定的版本。

google、TensorFlow基于theano构建。Keras后端为Tensorflow
FaceBook，Amazon
pytorch借鉴了Chainer的API的设计规范。


自然语言处理：AllenNLP
计算机视觉：TorchVision
图卷积神经网络：Fast.ai
部署协议：onnx

通过常用的网络层，堆叠一些复杂的神经网络。

安装好pytorch后查看pytorch版本，是否支持GPU。

import torch
print(torch.__version__)
print(torch.cuda.is_available())

简单回归问题

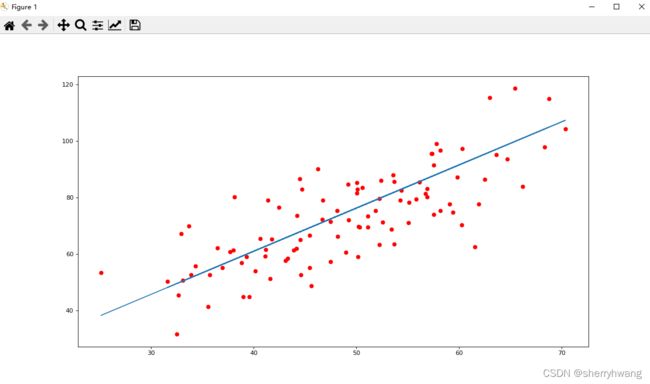
手动实现梯度下降算法求解线性回归问题：
学习率设置为1e-4，迭代次数为1000

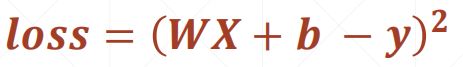
from matplotlib import pyplot as plt
import numpy as np
def update_w_b_step(points, lr, w, b):
    N = len(points)
    for xi,yi in points:
        grad_w = 2/N*((w*xi+b)-yi)*xi
        grad_b = 2/N*((w*xi+b)-yi)
    update_w = w - lr*grad_w
    update_b = b - lr*grad_b
    return update_w, update_b

def gradient_descent(points, w, b, lr, iter):
    for _ in range(iter):
        w,b = update_w_b_step(points, lr, w, b)
    return w,b

if __name__ == '__main__':
    data = np.loadtxt('data.csv', delimiter=',')
    print('running.')
    w,b = gradient_descent(data, 0, 0, 1e-4, 1000)
    print('after finished')
    print(w,b)
    y_pred = [w*i+b for i in data[:,0]]
    plt.figure(figsize=(15,8), dpi=80)
    plt.scatter(data[:,0], data[:,1], color = 'red')
    plt.plot(data[:,0], y_pred)
    plt.show()

输出:
running.
after finished
1.5248459967635082 0.060681971799628164

结果:

手写数字识别

MINIST

非线性因素：

损失函数：

推理：

from statistics import mode
import torch
from torch import nn
import torch.nn.functional as F
from torch import optim

import torchvision
from matplotlib import pyplot as plt 

def one_hot(label, depth=10):
    out = torch.zeros(label.size(0), depth)
    idx = torch.LongTensor(label).view(-1, 1)
    out.scatter_(dim=1, index=idx, value=1)
    return out

def plot_curve(train_loss):
    plt.plot(range(len(train_loss)), train_loss)
    plt.show()

def show_imgs(imgs, labels, name):
    for i in range(6):
        plt.subplot(2, 3, i + 1)
        plt.tight_layout()
        plt.imshow(imgs[i][0]*0.3081+0.1307, cmap='gray', interpolation='none')
        plt.title("{}: {}".format(name, labels[i].item()))
        plt.xticks([])
        plt.yticks([])
    plt.show()

#定义超参数
batch_size = 512
epoch = 3


minist_train = torchvision.datasets.MNIST('minist_data', train=True, download=True,
                                    transform=torchvision.transforms.Compose([
                                        torchvision.transforms.ToTensor(),
                                        torchvision.transforms.Normalize((0.1307,), (0.3081,))
                                    ]))  #下载的图像数据为numpy格式， 转为Tensor， 并且正则化
                                    #下载的图像数据中的像素点为0-1,通过正则化转为0附近的值
minist_test = torchvision.datasets.MNIST('minist_data', train=False, download=True,
                                    transform=torchvision.transforms.Compose([
                                        torchvision.transforms.ToTensor(),
                                        torchvision.transforms.Normalize((0.1307,), (0.3081,))
                                    ]))
train_loader = torch.utils.data.DataLoader(minist_train, batch_size= batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(minist_test,batch_size= batch_size, shuffle=True)


#定义模型
model = nn.Sequential(
    nn.Linear(784, 256),
    nn.ReLU(inplace=True),
    nn.Linear(256, 64),
    nn.ReLU(inplace=True),
    nn.Linear(64, 10),
    # nn.Softmax()    
)

optimizer = optim.SGD(model.parameters(),lr=1e-1)
loss_func = nn.MSELoss()

# 训练
train_loss = []
for i in range(epoch):
    for batch_index, (x, y) in enumerate(train_loader):
         # x: [b, 1, 28, 28], y: [512]
        # [b, 1, 28, 28] => [b, 784]
        x = x.view(x.shape[0],-1)
        out = model(x)
        # [b, 10]
        y_onehot = one_hot(y)
        # loss = mse(out, y_onehot)
        loss = loss_func(out, y_onehot)
        train_loss.append(loss.item())
        optimizer.zero_grad() #清零梯度
        loss.backward()        #计算梯度
        # w' = w - lr*grad
        optimizer.step()       # 更新参数
        if batch_index %10 == 0:
            print(i, batch_index, loss.item())
plot_curve(train_loss)  #绘制损失图像

#计算预测准确度
total_correct = 0
for x,y in test_loader:
    x = x.view(x.shape[0],-1)
    out = model(x)
    # out: [b, 10] => pred: [b]
    pred = out.argmax(dim=1)
    correct = pred.eq(y).sum().float().item()
    total_correct  += correct

total_num = len(test_loader.dataset)
acc = total_correct / total_num
print('test acc:', acc)

#显示图像的预测结果
imgs, label = next(iter(test_loader))
x = imgs.view(imgs.shape[0],-1)
outs = model(x)
show_imgs(imgs, outs.argmax(dim = 1), 'test')

输出:
...
2 80 0.03439983353018761
2 90 0.03506457805633545
2 100 0.034377846866846085
2 110 0.03232051432132721
test acc: 0.8903

绘图结果：