关于DFT预测关于晶格参数、晶体结构、以及相变等简单计算

1周期性结构，超晶胞，晶格参数

从最简单的晶体结构说起，首先要做的是定义纯金属格所有原子的位置：在一个边长为a的立方体中，在每个顶角上面放置一个金属原子，如果采用笛卡尔坐标系，就可以用来定义所有原子的位置，其中为任意整数。这种晶格成为简单立方结构，有一种元素的原子就是按照这种结构进行排列，就是钋。在具体定义一个简单立方晶体结构时，需要的信息就是一个晶格常数a。

假如定义一个原子集合来表示一个简单立方材料用于DFT计算。其实不用具体定义每个原子位置，只需定义最小重复单位的这套原子，那么就可以建立无限大的三维晶体晶体结构。

这个操作分为两步：第一部分，先定义一个体积，使其在所有方向都重复并充满整个空间。对于简单立方金属而言，定义一个边长为a的立方体即可，其中一个原子位于（0,0,0），而顶角的三棱边分别指向三维空间的x,y,z方向。第二部分工作：定义该体积所包含的原子的位置。对于我们现在所考察的简单立方格晶体，在立方体中只包含一个原子，可以将其放置在（0,0,0）位置。把这来那个部分综合起来，就定义了一个简单立方元素的晶体结构。分为两步更好理解，虽然一步也可以。通常，把定义该晶胞体积的矢量，以及晶胞中原子的位置统称为超晶胞，定义超晶胞是DFT计算中最基本的输入和初始化工作。

上面的定义是此种晶体结构所定义的晶胞 包含最少原子数的晶胞，这种超晶胞称为“原胞”。

当然也有很多计算等价的晶胞定义，在此不一一赘述。其实也并不一定非要定义在坐标轴原点，主要这样更美观。其他定义方法并不会改变实际计算结果，只要定义的是同一种晶胞。

假设已经掌握使用DFT程序计算一些原子集合的总能。那么，如何运用总能去确定自然界那些简单立方金属的晶格常数？较为可取的是考察总能和晶格常数的函数关系，即

由于自然界物质能量总是倾向于最小化，所以，根据这些计算可以直接给出一个物理预测，可以由DFT计算预测这个体系总能最低点所对应的晶格常数就是该简单立方材料的晶格常数

为了从总能计算中得到的值，需要了解的函数形式，最简单的表达形式就是把总能写成截断的泰勒展开式为：

式中:,

根据定义，如果是对应于最低能量的晶格常数，则。这表明可以将数据拟合成

式中：,,是拟合参数。

图中黑色实线就是a在2.25-2.6A范围内计算数据拟合后的曲线，该曲线可预测的值是2.43A。

尽管上述等式中把作为拟合参数，但是它实际上具有物理意义。它和材料的平衡态体模量具有关于晶格常数的线性关系。

2面心立方材料

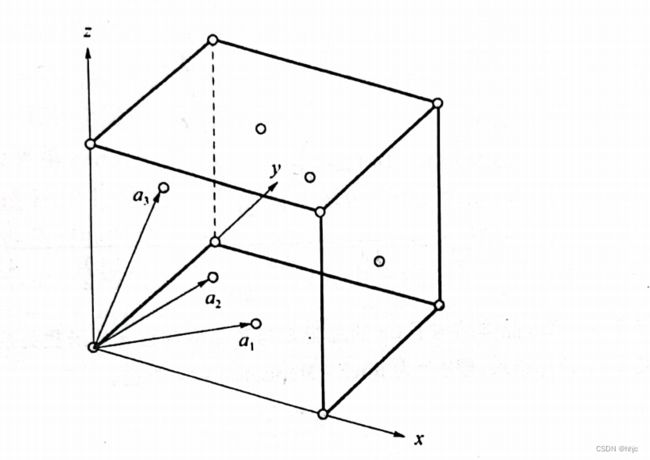
上面讨论的简单立方晶体结构是最简单的晶体结构，但是除了钋之外，没有其他元素以该结构晶体形式存在，因此这种晶体结构作用范围有限。元素周期表中更为常见的面心立方结构（FCC）。对于该晶体结构，可以看做是边长为a立方体的四个顶角和每个面心均有一个原子，这种立方体充满整个空间。对于定义FCC材料的超晶胞，可以在简单立方晶格的基础上，在，

(0.5a,0,0.5a),(0.5a,0.5a,0)。

 图2.定义的FCC金属晶格矢量示意图

（面心立方结构原胞虽然与8个原子接触，但是在实际上，这个原胞只包含4个原子，所以定义一个在原点，三个在面心即可）

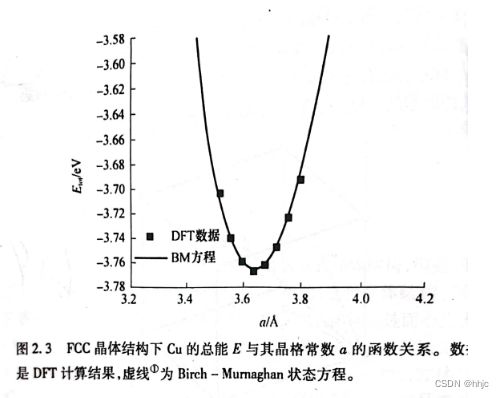
 上图给出了计算得到的FCC Cu总能与其晶格常数之间的函数关系。该曲线形状与Cu在简单立方晶体结构下的相应曲线类似，但是相比于简单立方结构的最小能量，FCC结构的最小能量更低。这一现象可以给出简单的物理解释：FCC晶格结构的Cu要比简单立方结构更为稳定。这个结论在很大程度上也验证了DFT结果的正确性，因为Cu实际上就是FCC金属。预测Cu的晶格常数是3.64A。实验上测得的晶格常数是3.62A。

3密排六方结构

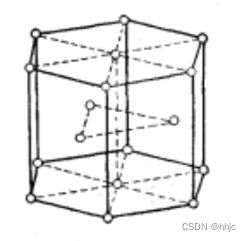
为什么许多金属倾向于FCC结构？其实并不难理解：在空间中堆垛硬球，没有哪种结构比FCC结构更能产生更高的密度，这一结论已被数学证明。但是也存在另外一种堆垛方式，与FCC堆垛具有完全相同的密度，即密排六方结构（HCP）。作为DFT应用的第三种周期性结构，下面对HCP金属进行讨论。

相比于简单立方或者面心立方结构，HCP金属的超晶胞稍微有点复杂

 密排立方结构的晶格参数有两个，由于在实际中密排六方结构的原子并不像简单立方结构和面心立方结构那样每个原子之间距离相等，手里相等，密排立方结构的晶格常数在某一方向上会发生微小畸变，因此导致密排六方结构所需的表征参数有两个。

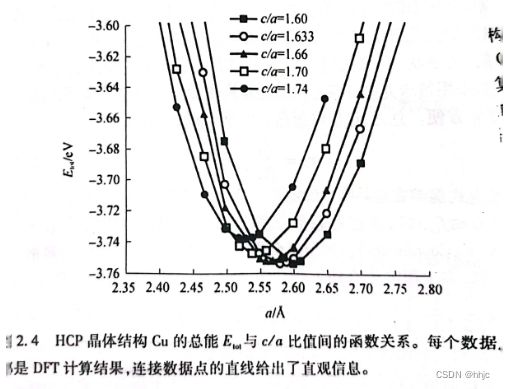
使用DFT计算，可以直接预测Cu在简单立方和FCC晶体结构下的晶格常数。所需的只是一系列总能与晶格常数a的函数关系计算。但是HCP结构具有两个独立参数，就使得这一过程更为复杂。绝大多数DFT软件能够自动处理于此类似的多变量问题

 从上面可以看出在计算下，FCC结构要比HCP结构的 最低总能低0.015ev。因此计算结构和物理实际一致。但是这种能量差别非常微小。

这个计算结果应该让我们思考两件事。第一：DFT计算的数值精确性，是否可以仅依据如此小的能量差值，来判断晶体结构的准确性？ 第二:当晶格参数有两个的时候，计算工作量要比只需确定一个晶格参数的工作量大得多。这也说明：对于一个存在很多自由度的问题，无论这些自由度是超晶胞内的原子位置，还是与晶格矢量相关的晶格参数，即使改变一个参数从而对其总能进行最小化这一做法都难以持续。

4晶体结构预测

根据前文结果，看似已经预测了Cu的晶体结构，但实际有一种马后炮的感觉。因为知识完成了三种晶体结构的对比，在如此繁多的晶体结构中，为什么不会存在另外一种晶体结构使Cu的总能最低？s虽然事实摆在我们眼前，通过实验确实观察到Cu属于FCC金属。

那么假如预测的是没有被实验观察得到的晶体结构呢？多元素合金的结构如何预测？其实也表明现阶段的DFT只能在一系列可能结构下进行预测，并不能准确的预测新型物质的晶体结构。

5相变

以上对于Cu晶体结构的分析全部基于一个思路，即能量最低的晶体结构更有可能在自然界中存在。更准确的说应该是：更容易存在的晶体结构具有较低的吉布斯自由能。吉布斯自由能可以写成：

式中：,V和S分别是材料的内聚能，体积和熵。

如果比较两种可能的晶体结构，则需要计算的是两种结构的吉布斯自由能改变量，即

在固体中，表达式的前两段要比最后一项的贡献大得多。因此有：

在进行DFT计算时，表达式右侧两个能量都有其各自含义。两种结构内聚能的差值就是DFT总能的差值。对于能量曲线上面任意一点，压强可以定义成：

根据1到3节，对于DFT能量与晶格参数之间函数关系曲线图的最小值，可以将其预测为所考察的晶体结构的最优晶格参数。根据上面还可以看出，更准确意思是P=0,V=0最小值所对应的就是最优晶格参数。这个其实也很好理解。P=0意思此时的晶体结构原子不会受其他原子的作用而产生晶格常数偏移。T等于0意味原子停止运动。此时的晶格常数其实就是数学问题的求解。

对于上面的倒数第二个式子，如果,那么两种具有不同内聚能的结构可能具有相同的吉布斯自由能将该条件和下面的式子比较可以看出，如果两种结构的函数关系图中具有相同的正切函数值，则这两种结构就满足上述条件

 其实很好理解，就是把P的偏导带入上面的总能和压强体积等式里面就可以得到这个结论。

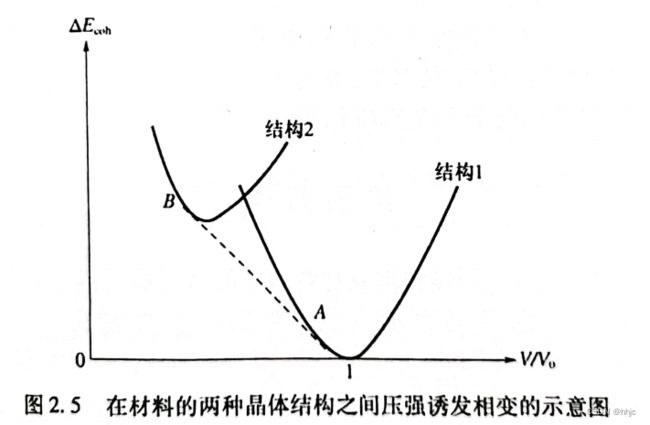
从上面的图可以看到总能最低为V是1的那个点，当沿着曲线向A移动时候，等效于对材料增大压强。当来到A点时候，结构1和2具有相同的正切函数值。当压强足够大的时候，结构2的自由能可定低于结构1的吉布斯自由能

 从这个式子可以看出来。因此根据该图可以预测在这个压强出会发生一个压力诱发的相变，并且相变使内聚能增大，但是在自由能中，增大的内聚能被体积变化的那一项带来的影响给抵消了。

意思就是说，当在这个压强值的时候，物质的体积会收缩，虽然此时物质的总能并不是最小值，但是此时的吉布斯自由能最低，由此晶体结构发生变化，诱发了相变。

许多固体在压力下面都会诱发相变，当然，这个压力也得足够大。