【机器学习】P10 从头到尾实现一个线性回归案例
这里写自定义目录标题
- (1)导入数据
- (2)画出城市人口与利润图
- (3)计算损失值
- (4)计算梯度下降
- (5)开始训练
- (6)画出训练好的模型
- (7)做出预测
- (8)完整代码
(1)导入数据
问题引入:假设你是老板,要考虑在不同的城市开一家新店;
x_train 是不同城市的人口数量
y_train 是那个城市一家餐馆的利润
import math
import copy
import numpy as np
x_train = np.array([6.1101, 5.5277, 8.5186, 7.0032, 5.8598, 8.3829, 7.4764, 8.5781, 6.4862, 5.0546, 5.7107, 14.164, 5.734, 8.4084, 5.6407, 5.3794, 6.3654, 5.1301, 6.4296, 7.0708, 6.1891, 20.27, 5.4901, 6.3261, 5.5649, 18.945, 12.828, 10.957, 13.176, 22.203, 5.2524, 6.5894, 9.2482, 5.8918, 8.2111, 7.9334, 8.0959, 5.6063, 12.836, 6.3534, 5.4069, 6.8825, 11.708, 5.7737, 7.8247, 7.0931, 5.0702, 5.8014, 11.7, 5.5416, 7.5402, 5.3077, 7.4239, 7.6031, 6.3328, 6.3589, 6.2742, 5.6397, 9.3102, 9.4536, 8.8254, 5.1793, 21.279, 14.908, 18.959, 7.2182, 8.2951, 10.236, 5.4994, 20.341, 10.136, 7.3345, 6.0062, 7.2259, 5.0269, 6.5479, 7.5386, 5.0365, 10.274, 5.1077, 5.7292, 5.1884, 6.3557, 9.7687, 6.5159, 8.5172, 9.1802, 6.002, 5.5204, 5.0594, 5.7077, 7.6366, 5.8707, 5.3054, 8.2934, 13.394, 5.4369])
y_train = np.array([17.592, 9.1302, 13.662, 11.854, 6.8233, 11.886, 4.3483, 12., 6.5987, 3.8166, 3.2522, 15.505, 3.1551, 7.2258, 0.71618, 3.5129, 5.3048, 0.56077, 3.6518, 5.3893, 3.1386, 21.767, 4.263, 5.1875, 3.0825, 22.638, 13.501, 7.0467, 14.692, 24.147, -1.22, 5.9966, 12.134, 1.8495, 6.5426, 4.5623, 4.1164, 3.3928, 10.117, 5.4974, 0.55657, 3.9115, 5.3854, 2.4406, 6.7318, 1.0463, 5.1337, 1.844, 8.0043, 1.0179, 6.7504, 1.8396, 4.2885, 4.9981, 1.4233, -1.4211, 2.4756, 4.6042, 3.9624, 5.4141, 5.1694, -0.74279, 17.929, 12.054, 17.054, 4.8852, 5.7442, 7.7754, 1.0173, 20.992, 6.6799, 4.0259, 1.2784, 3.3411, -2.6807, 0.29678, 3.8845, 5.7014, 6.7526, 2.0576, 0.47953, 0.20421, 0.67861, 7.5435, 5.3436, 4.2415, 6.7981, 0.92695, 0.152, 2.8214, 1.8451, 4.2959, 7.2029, 1.9869, 0.14454, 9.0551, 0.61705])
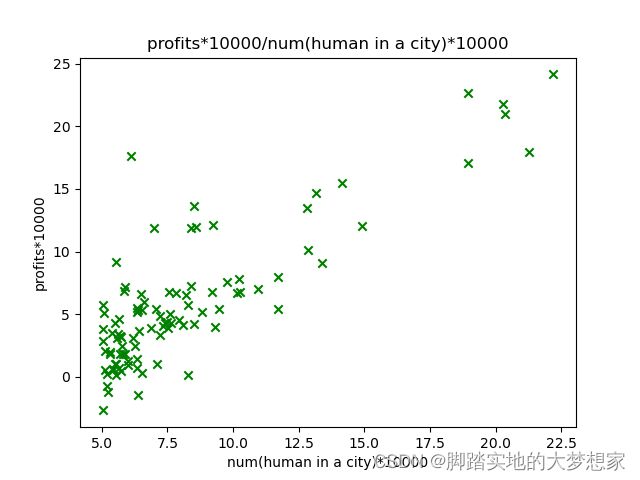
(2)画出城市人口与利润图
通过 python 包 matplotlib.pyplot 画图
import matplotlib.pyplot as plt
plt.scatter(x_train, y_train, marker='x', c='g')
plt.title("利润*10000/人口数量*10000")
plt.ylabel('利润*10000')
plt.xlabel('人口数量*10000')
plt.show()
(3)计算损失值
已知模型为:
f w ⃗ , b ( x ⃗ ( i ) ) = w ⃗ ⋅ x ⃗ ( i ) + b f_{\vec{w},b}(\vec{x}^{(i)}) = \vec{w}·\vec{x}^{(i)}+b fw,b(x(i))=w⋅x(i)+b
损失函数为:
c o s t ( i ) = ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) 2 cost^{(i)} = (f_{\vec{w},b}(\vec{x}^{(i)})-y^{(i)})^2 cost(i)=(fw,b(x(i))−y(i))2
总损失函数为:
J ( w ⃗ . b ) = 1 2 m ∑ i = 0 m − 1 c o s t ( i ) J(\vec{w}.b) = \frac 1 {2m} \sum ^{m-1} _{i=0} cost^{(i)} J(w.b)=2m1i=0∑m−1cost(i)
程序实现如下:
def compute_cost(x,y,w,b):
m = x.shape[0]
total_cost = 0.
for i in range(m):
f_wb = np.dot(w,x[i]) + b
cost = (f_wb - y[i]) ** 2
total_cost += cost
total_cost = total_cost / (2 * m)
return total_cost
(4)计算梯度下降
梯度下降公式为:
repeat until convergence: { 0000 b : = b − α ∂ J ( w , b ) ∂ b 0000 w : = w − α ∂ J ( w , b ) ∂ w } \begin{align*}& \text{repeat until convergence:} \; \lbrace \newline \; & \phantom {0000} b := b - \alpha \frac{\partial J(w,b)}{\partial b} \newline \; & \phantom {0000} w := w - \alpha \frac{\partial J(w,b)}{\partial w} \; & \newline & \rbrace\end{align*} repeat until convergence:{0000b:=b−α∂b∂J(w,b)0000w:=w−α∂w∂J(w,b)}
详解 gradient 部分为:
∂ J ( w , b ) ∂ b = 1 m ∑ i = 0 m − 1 ( f w , b ( x ( i ) ) − y ( i ) ) ∂ J ( w , b ) ∂ w = 1 m ∑ i = 0 m − 1 ( f w , b ( x ( i ) ) − y ( i ) ) x ( i ) \frac{\partial J(w,b)}{\partial b} = \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{w,b}(x^{(i)}) - y^{(i)}) \\ \frac{\partial J(w,b)}{\partial w} = \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{w,b}(x^{(i)}) -y^{(i)})x^{(i)} ∂b∂J(w,b)=m1i=0∑m−1(fw,b(x(i))−y(i))∂w∂J(w,b)=m1i=0∑m−1(fw,b(x(i))−y(i))x(i)
代码实现 gradient 部分:
def compute_gradient(x,y,w,b):
m = x.shape[0]
dj_dw = 0
dj_db = 0
for i in range(m):
f_wb = np.dot(w,x[i]) + b
dj_dw += (f_wb - y[i]) * x[i]
dj_db += f_wb - y[i]
dj_dw = dj_dw / m
dj_db = dj_db / m
return dj_dw, dj_db
代码实现梯度下降 gradient descent:
def gradient_descent(x,y,w_in,b_in,cost_function,gradient_function,alpha,num_iters):
J_history = []
w_history = []
w = copy.deepcopy(w_in)
b = b_in
for i in range(num_iters):
dj_dw, dj_db = gradient_function(x,y,w,b)
w = w - alpha * dj_dw
b = b - alpha * dj_db
if i<100000:
cost = cost_function(x,y,w,b)
J_history.append(cost)
if i% math.ceil(num_iters/10) == 0: # math.ceil: 将传入的参数向上取整为最接近的整数
w_history.append(w)
print(f"Iteration {i:4}: Cost {float(J_history[-1]):8.2f} ")
return w, b, J_history, w_history
(5)开始训练
initial_w = 0.
initial_b = 0.
iterations = 1500
alpha = 0.01
w,b,_,_ = gradient_descent(x_train ,y_train, initial_w, initial_b, compute_cost, compute_gradient, alpha, iterations)
print("w,b found by gradient descent:", w, b)
(6)画出训练好的模型
因为我们已经训练完成模型,所以直接用参数 向量w 与 参数b 的值进行绘图:
m = x_train.shape[0]
predicted = np.zeros(m)
for i in range(m):
predicted[i] = w * x_train[i] + b
plt.plot(x_train, predicted, c = "b")
plt.scatter(x_train, y_train, marker='x', c='g')
plt.title("Profits*10000/Population*10000")
plt.ylabel('Profits*10000')
plt.xlabel('Population*10000')
(7)做出预测
predict1 = 3.5 * w + b
print('For population = 35,000, we predict a profit of $%.2f' % (predict1*10000))
predict2 = 7.0 * w + b
print('For population = 70,000, we predict a profit of $%.2f' % (predict2*10000))
(8)完整代码
import copy
import math
import numpy as np
x_train = np.array([6.1101, 5.5277, 8.5186, 7.0032, 5.8598, 8.3829, 7.4764, 8.5781, 6.4862, 5.0546, 5.7107, 14.164, 5.734, 8.4084, 5.6407, 5.3794, 6.3654, 5.1301, 6.4296, 7.0708, 6.1891, 20.27, 5.4901, 6.3261, 5.5649, 18.945, 12.828, 10.957, 13.176, 22.203, 5.2524, 6.5894, 9.2482, 5.8918, 8.2111, 7.9334, 8.0959, 5.6063, 12.836, 6.3534, 5.4069, 6.8825, 11.708, 5.7737, 7.8247, 7.0931, 5.0702, 5.8014, 11.7, 5.5416, 7.5402, 5.3077, 7.4239, 7.6031, 6.3328, 6.3589, 6.2742, 5.6397, 9.3102, 9.4536, 8.8254, 5.1793, 21.279, 14.908, 18.959, 7.2182, 8.2951, 10.236, 5.4994, 20.341, 10.136, 7.3345, 6.0062, 7.2259, 5.0269, 6.5479, 7.5386, 5.0365, 10.274, 5.1077, 5.7292, 5.1884, 6.3557, 9.7687, 6.5159, 8.5172, 9.1802, 6.002, 5.5204, 5.0594, 5.7077, 7.6366, 5.8707, 5.3054, 8.2934, 13.394, 5.4369])
y_train = np.array([17.592, 9.1302, 13.662, 11.854, 6.8233, 11.886, 4.3483, 12., 6.5987, 3.8166, 3.2522, 15.505, 3.1551, 7.2258, 0.71618, 3.5129, 5.3048, 0.56077, 3.6518, 5.3893, 3.1386, 21.767, 4.263, 5.1875, 3.0825, 22.638, 13.501, 7.0467, 14.692, 24.147, -1.22, 5.9966, 12.134, 1.8495, 6.5426, 4.5623, 4.1164, 3.3928, 10.117, 5.4974, 0.55657, 3.9115, 5.3854, 2.4406, 6.7318, 1.0463, 5.1337, 1.844, 8.0043, 1.0179, 6.7504, 1.8396, 4.2885, 4.9981, 1.4233, -1.4211, 2.4756, 4.6042, 3.9624, 5.4141, 5.1694, -0.74279, 17.929, 12.054, 17.054, 4.8852, 5.7442, 7.7754, 1.0173, 20.992, 6.6799, 4.0259, 1.2784, 3.3411, -2.6807, 0.29678, 3.8845, 5.7014, 6.7526, 2.0576, 0.47953, 0.20421, 0.67861, 7.5435, 5.3436, 4.2415, 6.7981, 0.92695, 0.152, 2.8214, 1.8451, 4.2959, 7.2029, 1.9869, 0.14454, 9.0551, 0.61705])
import matplotlib.pyplot as plt
plt.scatter(x_train, y_train, marker='x', c='g')
plt.title("profits*10000/num(human in a city)*10000")
plt.ylabel('profits*10000')
plt.xlabel('num(human in a city)*10000')
plt.show()
def compute_cost(x, y, w, b):
m = x.shape[0]
total_cost = 0.
for i in range(m):
f_wb = np.dot(w, x[i]) + b
cost = (f_wb - y[i]) ** 2
total_cost += cost
total_cost = total_cost / (2 * m)
return total_cost
def compute_gradient(x,y,w,b):
m = x.shape[0]
dj_dw = 0
dj_db = 0
for i in range(m):
f_wb = np.dot(w,x[i]) + b
dj_dw += (f_wb - y[i]) * x[i]
dj_db += f_wb - y[i]
dj_dw = dj_dw / m
dj_db = dj_db / m
return dj_dw, dj_db
def gradient_descent(x, y, w_in, b_in, cost_function, gradient_function, alpha, num_iters):
J_history = []
w_history = []
w = copy.deepcopy(w_in)
b = b_in
for i in range(num_iters):
dj_dw, dj_db = gradient_function(x, y, w, b)
w = w - alpha * dj_dw
b = b - alpha * dj_db
if i < 100000:
cost = cost_function(x, y, w, b)
J_history.append(cost)
if i % math.ceil(num_iters / 10) == 0: # math.ceil: 将传入的参数向上取整为最接近的整数
w_history.append(w)
print(f"Iteration {i:4}: Cost {float(J_history[-1]):8.2f} ")
return w, b, J_history, w_history
initial_w = 0.
initial_b = 0.
iterations = 1500
alpha = 0.01
w,b,_,_ = gradient_descent(x_train ,y_train, initial_w, initial_b, compute_cost, compute_gradient, alpha, iterations)
print("w,b found by gradient descent:", w, b)
m = x_train.shape[0]
predicted = np.zeros(m)
for i in range(m):
predicted[i] = w * x_train[i] + b
plt.plot(x_train, predicted, c = "b")
plt.scatter(x_train, y_train, marker='x', c='g')
plt.title("Profits*10000/Population*10000")
plt.ylabel('Profits*10000')
plt.xlabel('Population*10000')
plt.show()
predict1 = 3.5 * w + b
print('For population = 35,000, we predict a profit of $%.2f' % (predict1*10000))
predict2 = 7.0 * w + b
print('For population = 70,000, we predict a profit of $%.2f' % (predict2*10000))