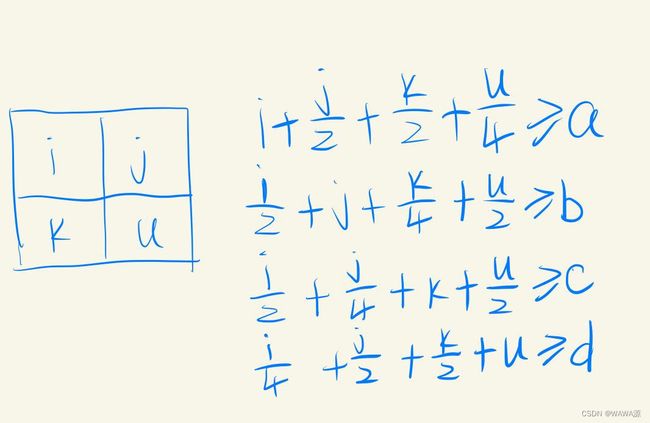2022学年第一学期郑州大学ACM招新赛&选拔赛

A SW的与众不同数组 — 签到

一共n个数， 用set无重复值的性质统计一下有几个不同的数，记为 res
n - res 如果是偶数 每次删除两个刚好可以，如果是奇数需要再删除一个不重复的数完成对应操作

#include 
#include 
using namespace std;
void solve()
{
	int n; cin >> n;
    set<int> mp;
    for(int i = 0, x; i < n; i ++) cin >> x, mp.insert(x);
    
    int res = mp.size();
    if((n - res) % 2 == 1) res --;
    cout << res << '\n';
}
signed main()
{
	int T; cin >> T;
	while(T --) solve();
} 

B WASD机器人 — 暴力/ 数学推导

暴力写法：

直接暴力枚举 最后成功到达终点的 串中的 L/R 的数量，这样的话 L, R, U, D的数量全都可以确定下来了，然后每次更新答案，取最小值

#include 
#include 
using namespace std;
signed main()
{
    string s; cin >> s; 
    int n = s.size();
    int x, y; cin >> x >> y;
    if(abs(x) + abs(y) > s.size()) return puts("-1"), 0;
    
    // 现有的 l, r, u, d 的数量
	int nl = 0, nr = 0, nu = 0, nd = 0;
    for(auto c : s)
	{
		nl += c == 'L';
		nr += c == 'R';
		nu += c == 'U';
		nd += c == 'D';
	}	
	
	int res = n;
	// 枚举最后结果中  l, r 数量 此时 u, d 数量也确定了
	int l, r, u, d;
	for(int i = 0; i <= n; i ++)
	{
		if(x > 0) l = i, r = x + i;
		else l = -x + i, r = i;
		
		int dt = (n - l - r - y) / 2;
		if(y > 0) u = y + dt, d = dt;
		else u = dt, d = -y + dt;
		
        if(l < 0 || r < 0 || d < 0 || u < 0 ) break;
		int sum = abs(nl - l) + abs(nr - r) + abs(nu - u) + abs(nd - d);
		res = min(res, (sum + 1) / 2); 
	} 
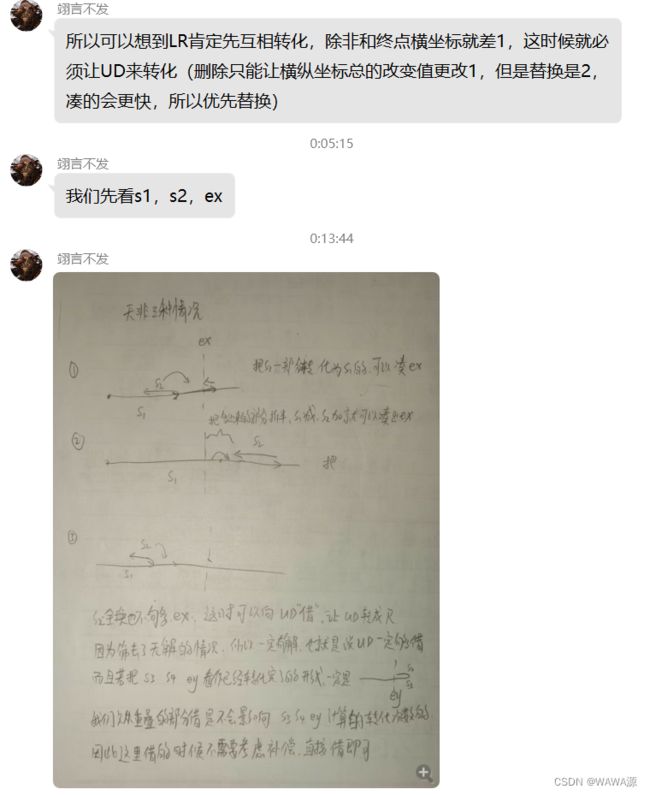
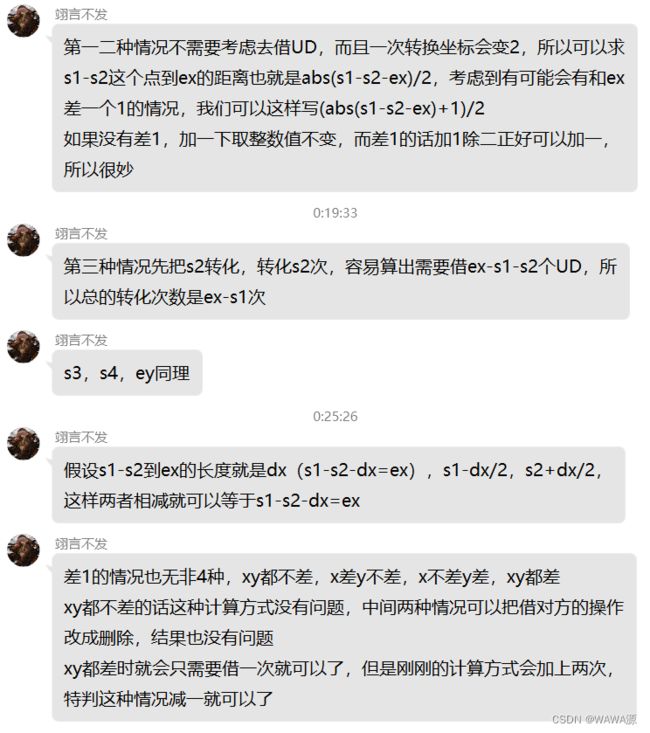
	cout << res << '\n';
}

数学写法 放上吕翊加大佬的推导过程

#include 
#include 
using namespace std;
int sum[5];
int main()
{
    string s; cin >> s;
    for (int i = 0; i < (int)s.size(); ++ i)
    {
        if (s[i] == 'R') ++ sum[1];
        if (s[i] == 'L') ++ sum[2];
        if (s[i] == 'U') ++ sum[3];
        if (s[i] == 'D') ++ sum[4];
    }
    int tx, ty; cin >> tx >> ty;
    if (abs(tx) + abs(ty) > sum[1] + sum[2] + sum[3] + sum[4]) return puts("-1"), 0;
    if (tx < 0)
    {
        tx = -tx;
        swap(sum[1], sum[2]);
    }
    if (ty < 0)
    {
        ty = -ty;
        swap(sum[3], sum[4]);
    }
    int ans = 0;
    if (sum[1] + sum[2] < tx) ans += tx - sum[1];
    else ans += (abs(sum[1] - sum[2] - tx) + 1) / 2;
    if (sum[3] + sum[4] < ty) ans += ty - sum[3];
    else ans += (abs(sum[3] - sum[4] - ty) + 1) / 2;
    if (abs(sum[1] - sum[2] - tx) % 2 && std::abs(sum[3] - sum[4] - ty) % 2) -- ans;
    cout << ans << '\n';
}

C SW的糖果树（困难版本）— 启发式合并优化

思路和简单暴力版一样 只是多了启发式合并
这里大概说一下为什么可以用启发式合并， 因为每个子节点遍历完后就不会再遍历了，如果不进行启发式合并就相当于把子节点对应的子树信息 更新到父节点上，但是可能存在父节点存的信息更少，如果把子节点信息更新到父节点上就会变慢，所以可以进行启发式合并进行优化，复杂度$O(nlogn)$

#include 
#include 
#include 
#include 
#include 
using namespace std;
const int N = 100010; 
int n, a[N], res = 0;
bool st[N];
vector<int> g[N];
map<int,int> mp[N];
int maxv[N], maxv_col[N], sum[N];

void dfs(int u)
{
	st[u] = true;
	mp[u][a[u]] ++;
	maxv[u] = 1;
	maxv_col[u] = a[u];
	sum[u] = a[u];
	
	for(auto v : g[u])
	{
		if(st[v]) continue;
		dfs(v);
        // 启发式合并操作
		if(mp[u].size() < mp[v].size()) 
		{
			swap(mp[u], mp[v]);
			swap(maxv[u], maxv[v]);
			swap(maxv_col[u], maxv_col[v]);
			swap(sum[u], sum[v]);
		}
		
		for(auto [x, c] : mp[v])
		{
			if(mp[u][x] == 0) sum[u] ^= x;
			mp[u][x] += c;
			if(mp[u][x] > maxv[u])
			{
				maxv[u] = mp[u][x];
				maxv_col[u] = x;
			}
			else if(mp[u][x] == maxv[u]) maxv_col[u] ^= x;
		}
	}
	res = max(sum[u] ^ maxv_col[u], res);
}

signed main()
{
	cin >> n;
	for(int i = 1; i <= n; i ++) cin >> a[i];
	for(int i = 1, u, v; i < n; i ++)
	{
		cin >> u >> v;
		g[u].push_back(v);
		g[v].push_back(u);
	}
	dfs(1);
	cout << res << '\n';
}

D SW的七星光芒剑 — 数学

找到6个点 连接6条线
需要注意的是 每行*之间有 空格

#include 
#include 
using namespace std;
char g[1010][1010];
signed main()
{
	int n; cin >> n;
    memset(g, ' ', sizeof g);
    
	for(int i = 1; i <= 6 * n - 5; i ++) if(i & 1) g[n][i] = g[3 * n - 2][i] = '*';
	for(int i = 1, j = 3 * n - 2; i <= 3 * n - 2; i ++, j --) g[i][j] = '*';
	for(int i = 1, j = 3 * n - 2; i <= 3 * n - 2; i ++, j ++) g[i][j] = '*';
	for(int i = 4 * n - 3, j = 3 * n - 2; i >= n; i --, j --) g[i][j] = '*';
	for(int i = 4 * n - 3, j = 3 * n - 2; i >= n; i --, j ++) g[i][j] = '*';
	
    for(int i = 1; i <= 4 * n - 3; i ++)
    {
        for(int j = 1; j <= 6 * n - 5; j ++)
			cout << g[i][j];
		cout << '\n';
    }
} 

E 井字棋游戏 — 博弈论+ 暴搜

因为要判断a1是否必胜 因此 对于 a1 而言 平局算输，而对于a2而言平局算赢
直接dfs出每种情况 做一个判断，如果存在赢的情况就赢，如果 一种情况都不赢就输
即 有一种必胜就是 必胜 所有必败就是必败

#include 
using namespace std;
#define int long long

int g[10];
// 判断是否获胜
bool win(int x)
{
	for(int i = 0; i < 7; i += 3)
		if(g[i] == x && g[i + 1] == x && g[i + 2] == x) return true;
	for(int i = 0; i < 3; i ++)
		if(g[i] == x && g[i + 3] == x && g[i + 6] == x) return true;
	if(g[0] == x && g[4] == x && g[8] == x) return true;
	if(g[2] == x && g[4] == x && g[6] == x) return true;
	return false;
}
// 1: 输/平局 0，赢1
// 2: 赢/平局 1, 输0
bool dfs()
{
	int a1 = 0, a2 = 0;
	for(int i = 0; i < 9; i ++)
	{
		a1 += g[i] == 1;
		a2 += g[i] == 2;
	}
    // 最后一步是 p2走的，只要不是p1 赢 p1 就算输
	if(a1 + a2 == 9) return !win(1);
	// 轮到a1
	if(a1 == a2)
	{
		if(win(1)) return true;
		if(win(2)) return false;
		bool f = 0;
		for(int i = 0; i < 9; i ++)
		{
			if(g[i]) continue;
			g[i] = 1;
            // 如果存在a2 输了 ，则a1赢
			if(dfs() == false) f = 1;
			g[i] = 0;
			if(f) return true;
		}
        // 如果 a2一直赢 则 a1 必输
		return false;
	}
	// 先到轮到 a2  与 a1 同理
	else
	{
		if(win(2)) return true;
		if(win(1)) return false;
		bool f = 0;
		for(int i = 0; i < 9; i ++)
		{
			if(g[i]) continue;
			g[i] = 2;
			if(dfs() == false) f = 1;
			g[i] = 0;
			if(f) return true;
		}
		return false;
	}
}
signed main()
{
	int a1 = 0, a2 = 0;
    for(int i = 0; i < 9; i ++)
    {
    	cin >> g[i];
    	a1 += g[i] == 1;
    	a2 += g[i] == 2;
	}
    int res = dfs();
    // 看残局先手是谁， 如果是p2 需要异或一下答案
    if(a1 != a2) res ^= 1;
    cout << (res ? "YES" : "NO") << '\n';
}

F SW的糖果树（简单版本）— 暴力

这个题意思容易理解错
意思是 求 把一个子树中最大数量的所有颜色去掉 ，求其它颜色的异或和 的 最大值
直接暴力每个子树顶点，然后统计这个子树中最大数量的颜色 再异或去掉

#include 
#include 
#include 
using namespace std;
#define int long long
const int N = 10010;
int a[N];
vector<int> g[N];
bool st[N];
map<int,int> mp[N];
int res = 0;
void dfs(int u, int fa)
{
    st[u] = true;
    for(auto v : g[u])
    {
    	if(v == fa || st[v]) continue;
        dfs(v, u);
        // 把子树中颜色加到父亲节点颜色中
        for(auto [x, c] : mp[v])
            mp[u][x] += c;
    }
    mp[u][a[u]] ++;
    vector<int> vec;
    // 统计出现最多的颜色
    int maxv = 0, s = 0;
    for(auto [x, c] : mp[u])
    {
        if(maxv < c) vec.clear(), maxv = c;
        if(maxv == c) vec.push_back(x);
        s ^= x;
    }
    // 把出现最多的颜色去掉
    for(auto x : vec) s ^= x;
    
    res = max(res, s);
}
signed main()
{
	int n; cin >> n;
    for(int i = 1; i <= n; i ++) cin >> a[i];
    for(int i = 1, u, v; i < n; i ++)
    {
        cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    dfs(1, -1);
    cout << res << '\n';
} 

G 凑数字 — 构造

n,n-1这两个数不变, 前面全部凑成1，相邻两个相减为1， 然后1 * 1，最后(1 + n - 1) * n

#include 
#include 
#include 
using namespace std;
signed main()
{
	int n; cin >> n;
    if(n == 2)
    {
        cout << -1 << '\n';
        return 0;
    }
	int m = n - 2;
    vector<string> res;
    for(int i = m; i > 1; i -= 2)
    {
        string s = to_string(i) + " - " + to_string(i - 1);
        res.push_back(s);
    }
    
    while(res.size() < n - 3) res.push_back("1 * 1");
    string s = "1 + " + to_string(n - 1); res.push_back(s);
    s = to_string(n) + " * " + to_string(n); res.push_back(s);
    
    for(auto x : res) cout << x << '\n';
} 

H 旋转数组 — dp

这个一定要读清楚题 连续上升子串 是指 数值连续 1，2，3，4…且位置连续
状态表示：
$dp[i][j]$表示 以i列结尾，且数值为j的最长字串长度
状态转移：
$dp[j+1][x]=max(dp[j+1][x],dp[j][x-1]+1)$

#include 
#include 
#include 
using namespace std;
const int N = 100010;
vector<vector<int>> a;
map<int,int> dp[N];
int n, m;
int res = 0; 
signed main()
{
    cin >> n >> m;
    a = vector<vector<int>> (n, vector<int>(m));
    for(int i = 0; i < n; i ++)
        for(int j = 0; j < m; j ++)
            cin >> a[i][j];
    
	for(int j = 0; j < m; j ++)
		for(int i = 0; i < n; i ++)
		{
			int x = a[i][j];
			dp[j + 1][x] = max(dp[j + 1][x], dp[j][x - 1] + 1);
			res = max(res, dp[j + 1][x]);
		}
	cout << res << '\n';
}

I 最小字典序序列 — 小项堆 + 栈 模拟题

这就是个模拟题，开m个栈，记录每个栈 栈顶数值 对应的栈的编号pos
同时维护一个小项堆，每次从小项堆里拿出最小值放入结果中，同时根据pos找到最小值对应的栈的编号，将栈更新

#include 
#include 
#include 
#include 
using namespace std;
const int N = 100010;
int pos[N];
stack<int> stk[N];
signed main()
{
	int n, m; cin >> n >> m;
	priority_queue<int, vector<int>, greater<int> > heap;
	for(int i = 1; i <= m; i ++)
	{
		int t, x; cin >> t;
		while(t --) cin >> x, stk[i].push(x);
		pos[x] = i; heap.push(x);
	}
	
	string res = "";
	while(heap.size())
	{
		int t = heap.top(); heap.pop();
		res += " " + to_string(t);
		if(stk[pos[t]].size()) stk[pos[t]].pop();
		if(stk[pos[t]].size())
		{
			int top = stk[pos[t]].top();
			heap.push(top);
			pos[top] = pos[t];
		}
	}
    cout << res.substr(1) << '\n';
} 

J SW玩扫雷 — 模拟签到

直接模拟，遍历到每个雷，把周围的数值都+1

#include 
#include 
using namespace std;
char g[110][110];
int res[110][110];
signed main()
{
    memset(res, 0, sizeof res);
    int n, m; cin >> n >> m;
    for(int i = 1; i <= n; i ++) cin >> (g[i] + 1);
    
    // 设置个负无穷 最后做判断
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++)
            if(g[i][j] == '*') res[i][j] = -1e9;
    
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++)
            if(g[i][j] == '*')
                // 相邻8个数
                for(int u = i - 1; u <= i + 1; u ++)
                    for(int v = j - 1; v <= j + 1; v ++)
                    {
                        if(u == i && j == v) continue;
                        res[u][v] ++;
                    }
    
    for(int i = 1; i <= n; i ++)
    {
        for(int j = 1; j <= m; j ++)
            if(res[i][j] >= 0) cout << res[i][j];
            else cout << "*";
        cout << '\n';
    }
} 

K 亮度 — 暴力

推个数学式子然后暴力， 四维可优化到三维 见代码

#include 
#include 
#include 
using namespace std;
signed main()
{
	int a, b, c, d; cin >> a >> b >> c >> d;
    int res = 10000;
    for(int i = 0; i <= 500; i ++)
    {
        if(i > res) break;
        for(int j = 0; j <= 500; j ++)
        {
            if(i + j > res) break;
            for(int k = 0; k <= 500; k ++)
            {
                if(i + j + k > res) break;
                int t1 = (a - (i + j / 2 + k / 2)) * 4;
                int t2 = (b - (i / 2 + j + k / 4)) * 2;
                int t3 = (c - (i / 2 + j / 4 + k)) * 2;
                int t4 = (d - (i / 4 + j / 2 + k / 2));
                int u = max({t1, t2, t3, t4});
                res = min(res, i + j + k + u);
            }
        }
    }
    cout << res << '\n';
} 

L SW的妙妙区间 — 思维

这里放一道同类型力扣题，可以做一下传送门

正难则反的思路 ， 我们可以先找不包含0的区间，再用总区间减去
不包含0的区间求解思路
先枚举右端点i，此时右端点固定 找符合条件的左端点数量 加到res中， 离右端点最远的左端点就是到最近的一个包含0的区间，可以用map判断是否包含包含0， map储存前缀和，如果map出现两个相同的值就证明有0出现了，用pos记录最近的0的位置

#include 
#include 
#include 
using namespace std;
#define int long long
const int N = 1000010;
int a[N];
signed main()
{
	int n; cin >> n;
    for(int i = 1; i <= n; i ++) cin >> a[i];
    int res = 0;
    unordered_map<int,int> mp;
    for(int i = 0, pos = 0, sum = 0; i <= n; i ++)
    {
        sum += a[i];
        if(mp.count(sum)) pos = max(pos, mp[sum] + 1);
        mp[sum] = i;
        res += i - pos;
    }
    cout << (n + 1) * n / 2 - res << '\n';
}