动态规划-不相交的线
动态规划-不相交的线
- 前言
动态规划中存在一类问题,它涉及到两个数组或链表,需要求解出两个数组中的最长公共子序列,如果要求解两个数组的最长公共子序列。如果采取最原始的方式,选择对第一个数组中的元素的不同排列进行有序组合枚举(subset),类似采用Powerset的求解方法,紧接着采用KMP方法,在第二个数组中搜索所有的可能的subset序列,优点是理解直观,也容易编程实现;缺点也显而易见,时间和空间复杂度都很高,尤其是时间复杂度,保持在指数级别。
- 不相交的线 问题描述
问题来源于Leetcode - 1035,
在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
现在,可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线,这些直线需要同时满足满足:
nums1[i] == nums2[j]- 且绘制的直线不与任何其他连线(非水平线)相交。
请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。
以这种方法绘制线条,并返回可以绘制的最大连线数。
这个问题其实可以归结为最长公共子序列问题,由于为最长公共子序列,采用最长公共子序列对应元素绘制的直线不会与其它连线相交,因为公共子序列的搜索是线性模式,一旦搜索完成,不会进行回退处理。
- 问题解答
基于《算法导论》中CRCC的四步方法模板,我们对此问题进行深入剖析和理解。第一步为表征最优子问题的解结构(Characterize the structure of the optimal solution),最优子问题一般表现为求最大、最小或者满足特定条件的解数量。
a.) 表征最优子问题的解结构
首先我们需要找到子问题的表征方式,如果采用F(i,j)来表征可以绘制的最大连线数,那么子问题有哪些呢? 我们分为2种不同情况来分别探讨,
- 如果nums1[i]的元素和nums2[j]的元素,二者互相相等,这种情况下,F(i,j)问题的值就需要依赖F(i-1,j-1),然后再加上1即可。也可以理解此时,问题规模都缩小1,同时,带来的连线数目也相应增加1.
- 如果nums2[i]位置上元素和nums2[j]元素不相等,这种情况下,F[i,j]的值就依赖于F(i-1,j)或F(i,j-1),如果把F(i-1,j)或F(i,j-1)的描述可视化,意思就是两个数组当前位置元素既然不等,那么F(i-1,j)就表示nums1中的元素回退一个位置,然后再和数组nums2的元素进行比较;F(i,j-1)表示数组nums1元素位置保持不变,让nums2当前元素位置回退1,然后在进行相关的比较。
此时子问题的结构就显现出来,原来的问题可能是三个子问题中的任何一个,所以在程序中需要采用判断进行计算,由于判断的条件为相等或者不相等,那么整个问题的递归在空间上就构造出一颗二叉树(严格意义上来说,是带条件的的动态二叉树)。
b.) 采用递归的方式定义最优解(Recursively define the value of the optimal problem)
递归问题需要采用“从大处着眼,从小处着手”的原则,头脑中谨记递归的全局观念,那么此问题的大处可以表征为F(i,j) 其中i表示nums1的元素下标,j表示nums2的下标,按照上面的条件:
F ( i , j ) = { F ( i − 1 , j − 1 ) } + 1 ; i f n u m s 1 [ i ] = = n u m s 2 [ j ] F ( i , j ) = m a x { F ( i − 1 , j ) , F ( i , j − 1 ) } n u m s 1 [ i ] ≠ n u m s 2 [ j ] F(i,j)=\{F(i-1,j-1)\}+1;\ if \ nums1[i]==nums2[j] \\F(i,j)=max\{F(i-1,j),F(i,j-1)\} \ nums1[i]≠nums2[j] F(i,j)={F(i−1,j−1)}+1; if nums1[i]==nums2[j]F(i,j)=max{F(i−1,j),F(i,j−1)} nums1[i]=nums2[j]
采用递归定义的问题中,我们发现存在求最大值的问题,同时也有选择带来绘制线条数目增加的问题,其代价是1而已。接下来,自然而然会有问题,递归当中是否存在重合的子问题呢? 答案是肯定的,只是比较隐蔽而已。采用画图的方式对此进行进一步的解释和深入的理解。
红色椭圆内的两个子问题,可以归结问同一个问题,也就是此问题展现出重叠子问题的基本特征。有了重叠子问题和最优解结构两大特征,我们可以声明此问题可以采用动态规划加以解决。
c) 计算最优解的值(Compute the value of the optimal solution),一般情况下可以选择递归或迭代方式。
如果要采用递归的方式,那么就需要确定递归出口条件,经过上图观察发现,当任意一个数组中的元素个数为0的时候,此时返回0的值。这个其实也非常容易理解,如果某个数组不含有元素,那么就无法进行元素之间的连线,所以结果自然而然等于0.
递归过程中,实际上由于条件的判定,递归树出现了剪枝,剪枝的导致的结果使三叉树直接退化为二叉树或线性表(单树)。我们可以看到F(nums1[1],nums2[1,3,9])实际上是单个树,其后由于条件不同,又演化为二叉树。
d) 代码实现
代码实现过程非常简单,采用naive的递归方式,理解简单原始的问题解决方式。
函数实现代码:
/**
* @file max_uncrossed_lines.c
* @author your name ([email protected])
* @brief
* @version 0.1
* @date 2023-03-27
*
* @copyright Copyright (c) 2023
*
*/
#ifndef MAX_UNCROSSED_LINES_C
#define MAX_UNCROSSED_LINES_C
#include "max_uncrossed_lines.h"
int max_uncrossed_lines(int *nums1, int *nums2, int i, int j)
{
if(i==0 || j==0)
{
return 0;
}
int max_lines;
int line_1;
int line_2;
if(nums1[i-1]==nums2[j-1])
{
max_lines=max_uncrossed_lines(nums1,nums2,i-1,j-1)+1;
}
else
{
line_1 = max_uncrossed_lines(nums1, nums2, i - 1, j);
line_2 = max_uncrossed_lines(nums1, nums2, i, j - 1);
max_lines=(line_1>=line_2?line_1:line_2);
}
return max_lines;
}
#endif
测试代码
/**
* @file max_uncrossed_lines_main.c
* @author your name ([email protected])
* @brief
* @version 0.1
* @date 2023-03-27
*
* @copyright Copyright (c) 2023
*
*/
#ifndef MAX_UNCROSSED_LINES_MAIN_C
#define MAX_UNCROSSED_LINES_MAIN_C
#include "max_uncrossed_lines.c"
int main(void)
{
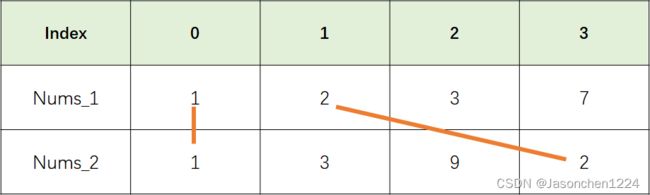
int nums1[] = {1,2,3,7};
int nums2[] = {1,3,9,2};
int nums1_size=sizeof(nums1)/sizeof(int);
int nums2_size = sizeof(nums2) / sizeof(int);
int max_value;
max_value=max_uncrossed_lines(nums1,nums2,nums1_size,nums2_size);
printf("The max number of uncrossed line is %d\n",max_value);
getchar();
return EXIT_SUCCESS;
}
#endif
- 小结
面对不相交的线问题,我们转换为LCS问题,利用剪枝条件,把三叉树退化为二叉树或线性列表,这个过程中不断利用剪枝条件对问题进行深度优先遍历,最后结合各个子问题的解,得到最原始问题的答案。
参考资料:
1035. 不相交的线 - 力扣(Leetcode)