多项式拟合
文章内容部分参考:建模算法入门笔记-多项式拟合(附源码) - 哔哩哔哩 (bilibili.com)
(9条消息) 数学建模——人口预测模型公有木兮木恋白的博客-CSDN博客数学建模人口预测模型
多项式拟合是数据拟合的一种,与插值有一定区别(插值要求曲线经过给定的点,拟合不一定经过给定的点)
介绍MATLAB中三种多项式拟合的方法——代码法、代码窗口法、窗口法。
根据这个例子进行三种方法的分析:给定以下点(1,9)(2,5)(3,4)(4,4)(5,2)(6,3)(7,2)(8,4)(9,9),要求进行多项式拟合,求出x=5.5、x=10时的y值。
分析之前要在matlab绘制散点图:
方法一:通过plot函数画离散点图
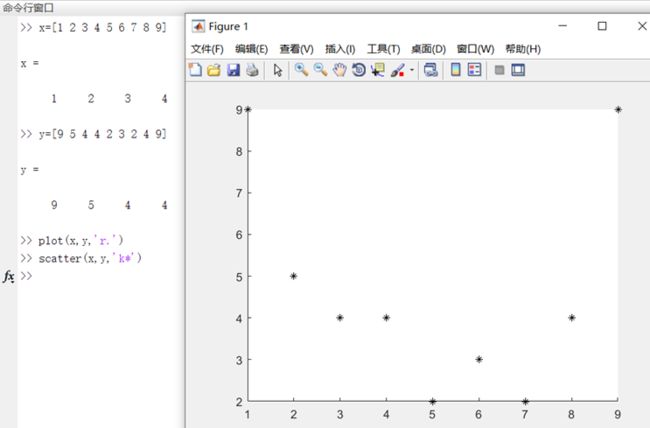
打开matlab,在命令行窗口中输入“x=[1 2 3 4 5 6 7 8 9] y=[9 5 4 4 2 3 2 4 9]”创建离散点数据,需要注意x,y长度一致
然后输入plot(x,y,’r.'),其中r是代表红色,后面的点是绘制的离散点形状,如图:
方法二:通过scatter函数画离散点图
在命令行窗口中输入“scatter(x,y,'k*')”
可以由图看出,题目给点分布散乱,且x=5.5与x=10的点都不存在,这时需要拟合曲线,根据曲线的函数,求出对应的y值(x=5.5在所给x区间[1,9]内,这时求对应的y值为内插法,反之x=10在区间外,此时求y值为外插法。一般用拟合法求内插,外插法多为预测类。
一、代码法
MATLAB代码如下:(使用时只需修改部分数据即可)
x=[123456789];
y=[954423249];
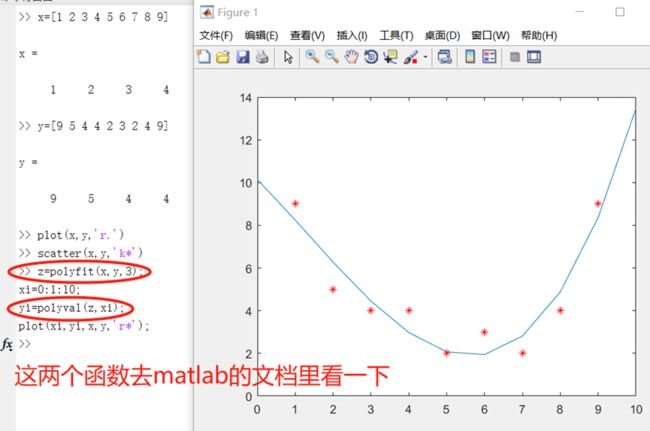
z=polyfit(x,y,3);
xi=0:1:10;
yi=polyval(z,xi);
plot(xi,yi,x,y,'r*');其中,z=polyfit(x,y,3);的3指拟合的最高次幂为3,该最高次幂需要不断调整,以得出最佳拟合方案。
据图可以读出,x=5.5时y约为2,x=10时y约为13.5
该方法较为简便,但是需要自行修改、调整函数系数,而且不能得出拟合曲线的具体函数值。
二、代码窗口法
先输入以下代码,绘出点图:
x=[123456789];
y=[954423249];
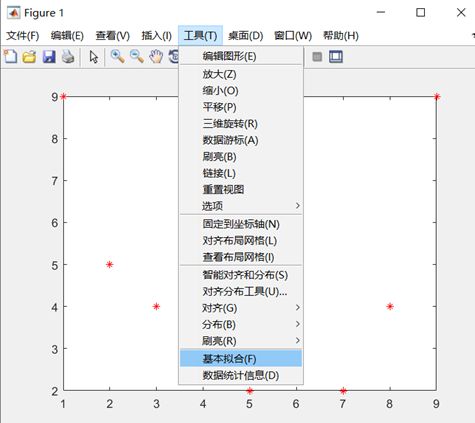
plot(x,y,'r*')然后按下面的操作来即可:
一个是样条插值,一个是三次方拟合
不同的拟合方法对应的函数都不同,根据函数图像,估计对应的y值即可
三、窗口法
值得注意的是:上述两种方法都能方便地得到函数图像,但是却不能得到具体的拟合函数表达式。而窗口法却能快速得到表达式(但是有的表达式的系数是以概率表达的)。
首先输入给定的x值与y值:x=[1 2 3 4 5 6 7 8 9];y=[9 5 4 4 2 3 2 4 9];
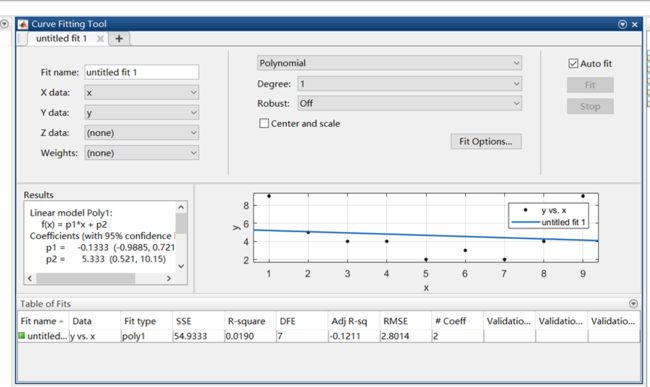
再点击APP栏的Curve Fitting栏
令X data为x,Y data为y后,选择拟合方式即可,本图为一次线性拟合
三次拟合
图像左侧的Results栏是输出的函数表达式,注意其系数是按照概率选取的:
Linear model Poly3:
f(x) = p1*x^3 + p2*x^2 + p3*x + p4
Coefficients (with 95% confidence bounds):
• p1 = 0.03535 (-0.04166, 0.1124)
• p2 = -0.1407 (-1.308, 1.026)
• p3 = -1.795 (-6.95, 3.36)
• p4 = 10.14 (3.856, 16.43)具体的拟合函数表达式需要视所用的拟合方法的不同而定。
处理人口模型
1、假设
把人口增长看做是一个多项式函数
人口增长没有限制,可以一直增长
2、特点
已有数据拟合的很好,不论数据有没有规律可言
预测未来一两年比较准确,越往后越不准确
预测的人口数量在未来会超出人口限制,且增长速度变快
3、代码实现
以年份为x轴变量,当年人口为y轴变量,将两者进行拟合得到人口数模型与时间的关系式,选取某城市2008到2019年老年人口数量进行模拟测试
首先是将已有的数据拟合成一条曲线,过程代码如下所示
close
clc;
clearall %清除所有
n=5;%拟合多项式的次数
year=2008:2019;
num=[97.42102.36 105.78 111.16 116.04 121.71 126.26 134.93 137139141.89146];%户籍人口;
p5= polyfit(year,num,n); %5阶拟合
%绘制原始数据和拟合曲线图
figure(1)
holdon;
xlabel('year'); %设置横坐标名
ylabel('num'); %设置纵坐标名
title('2008-2019人口增长曲线'); %设置标题
gridon %网格线
plot(year,num,'r*',year,polyval(p5,year))
legend('人口数量','拟合曲线')然后预测未来几年的人口增长数
figure(2)
year1=2008:2025;
plot(year1,polyval(p5,year1))
people=polyval(p5,year1);
legend('人口预测数量')