数学建模论文写作

声明：本文为本人在b站学习清风数学建模的学习笔记
数学建模清风——论文写作方法教程（国赛和美赛）

论文写作方法

国赛

摘要

摘要的开头段

开头段：

需要充分概括论文内容，一般两到三句话即可长度控制在三至五行。

第一句话可以简单交代下题目的背景 (可选) ;

第二句话交代你们所做的事情 (必须) ;第三句话可以说下解决这个问题的实际意义 (少部分有)。

(重要性: 第二句话>第一句话>第三句话)

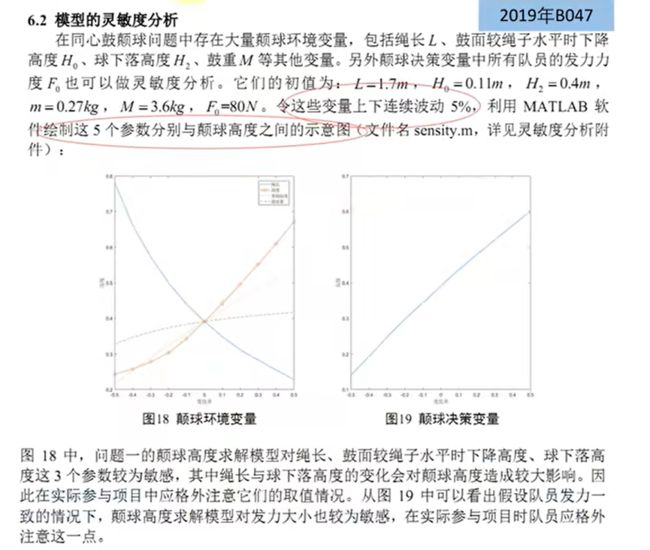
例1 (19b) :

同心鼓”游戏是一项团队协作能力拓展项目，队员通过拉绳使鼓抬高，达到使球在鼓面上跳动的目的。

本文通过建立三维物理模型，利用数学物理方法，分析了“同心鼓”游戏中的物理过程。

该问题的研究能为游戏参与者提供指导性意见，帮助参与者取得更好成绩。

例2(19c)：

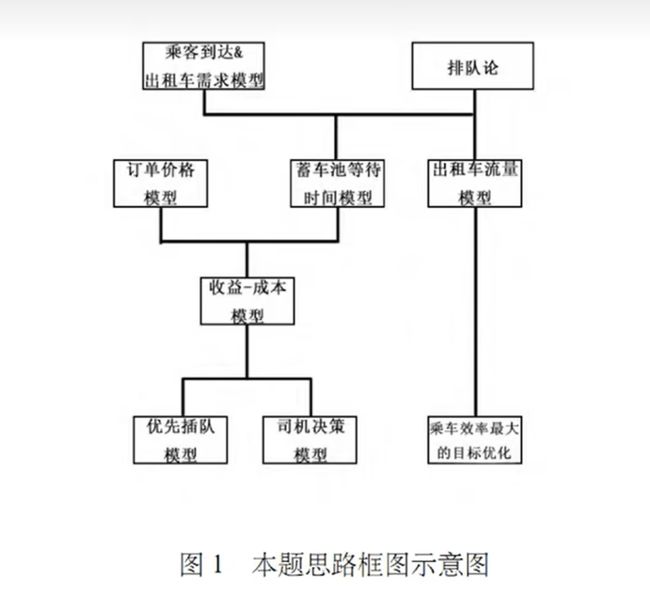
本文针对送客到机场后出租车司机的决策问题，基于排队论、收益与成本博弈，建立了数学模型，为出租车

司机提供了选择决策，给出了总乘车效率高时的乘车点安排以及有“优先权”的出租车安排方案。

例3 (19e)：

“薄利多销”原则被广泛运用于现代商场的促销中，研究商品的折扣力度与销量的关系对扩大商品的销量与提高

商场的获益有实际意义。

本文围绕薄利多销的分析问题，基于对附件中数据挖掘分析并借助于 SPSS 等软件，给出了商场每天的营业

额、利润率以及打折力度，并运用回归分析建立了打折力度与商品销售额以及利润率的统计模型。

摘要的中间段

中间段：

需要对每个问题分别进行叙述，一般需要包含下面三要素:

• 解决了什么问题
• 应用了什么方法
• 得到了什么结果

(1) 解决了什么问题?

有三种方式提出：

直接用一句话概括题目要我们求解的问题。 (较少见到)

不单独提出我们要解决的是什么问题，因为在后面的两个要素中也会提到。 (最常见到)

可以指出题目中问我们的是什么类型的问题，例如常见的有预测类、评价类、规划优化类。 (极少见到)

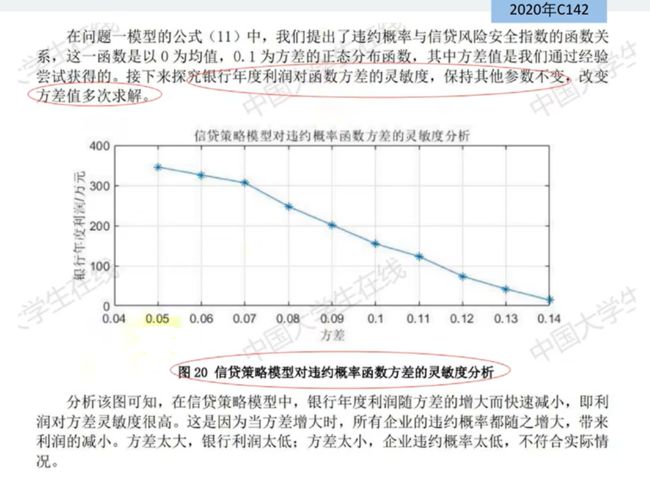
例1(20c)：

针对问题一，主要解决两个问题:

一是需要量化各企业的信贷风险，二是需要给出银行的最优信贷决策。 (方式一)

例2(20b):

针对问题二，本文利用马尔可夫链，建立马尔可夫链天气预测模型，根据第一关的天气转换情况预测其余关

卡的天气情况，再根据问题一的模型得出在不同天气状况下的最佳决策。 (方式二)

例3(20a)：

针对问题二，在大温区温度已知、制程界限给定的前提下确定元件最大过炉速度，实质上是非线性约束条件

下的单目标单变量规划求解问题。 (方式三)

(2) 应用了什么方法?
这里写出你对于这个问题的求解思路，并说明你应用的模型这里写作时一定要紧扣题目本身，不能脱离题目本身来

描述模型。

例1(19e)：

针对问题三，根据问题一和问题二对商场每天的销售额和利润率与打折力度，利用迭代加权最小二乘法，建

立了打折力度为自变量、销售额利润率为因变量的线性回归模型。

例2(19c)：

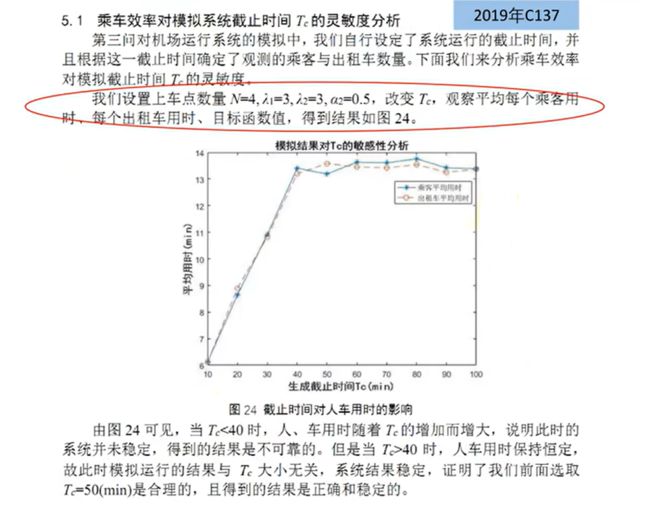
针对上车点的设置问题，需要我们合理安排上车点数量使得机场乘车效率最高。

于是，我们以乘车效率为优化目标，安全因素为约束条件，上车点数量为决策变量，建立单目标优化模型。

其中，我们通过合理制定机场出租车乘车区运行规则，利用计算机模拟的方法，计算得到各方案对应的乘车

效率。

例3(18c)：

针对问题二，本题选用K-均值聚类法，以消费金额和消费次数作为衡量会员购买力的特征数据，运用SPSS 软

件对提取好的数据 (见附录2) 对会员进行聚类，K值以公式 (1) 进行确定。

(3) 得到了什么结果?

在介绍完使用的建模方法后，一定要加上通过这个方法或者模型得到的结果。一般有下面两种情况:

(i) 需要计算出数值答案，例如物理题、规划优化类、预测类直接回答该答案即可。

(如果模型中有重要参数时，我们可以做灵敏度分析(课件后面会介绍什么是灵敏度分析) ;如果涉及概率统计，

可以考虑加上置信区间;如果是预测类或者数值计算类可以考虑加上误差分析)

(i) 开放的问题，例如评价类、提建议类、设计方案策略类对于较为开放的问题，我们在摘要中只需要写出主

要的结论，在下结论时一定要有明确支持的观点，不要模棱两可。

如果有数值描述的结果更好，例如:采取某种建议或者方案后提高了多少、降低了多少。

此外，有时候问题的完整答案很长，这时候只需要在摘要中说出最主要的一部分结果，然后加一句话来引导

读者在正文或者附录中查看完整的结果。

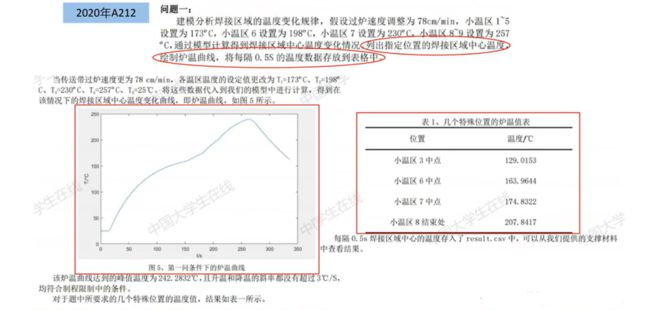
例1 (20a) ：

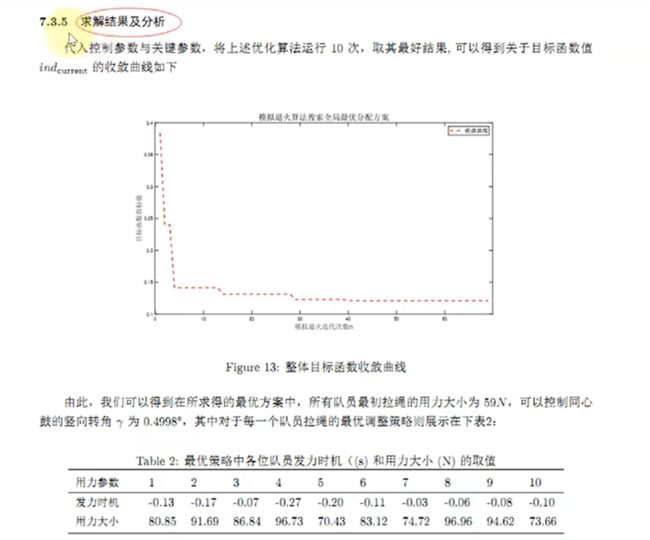
利用模拟退火算法迭代20000次进行求解，得到的最优方案为：

184.2181C(小温区1~5) 、189.8133C(小温区6) 、227.5226C(小温区7)、264.0700C(小温区8~9)

传送带过炉速度为90.0982cm/min.

例2 (20b) ：

使用Matlab和C++编程求解，最终得到:

在最佳策略下，第一关、第二关的剩余资金分别为10470、12730元，并将相应结果填入了Result.xlsx文件;

随后，我们对该模型进行了灵敏度分析。

例3(20c)：

最终获得基于新冠肺炎突发事件下的信贷调整政策，并将其与第二问的结果进行对比，文章发现新冠疫情的

爆发导致银行的信贷策略更加倾向于高新技术产业。

例4(16b)：

求解得到小区开放后，周边一级主路的通行力得分提高了为11.32%，二级主路的通行力得分提高了为

12.89%，三级主路的通行力得分提高了为0.26%。

调整指标之间的直接影响矩阵，发现道路通行力对各指标间相互影响关系的强弱变化比较敏感。

摘要的结尾段

结尾段：

可以总结下全文，也可以介绍下你的论文的亮点也可以对类似的问题进行适当的推广。

(如果写不出来的话可以不写，统计发现只有30%的优秀论文有最后这段)

例1(19d)：(反面教材)

文中所建立的模型简便易行，便于推广，可利用国控点的数据对近邻自建点的数据进行校准。

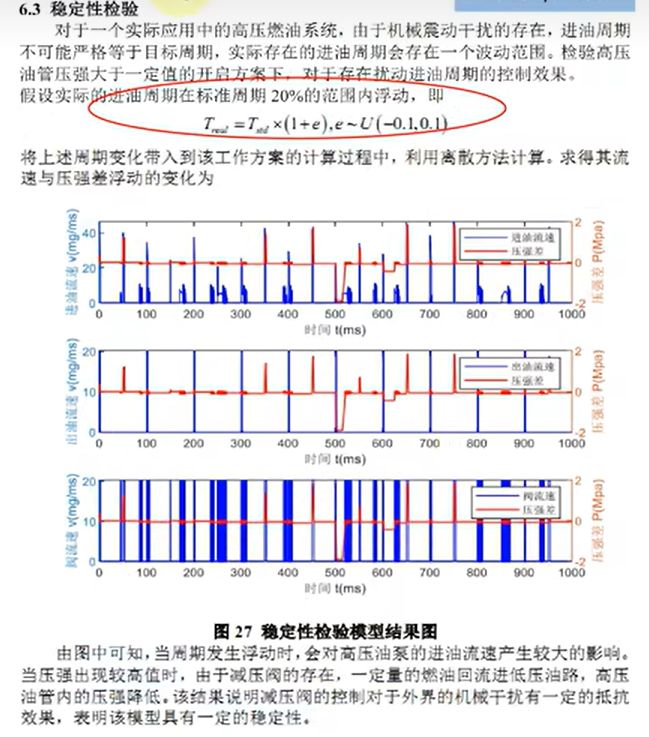
例2(18b)：

本文的亮点在于：首先，利用一般化的公式对系统调度进行了较为细致的机理分析，使得模型具有普适性;

其次，给出了多个调度原则相互比较，从而有利于结果更优;

最后，将蒙特卡洛模拟与机器学习的思想相结合，对上述调度原则的有效性进行验证增强了模型的说服力。

例3(20c)：

最后，本文对模型进行了优、缺点评价与模型推广，信出该模型还可以向银行面对的其他对象和生活的其它

方面进行推广的结论。

例4(20b)：

综上所述，本文依据各题所给的条件较全面地分析了相关因素对玩家决策的影响，并给出了不同条件下玩家

的最佳策略实现了在终点的最大收益。经过分析验证，本文的模型具有合理性和一定的现实意义。

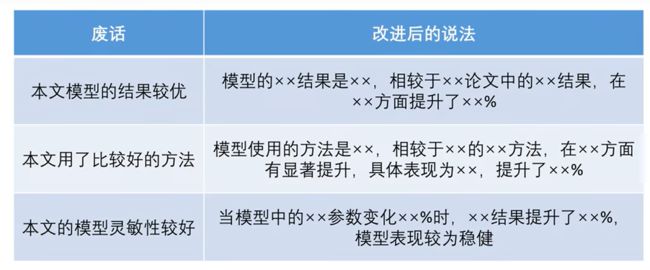
摘要中常见的废话

完整摘要参考

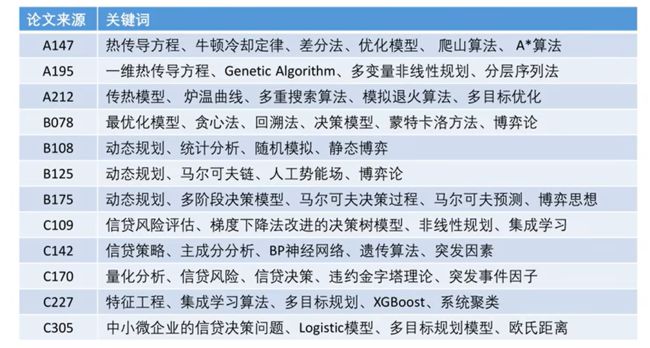
关键词

关键词一般放4-6个，可以放论文中使用的主要模型，也可以放论文里面出现次数较多，能体现论文的主要内容的

词。

（正文部分）

一、问题重述

数学建模比赛论文是要我们解决一道给定的问题，所以正文部分般应从问题重述开始。

一般确定选题后就可以开始。

写这一部分了这部分的内容是将原问题进行整理，将问题背景和题目分开陈述即可。

本部分的目的是要吸引读者读下去，所以文字不可冗长，内容选择不要过于分散、琐碎，措辞要精练。

注意：在写这部分的内容时，绝对不可照抄原题! (论文会查重)

应为：在仔细理解了问题的基础上，用自己的语言重新将问题描述一遍。语言需要简明扼要，没有必要像原题一样

面面俱到。

常规做法: 在原题基础上使用删除替换等方式来重新组织语言。

问题重述案例

二、问题分析

从实际问题到模型建立是一种从具体到抽象的思维过程，问题分析这一部分就是沟通这一过程的桥梁，因为它反映

了建模者对于问题的认识程度如何也体现了解决问题的雏形，起着承上启下的作用，也很能反应出建模者的综合水

平。

这部分的内容应包括：

题目中包含的信息和条件，利用信息和条件对题目做整体分析，确定用什么方法建立模型，一般是每个问题

单独分析一段，分析过程要简明扼要，不需要放结论。

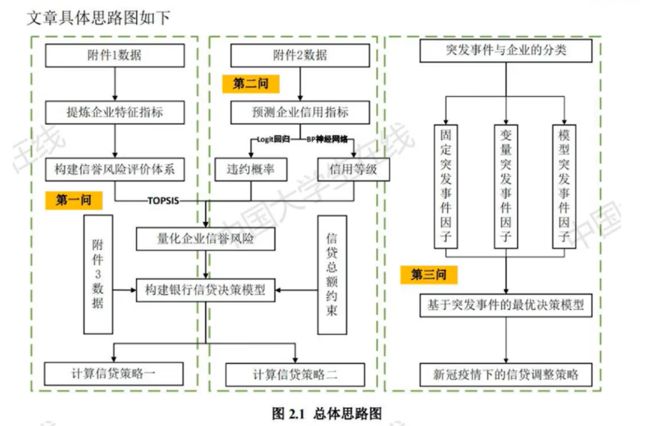
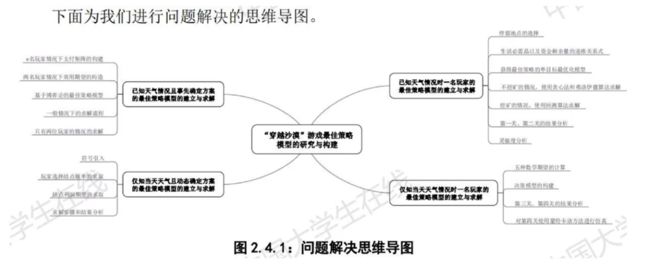
建议在文字说明的同时用图形或图表 (例如流程图)列出思维过程，这会使你的思维显得很清晰，让人觉得一目了然。

一般占据正文不超过一页，题目问题较多时不超过两页。

三、模型假设

模型假设是建立数学模型中非常关键的一步，关系到模型的成败和优劣。所以，应该细致地分析实际问题，从大量

的变量中筛选出最能表现问题本质的变量，并简化它们的关系。由于假设一般不是实际问题直接提供的，它们因建

模人而异，所以在撰写这部分内容时要注意以下几方面:

(1) 论文中的假设要以严格、确切的语言来表达，使读者不致产生任何曲解。

(2)所提出的假设确实是建立数学模型所必需的，包括求解模型所必需的假设和简化模型而做的假设。最终结果与

假设之间会有很强的因果关系，与建立模型无关的假设只会扰乱读者的思考。

(3)假设应验证其合理性。假设的合理性可以从分析问题的过程中得出，例如从问题的性质出发作出合乎常识的假

设；或者由观察所给数据的图像，得到变量的函数形式，也可以参考其他资料类推得到，对于后者应指出参考文献

的相关内容。

模型假设的常见情况

(1) 题目明确给出的假设条件

这种情况最为简单，我们只需要把题目中给我们的假设搬过来就行了。

例如：

2020B题第1问中，题目中假设玩家知道每天天气的状况。

(2) 排除生活中的小概率事件(例如黑天鹅事件、非正常情况)

例如：

交通事故等和交通运输相关的问题中，我们可以假设不存在地质灾难；

和经济金融相关的问题中，我们可以假设不存在经济危机、系统风险等；

和生产制造相关的问题中，我们可以假设不存在设备故障、生产事故等。

(3) 仅考虑问题中的核心因素，不考虑次要因素的影响

(注意: 过于简化的模型会使得你的论文没有优势和亮点)

例如：

考虑传染病的传播规律时，可忽略性别、年龄等因素的影响；

考虑交通拥堵状况时，可只考虑机动车，暂不考虑非机动车和行人；

考虑人口预测问题时，可不考虑移民、大规模人口迁移等因素的影响。

(4) 使用的模型中要求的假设

例如：

使用博弈论模型时可以假设参与博弈者都是“理性人”；

使用Markov模型时可以假设系统或状态具有无后效性；

使用回归模型时可以假设扰动项服从独立的正态分布。

(5) 对模型中的参数形式(或者分布)进行假设

(注意: 如果能在论文中用数据验证这些假设更好)

例如：

假设人口增长服从阻滞增长模型(Logistic模型)；

假设不考虑环境变动时，某鱼群的自然死亡率为常数；

假设产品的寿命(或旅客进机场的时间间隔)服从指数分布；

假设单位时间内排队的人数(或机器出现的故障数)服从泊松分布；

假设生产出来的产品某参数(例如重量、大小)服从N(u,o2)，且各产品独立。

(6) 和题目联系很紧密的一些假设，主要是为了简化模型

这类假设与题目以及建立的模型结合的很紧密，需要我们深入挖掘。

模型假设遇到的问题

(1) 模型假设的合理性怎么保证?

事实上，很少见到有论文来对模型中假设的合理性进行论证，如果需要论证的话可以考虑下面两个角度：

第一：可以引用别人的文献或者资料，这样最有说服力；

第二：如果要对模型中的参数形式(或者分布)进行假设，可以在正文中使用实际数据进行绘图或者进行假设检验来

支持你的假设。

(2) 模型假设设置的太强怎么办?

有同学为了简化问题，往往会给定过强的假设，事实上这样是有一定风险的模型过于简单会显得你的论文没有深度

==和亮点。==如果你建立的模型比别人考虑的因素更多的话，可以在某种程度上看成一种创新。但大多数时候，我们想

考虑的因素或条件也很难进行估算或者考量，这时候你可以在论文后面的模型评价与改进部分加上你的想法，这样

可以在一定程度上弥补这个问题。

四、符号说明

本部分是对模型中使用的重要变量进行说明，一般排版时要放到一张表格中。

注意：

第一：不需要把所有变量都放到这个表里面，模型中用到的临时变量可以不放；

第二：下文中首次出现这些变量时也要进行解释，不然会降低文章的可读性。

五、模型的建立与求解

模型建立：

模型建立是将原问题抽象成用数学语言的表达式，它一定是在先前的问题分析和模型假设的基础上得来的。

因为比赛时间很紧，大多时候我们都是使用别人已经建立好的模型。

这部分一定要将题目问的问题和模型紧密结合起来切忌随意套用模型。

我们还可以对已有模型的某一方面进行改进或者优化，或者建立不同的模型解决同一个问题，这样就是论文的创新

和亮点。

模型求解：

把实际问题归结为一定的数学模型后，就要利用数学模型求解所提出的实际问题了。

一般需要借助计算机软件进行求解，例如常用的软件有MatlabSpss, Lingo, Excel, Stata, Python等。

求解完成后，得到的求解结果应该规范准确并目醒目，若求解结果过长，最好编入附录里。

(注意: 如果使用智能优化算法或者数值计算方法求解的话，需要简要阐明算法的计算步骤)

布局：

模型求解的注意事项

(1) 国赛中常出优化类问题，如果你用到了启发式算法求解的话，一定要简要写明算法步骤，并要结合具体的问题来阐明计算的思路。

(2) 求解的结果应该在论文中突出的展示出来，有具体答案的问题比较简单直接放上数值计算结果即可；

如果是开放类问题的话，一定要对结果进行阐明和解释，如果能加上美观整洁的图表就更好了。

六、模型的分析与检验（模型检验）

模型的分析与检验的内容也可以放到模型的建立与求解部分，这里我们单独抽出来进行讲解，因为这部分往往是论文的加分项，很多优秀论文也会单独抽出一节来对这个内容进行讨论。

模型的分析 :

在建模比赛中模型分析主要有两种，一个是灵敏度(性)分析另一个是误差分析。

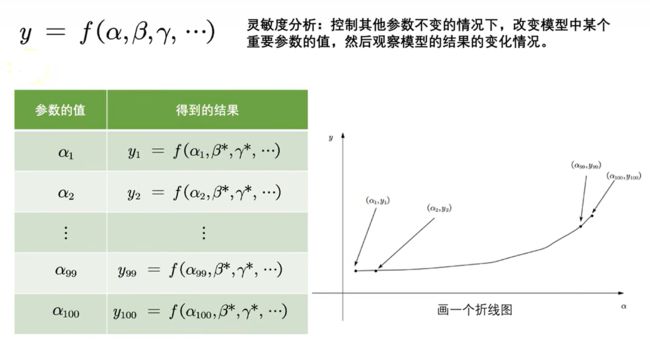
灵敏度分析是研究与分析一个系统 (或模型)的状态或输出变化对系统参数或周围条件变化的敏感程度的方法。

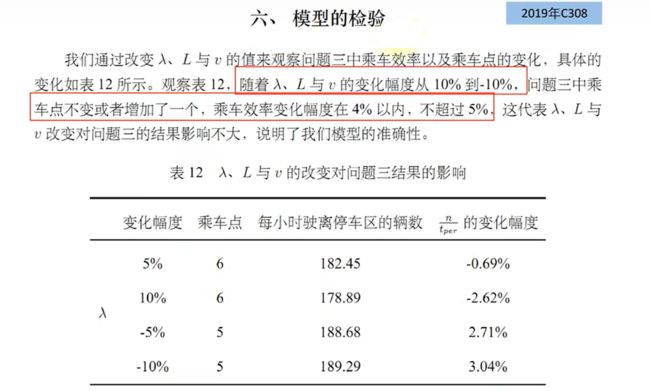
其通用的步骤是: 控制其他参数不变的情况下，改变模型中某个重要参数的值，然后观察模型的结果的变化情况。

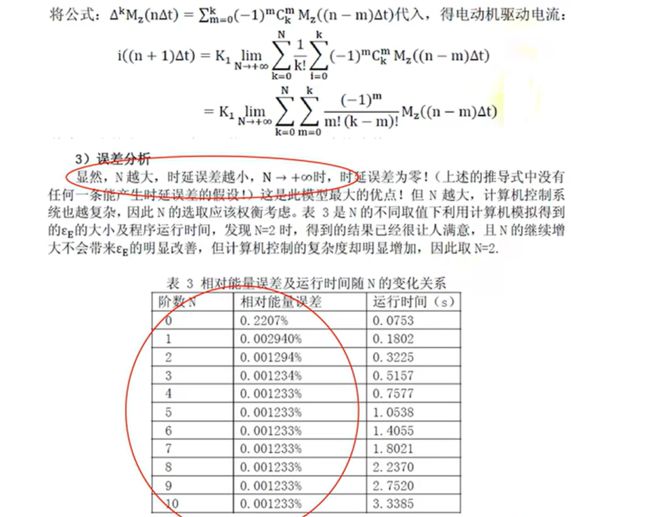
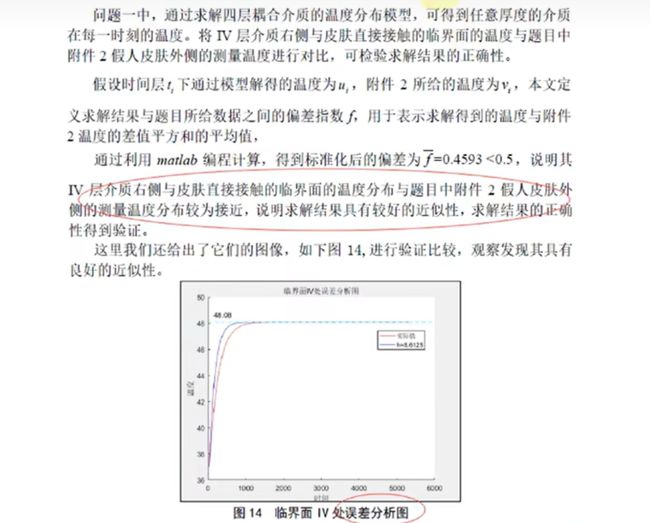
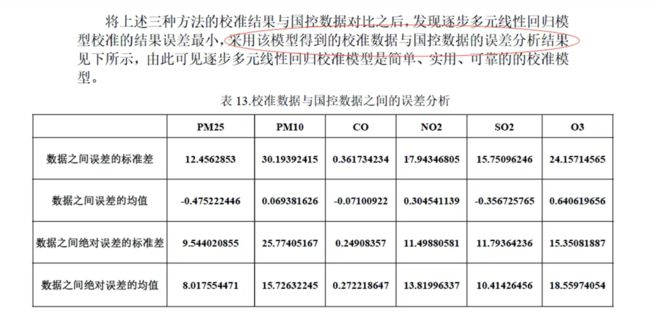
误差分析是指分析模型中的误差来源，或者估算模型中存在的误差，一般用于预测问题或者数值计算类问题。

模型的检验：

模型检验可以分为两种：

一种是使用模型之前应该进行的检验，例如层次分析法中一致性检验，灰色预测中的准指数规律的检验，这部分内

容应该放在模型的建立部分；

另一种是使用了模型后对模型的结果进行检验数模中最常见的是稳定性检验，实际上这里的稳定性检验和前面的灵

敏度分析非常类似。

灵敏度分析

灵敏度分析参考实例

稳定性检验

误差分析

---

---

---

七、模型的评价、改进与推广

本部分的标题需要根据你的内容进行调整，

例如: 如果你没有写模型推广的话，就直接把标题写成模型的评价与改进。

很多论文也把这部分的内容直接统称为“模型评价”部分。

三个部分写什么内容?

模型的评价：主要写模型的优缺点；

模型的改进：主要是针对模型中缺点有哪些可以改进的地方；

模型的推广：将原题的要求进行扩展，进一步讨论模型的实用性和可行性。

其中，优缺点是必须要写的内容下面两个内容是可选的，但还是建议大家写，实力比较强的建模者可以在这

一块充分发挥，这部分对于整个论文的作用在于画龙点睛。

---

---

---

八、参考文献

注意事项：

(1) 引用的内容需要在正文中标注出来

(2) 不要引用别人的博客

(3) 不能引用前辈们论文里面的内容

附录

论文附录内容应包括支撑材料的文件列表，建模所用到的全部完整、可运行的源程序代码 (含EXCEL、SPSS等软件的交互命令) 等。

如果缺少必要的源程序程序不能运行或运行结果与论文不符，都可能会被取消评奖资格。

如果确实没有用到程序，应在论文附录中明确说明“本论文没有用到程序”。

支撑材料内容包括用于支撑模型、结果、结论的所有必要材料，至少应包含建模所用到的所有可运行源程序、自主

查阅使用的数据资料(赛题中提供的原始数据除外) 、较大篇幅中间结果的图表等。

将所有支撑材料文件使用WinRAR软件压缩在一个文件中 (后缀为RAR或ZIP，大小不超过20MB) 。

支撑材料的文件列表应放入论文附录；

如果确实没有需要提供的支撑材料，可以不提供支撑材料文件，并在论文附录中注明“本论文没有支撑材料”。

如果支撑材料文件与论文内容不相符，该论文可能会被取消评奖资格。

注意竞赛的承诺书和编号专用页不要放在支撑材料中，所有文件中不能有显示参赛者身份和所在学校及赛区的信息。

美赛

通用框架：

Summary Sheet（摘要页）

摘要

Title & Keywords（标题和关键词）

Keywords 指的是关键词，因为有些英文词组很长，美赛中关键词一般放3-6个，也有的论文干脆不写关键词。

关键词可以放你的模型或者和文章内容结合紧密的词。

Content（目录）

1.Introduction

Introduction可以翻译成引言部分，大部分特等奖论文的引言部分都包含两到三个小部分。

我在下面给出了常见的四个小部分，大家可以根据自己的需要保留你要写的部分。

1.Problem Background(问题背景)

这个小部分里面可以总结题目所给问题的背景，也可以加上自己查到的一些相关的资料，不要直接照搬题目。

小技巧:美赛的问题比国赛要更开放，大家写这个部分时可以结合你对于赛题的理解，要将这个背景介绍有侧重的

往自己研究的方向去靠。

例如，某个现实问题往往会涉及到经济、社会、生态、文化等各个层面，如果你的模型主要针对该问题对经济造成

的影响，那么你的背景介绍就侧重于对经济层面的影响来写。

2.Restatement of the Problem

注意：记得改一下，防止查重。

3.Literature Review

文献综述参考实例：

总结写作特点:

有很多学者都研究过这个问题(红色圈出来的编号就是参考文献的标记)，其中:

• 某某学者建立了某某模型或者使用了某某方法研究了这个问题；
• 某某学者通过研究了这个问题得到了某某结论。

技巧: 文献综述中的文章能直接和你的论文中使用的模型或者得到的结论相互呼应。

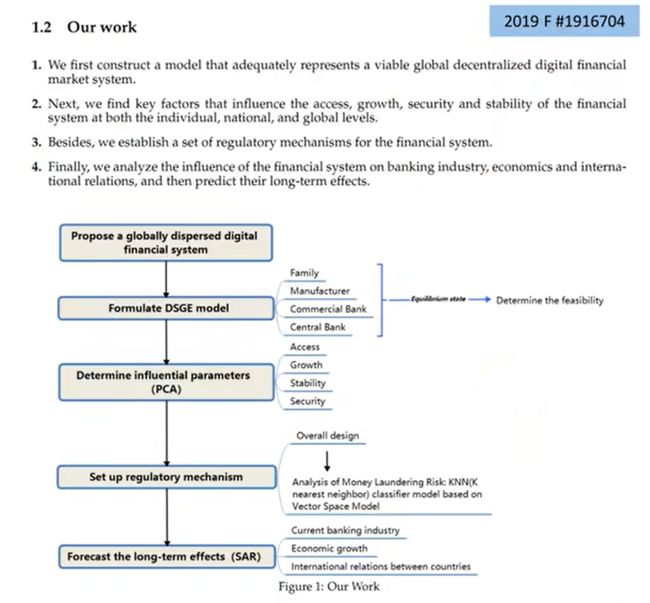
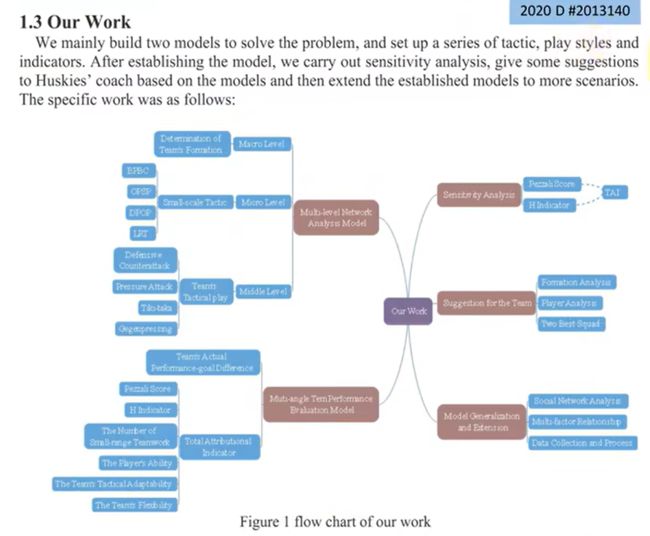
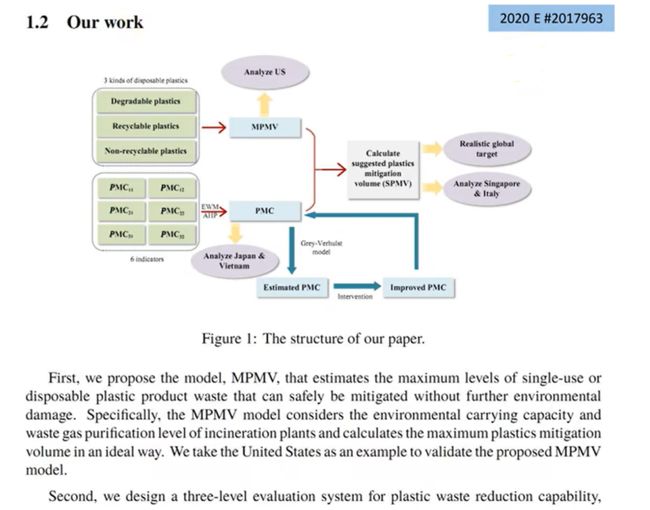
4.Our Work

---

---

---

2. Assumptions and Justifications

---

3. Notations

4&5&6. The name of model 1,2,3

以模型的名称命名，美赛中这种写法比较常见。

Data Description部分 (不常见)

7. Sensitivity Analysis（非常重要！！！）

8.Model Evaluation and Further Discussion

9.Conclusion

---

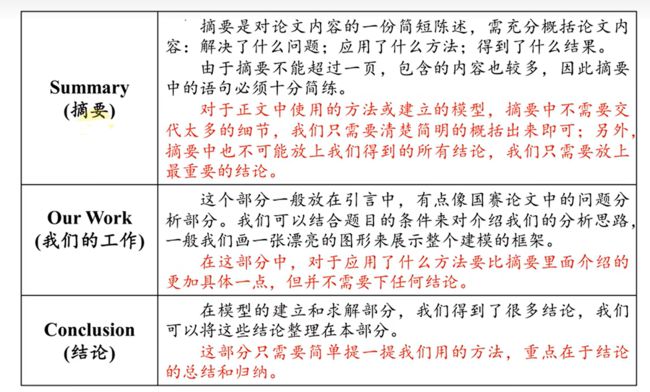
三个部分的区别

References（参考文献）

Appendices（附录）

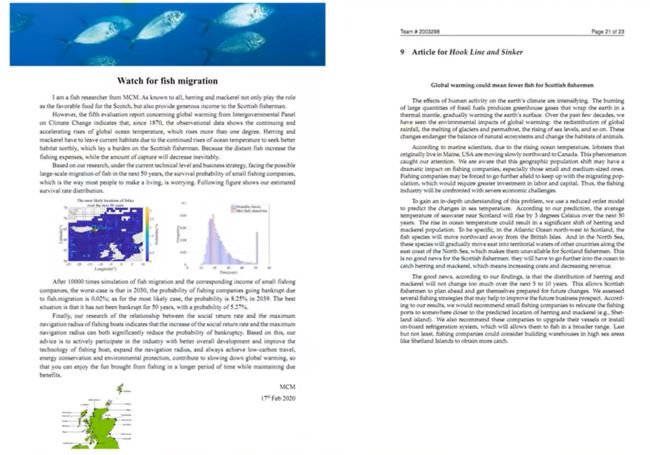
Article

美赛有些题目会要求大家给某个杂志写一篇文章(Article)，例如：

参考实例：

Letter

美赛有些题目会要求大家写一封信(Letter)，例如：

Memo

美赛有些题目会要求大家写一份备忘录(Memo)，例如：