Numpy中的矩阵乘法

numpy中对于矩阵乘法运算有以下几种： * , dot, vdot, inner, matmul

对于array和matrix对象使用上述运算的时候效果存在不同

对于array对象而言

* 相当于matlab中的*，即数组中对应位置上元素相乘

dot

numpy.dot(a, b, out=None)

• 如果a和b都是一维数组，则等价于inner，向量内积
• 如果a和b都是二维数组，为矩阵乘法，等价于matmul 和 @，但更推荐使用matmul或者@
• 如果a或者b有一个是标量，为按对应元素相乘，等价于multiply和*，但是更推荐使用multiply或*
• 如果a是N维数组，b是一维数组，它是a和b在最后一个轴上的和积（ sum product，这啥？）
• 如果a是N维数组，b是M维数组，M大于等于2，则为沿a最后一个轴和沿b倒数第二个轴的sum product

sum product： 

dot(a, b)[i,j,k,m] = sum(a[i,j,:] * b[k,:,m])

>>> a = np.arange(3*4*5*6).reshape((3,4,5,6))
>>> b = np.arange(3*4*5*6)[::-1].reshape((5,4,6,3))
>>> np.dot(a, b)[2,3,2,1,2,2]
499128
>>> sum(a[2,3,2,:] * b[1,2,:,2])
499128

https://docs.scipy.org/doc/numpy/reference/generated/numpy.dot.html?highlight=dot#numpy.dot

 

vdot 

返回两个向量的点乘

vdot(a, b)函数处理复数的方式与(a, b)不同，如果第一个参数是复数，则使用第一个参数的复共轭来计算点积

注意，vdot处理多维数组的方式与dot不同:它不执行矩阵乘积，而是首先将输入参数平摊为一维向量。因此，它只能用于向量。

>>> a = np.array([1+2j,3+4j])
>>> b = np.array([5+6j,7+8j])
>>> np.vdot(a, b)
(70-8j)
>>> np.vdot(b, a)
(70+8j)

注意：高维数组被摊成了一维：

>>> a = np.array([[1, 4], [5, 6]])
>>> b = np.array([[4, 1], [2, 2]])
>>> np.vdot(a, b)
30
>>> np.vdot(b, a)
30
>>> 1*4 + 4*1 + 5*2 + 6*2
30

https://docs.scipy.org/doc/numpy/reference/generated/numpy.vdot.html#numpy.vdot

inner 数组内积

numpy.inner(a, b)

一维数组向量的普通内积(不含复共轭)

对于高维数组，为沿最后一个轴的和积

https://docs.scipy.org/doc/numpy/reference/generated/numpy.inner.html?highlight=inner#numpy.inner

import numpy as np 
import numpy.matlib
a = np.array([[1,2],[3,4]])
b = np.array([[5,6],[7,8]])
print('矩阵a：')
print(a)
print('矩阵b:')
print(b)
print('-------------------------------')
c = a*b
print(c)
print('-------------------------------')
d = np.dot(a,b)
print(d)
print('-------------------------------')
e = np.matmul(a,b)
print(e)
print('-------------------------------')
f = np.vdot(a,b)
print(f)
print('-------------------------------')
g = np.inner(a,b)
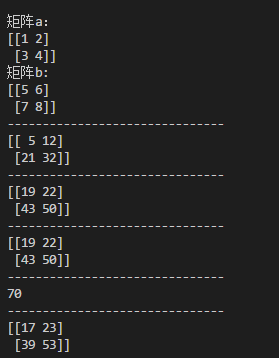
print(g)

输出如下

另外，在一维情形下，dot和vdot似乎等价

import numpy as np 
a = np.array([1,2,3,4])
b = np.array([1,2,3,4])
print(np.dot(a,b))
print(np.vdot(a,b))

输出均为

对于matrix对象，*为矩阵乘法，和dot，matmul等价，使用multiply进行对应元素相乘

import numpy as np 
a = np.mat('1,2;3,4')
b = np.mat('1,2;3,4')
print('矩阵a')
print(a)
print('矩阵b')
print(b)
print('-----------------------------')
print(a*b)
print('-----------------------------')
print(np.dot(a,b))
print('-----------------------------')
print(np.matmul(a,b))
print('-----------------------------')
print(np.multiply(a,b))

输出