深度学习_Python_TensorFlow之卷积神经网络

本文准备以MNIST数据集为案例，使用Python语言和TensorFlow平台构建卷积神经网络模型。

一、准备工作

• 具备一定的Python语言基础知识，安装任何可用的Python开发工具，安装TensorFlow库，使用pip库安装

pip install tensorflow

然后在解释器中导入tensorflow库（import tensorflow），看是否有错，没有，则安装成功。

• 下载MNIST数据集，了解该数据集的内容。这块可用看看Tensorflow官方文档中文版，链接：http://www.tensorfly.cn/tfdoc/tutorials/mnist_beginners.html

二、卷积神经网络

深层的神经网络与最常见的单一隐藏层神经网络的区别在于深度。深度神经网络中，每一个节点层在前一层输出的基础上学习识别一组特定的特征，随着神经网络深度的增加，节点所能识别的特征也越来越复杂。

对于常见的全连接神经网络来说，存在以下几点不足：

• 参数太多，在MNIST数据集中，只有28*28*1，就会有这么多权重，如果说更大的图片，比如200*200*3，就需要120000多个，这完全是浪费；
• 没有利用像素之间位置信息，对于图像识别任务来说，每个像素与周围像素的联系都是比较紧密的；
• 层数限制，准确度不会因为层数的增加而无上限的提高。

而卷积神经网络拥有着卷积层和池化层组合在一起的特征提取器，它权重共享的机制解决了权重爆炸的问题，这种特定结构的神经网络模型受到了大家的青睐。

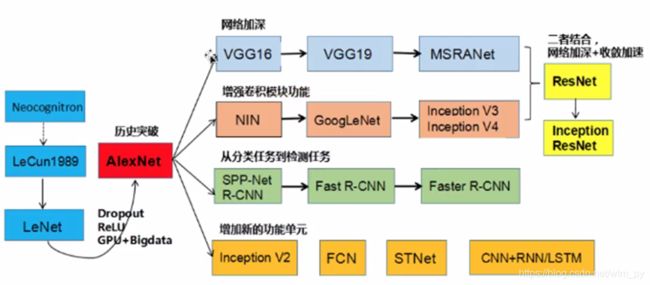
下图是卷积神经网络的错误率、发展历史和方向：

神经网络（Neural Network）的基本组成包括输入层、隐藏层和输出层。而卷积神经网络的特点在于隐藏层分为卷积层（convolution layer）和池化层（pooling layer，又叫下采样层）

网络中的数据变化如下所示，可以看出，卷积神经网络的数据的宽度和高度会不断减小，但深度会不断提高

卷积神经网络结构分析：

1.卷积层

• 卷积层过滤器（卷积核）：

个数；大小（一般为1*1、3*3、5*5）；步长（一般为1）；零填充（‘SAME’或‘VALID’）

卷积层的输出深度由过滤器个数决定，输出宽度和高度用如下公式进行计算

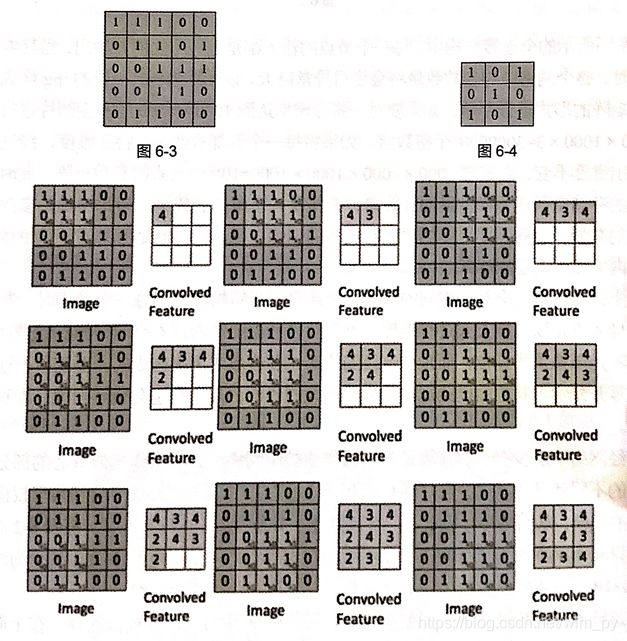
卷积层计算过程示意图如下：

上图是不填充0的卷积方式，根据公式H2 = (5 - 3 + 2*0)/1+1 = 3，填充0时输出宽度和高度等于输入的宽度和高度，根据公式可放推出零填充的大小为1，我们只需要选择参数padding是'SAME'（越过边缘取样）还是'VALID'（不越过边缘取样），具体大小不需要知道。

• 卷积操作API

tf.nn.conv2d(input,filter,strides=,padding=,name=None)

其中：

• input：给定的输入张量，[batch,height,width,channel]，类型为float32,64

• filter：指定过滤器的大小，[filter_height,filter_width,in_channels,out_channels]

• strides：步长，strides=[1,stride,stride,1]

• padding：'SAME'或'VALID'

 

2.激活函数

把线性关系转换为非线性关系的函数，叫做激活函数（activation function），作用是增加网络的非线性分割能力。

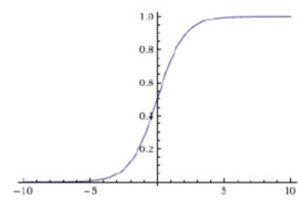
一般使用的激活函数有：Sigmoid、Tanh和Relu，他们的公式和图示如下：

• Sigmoid

• Tanh

• Relu

前人经验证明，Relu函数是更优选择，理由是：

• 采用sigmoid等函数，反向传播求误差梯度时，计算量相当大，而采用relu激活函数，整个过程的计算量节省很多

• 对于深层网络，sigmoid函数反向传播时，很容易就会出现梯度爆炸的情况

Relu激活函数API：

tf.nn.relu(features,name=None)

其中：features表示卷积操作后加上偏置项后的结果

 

3.池化层

Pooling层主要的作用特征提取，通过去掉Feature Map中不重要的样本，进一步减少参数数量。Pooling的方法很多，最常用的是Max Pooling。2*2大小，2步长。

最大池化的操作示意图如下：

池化函数API：

tf.nn.max_pool(value,ksize=,strides=,padding=,name=None)

• value：Tensor的形态：[batch,height,width,channels]
• ksize：池化窗口大小，[1,ksize,ksize,1]
• strides：步长大小，[1,stride,stride,1]
• padding：'SAME'或'VALID'

 

4.全连接层

前面的卷积和池化相当于做特征工程，后面的全连接相当于特征加权。最后的全连接层在整个卷积神经网络中起到“分类器”的作用。

全连接层之间做矩阵乘法

 

三、卷积神经网络Python代码编写

1.网络设计

这里我们暂且把卷积、激活、池化泛称为一卷积层，重点是明白数据形态在网络中的变化，理清思路，这对后续的程序编写很有好处。

根据上面的模型设计图，参照之前介绍的API，模型的程序如下：

#定义一个定义初始化权重的函数
def weight_variable(shape):
	w = tf.Variable(tf.truncated_normal(shape,mean=0.0,stddev=0.1))
	return w

#定义一个初始化偏置的函数
def bias_variable(shape):
	b = tf.Variable(tf.constant(0.1,shape=shape))
	return b

def model():
	"""
	自定义卷积模型
	"""
	#准备数据的占位符x:[None,784]; yTrain:[None,10]
	x = tf.placeholder(tf.float32,[None, 784])
	#对x的形态进行改变：[None,784]----->[None,28,28,1]
	x_reshape = tf.reshape(x,[-1,28,28,1])
	#目标值
	yTrain = tf.placeholder(tf.float32,[None, 10])

	#一层卷积，卷积:[5*5*1],32个，strides=1；激活：tf.nn.relu；池化
	w_conv1 = weight_variable([5,5,1,32])  #filter1
	b_conv1 = bias_variable([32])

	#卷积操作+激活函数; 形态：[None,28,28,1]----->[None,28,28,32]
	x_relu1 = tf.nn.relu(tf.nn.conv2d(x_reshape,w_conv1,strides=[1,1,1,1],padding='SAME') + b_conv1)

	#池化：2*2大小，strides=2; 形态:[None,28,28,32]----->[None,14,14,32]
	x_pool1 = tf.nn.max_pool(x_relu1,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')

	#二层卷积:5*5*32,64个,strides=1;激活:tf.nn.relu;池化
	w_conv2 = weight_variable([5,5,32,64])  #filter2
	b_conv2 = bias_variable([64])

	#卷积、激活、池化操作
	#形态：[None,14,14,32]----->[None,14,14,64]
	x_relu2 = tf.nn.relu(tf.nn.conv2d(x_pool1,w_conv2,strides=[1,1,1,1],padding='SAME') + b_conv2)
	#池化：2*2大小，strides=2; 形态:[None,14,14,64]----->[None,7,7,64]
	x_pool2 = tf.nn.max_pool(x_relu2,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')

	#全连接层：[None,7,7,64]----->[None,7*7*64] * [7*7*64,10]----->[None,10]
	w_fc = weight_variable([7*7*64,10])
	b_fc = bias_variable([10])

	#改变形态
	x_pool2_flat = tf.reshape(x_pool2,[-1,7*7*64])

	y_predict = tf.nn.softmax(tf.matmul(x_pool2_flat,w_fc) + b_fc)

	return x,yTrain,y_predict

四、MNIST数据集手写图片识别卷积神经网络完整代码及展望

了解了卷积神经网络如何编写代码后，加入读取数据、计算交叉熵、计算准确率、优化器、初始化、定义会话、开始训练等环节就可写出完整代码，我们有又加入了一层全连接层和dropout层使网络更加合理

完整代码如下：

import tensorflow as tf
import numpy as np
import pandas as pd
import input_data

#定义一个定义初始化权重的函数
def weight_variable(shape):
	w = tf.Variable(tf.truncated_normal(shape,mean=0.0,stddev=0.1))
	return w

#定义一个初始化偏置的函数
def bias_variable(shape):
	b = tf.Variable(tf.constant(0.1,shape=shape))
	return b

def model():
	"""
	自定义卷积模型
	"""
	#准备数据的占位符x:[None,784]; yTrain:[None,10]
	x = tf.placeholder(tf.float32,[None, 784])
	#对x的形态进行改变：[None,784]----->[None,28,28,1]
	x_reshape = tf.reshape(x,[-1,28,28,1])
	#目标值
	yTrain = tf.placeholder(tf.float32,[None, 10])

	#一层卷积，卷积:[5*5*1],32个，strides=1；激活：tf.nn.relu；池化
	w_conv1 = weight_variable([5,5,1,32])  #filter1
	b_conv1 = bias_variable([32])

	#卷积操作+激活函数; 形态：[None,28,28,1]----->[None,28,28,32]
	x_relu1 = tf.nn.relu(tf.nn.conv2d(x_reshape,w_conv1,strides=[1,1,1,1],padding='SAME') + b_conv1)

	#池化：2*2大小，strides=2; 形态:[None,28,28,32]----->[None,14,14,32]
	x_pool1 = tf.nn.max_pool(x_relu1,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')

	#二层卷积:5*5*32,64个,strides=1;激活:tf.nn.relu;池化
	w_conv2 = weight_variable([5,5,32,64])  #filter2
	b_conv2 = bias_variable([64])

	#卷积、激活、池化操作
	#形态：[None,14,14,32]----->[None,14,14,64]
	x_relu2 = tf.nn.relu(tf.nn.conv2d(x_pool1,w_conv2,strides=[1,1,1,1],padding='SAME') + b_conv2)
	#池化：2*2大小，strides=2; 形态:[None,14,14,64]----->[None,7,7,64]
	x_pool2 = tf.nn.max_pool(x_relu2,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')

	#全连接层1：[None,7,7,64]----->[None,7*7*64] * [7*7*64,1024]----->[None,1024]
	w_fc1 = weight_variable([7*7*64,1024])
	b_fc1 = bias_variable([1024])

	#改变形态
	x_pool2_flat = tf.reshape(x_pool2,[-1,7*7*64])

	x_fc1 = tf.nn.relu(tf.matmul(x_pool2_flat,w_fc1) + b_fc1)

	#dropout层，防止过拟合
	x_fc1_drop = tf.nn.dropout(x_fc1,keep_prob)

	#输出层：[None,1024] * [1024,10]----->[None,10]
	w_fc2 = weight_variable([1024,10])
	b_fc2 = bias_variable([10])

	y_predict = tf.nn.softmax(tf.matmul(x_fc1_drop,w_fc2) + b_fc2)
	return x,yTrain,y_predict

#获取数据
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
sess = tf.InteractiveSession()

#打印数据条数
print("training data:",mnist.train.num_examples)
print("testing data:",mnist.test.num_examples)

#dropout,减少过拟合，
keep_prob = tf.placeholder('float')

x,yTrain,y_predict = model()

#计算交叉熵
cross_entropy = -tf.reduce_sum(yTrain * tf.log(y_predict))  # 交叉嫡，cost function

# 使用优化器来降低cost，学习速率为1e-4,以交叉熵最小原则
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)

#计算准确率
correct_prediction = tf.equal(tf.argmax(y_predict, 1), tf.argmax(yTrain, 1))  #找出预测正确的标签
accuracy = tf.reduce_mean(tf.cast(correct_prediction, 'float'))  #把布尔值换成浮点数

# 初始化已经创建的变量
sess.run(tf.global_variables_initializer())

# 训练模型，运行n次，每次随机抽取50个
for i in range(10000):
	batch= mnist.train.next_batch(50)
	if i%100 == 0:
		train_accuracy = accuracy.eval(feed_dict={x:batch[0],yTrain:batch[1],keep_prob:1})
		print ("step %d, train accuracy %g"%(i, train_accuracy))
	train_step.run(feed_dict={x:batch[0],yTrain:batch[1],keep_prob:0.5})
print("test accuracy %g"%accuracy.eval(feed_dict={x:mnist.test.images,yTrain:mnist.test.labels,keep_prob:1.0}))

运行10000次后，结果如下

测试集精度达到了99.08%。

使用卷积神经网络实现MNIST手写图片识别，根据网络资料（https://www.cnblogs.com/bonelee/p/8528863.html），不断优化网络后，实验精度变化如下表：

卷积神经网络结构	验证数据集精度
一个卷积层	98.78%
两个卷积层	99.06%
两个卷积层+线性修正单元ReLU+正则化	99.23%
两个卷积层+线性修正单元ReLU+正则化+拓展数据集	99.37%
两个卷积层+线性修正单元ReLU+正则化+拓展数据集+继续插入格外的全连接层	99.43%
两个卷积层+线性修正单元ReLU+正则化+拓展数据集+继续插入格外的全连接层+弃权技术	99.60%
个卷积层+线性修正单元ReLU+正则化+拓展数据集+继续插入格外的全连接层+弃权技术+组合网络	99.67%

小型的卷积神经网络我们可以按照本文步骤进行设计编程，但是要是有几十层、上百层的网络呢？

推荐可以使用GoogleNet等卷积神经网络框架来实现。只需要知道很少的内容（如原始输入图像的规格等），不需要了解具体细节就可以。

后续的学习可以多找些实例来练习设计卷积神经网络并编写代码，之后学习GoogLeNet等框架。