二叉树后序遍历（递归法和迭代法(非递归法)）——C++

 声明：本文原题主要来自力扣，记录此博客主要是为自己学习总结，不做任何商业等活动！

二叉树的遍历有前序遍历、中序遍历、后序遍历和层次遍历，其中二叉树基本知识点可以参考博主上篇博客（二叉树基本知识点图文介绍(全网最简洁)），二叉树的前序遍历可以参考博主这篇博客（二叉树前序遍历(递归法和迭代法(即非递归法))——C++），中序遍历可以参考博主这篇博客（二叉树中序遍历（递归法和迭代法(非递归法)）——C++），本文主要总结二叉树的后续遍历。

一、二叉树后序遍历

后序遍历是先遍历左子节点left，在遍历右子节点right，最后遍历父节点parent，即遍历顺序：

left ——> right ——> parent

下面是力扣原题，写一个后序遍历程序。

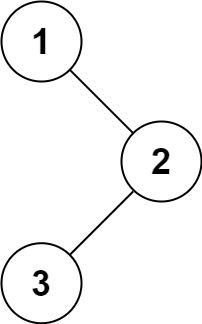
给定一个二叉树的根节点 root ，返回它的后序遍历。

示例 1：

​

输入：root = [1,null,2,3]
输出：[1,3,2]

1.1 递归法

递归法主要用编译器栈自动压入递归的函数参数和局部变量，依次按照后序遍历顺序有且仅有一次访问二叉树。下面是具体示例代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector postorderTraversal(TreeNode* root) {
        if(root == nullptr)
            return datas;
        if(root->left != nullptr)
            postorderTraversal(root->left);
        if(root->right != nullptr)
            postorderTraversal(root->right);
        datas.push_back(root->val);
        return datas;
    }
private:
    vector datas;
};

结果：

​

  1.2 迭代法

由于后续遍历如果按照正常迭代思路去实现将不好理解和实现，仔细观察下面前序和后续遍历顺序，可以发现一个规律：

1. 前序遍历： parent ——> left ——> right
2. 前序遍历：  left ——> right ——> parent，
3. 将后续遍历逆序过来遍历，则：parent ——> right ——> left

通过观察1和3可以发现，两者都是先遍历父节点，再遍历左右子节点，这种遍历方式在迭代法中容易用代码实现，故可以先按照后序遍历的相反顺序遍历二叉树节点，最后将遍历的结果数组逆转一下即可。

1.2.1 具体实现步骤

a1 将父节点压入栈

if (root == nullptr)
return datas;
TreeNode* cur = root;
std::stack nodeStack;
nodeStack.push(cur);

a2 访问父节点，然后将左子节点压栈，最后右子节点压栈

这样做的目的是为了弹出栈的时候先遍历父节点，再遍历右子节点，最后遍历左子节点。

cur = nodeStack.top();
nodeStack.pop();
datas.push_back(cur->val);
if (cur->left != nullptr)
nodeStack.push(cur->left);
if (cur->right != nullptr)
nodeStack.push(cur->right);

a3 循环步骤a1和a2，直到整个栈为空结束循环

while (!nodeStack.empty())
{
    cur = nodeStack.top();
    nodeStack.pop();
    datas.push_back(cur->val);
    if (cur->left != nullptr)
        nodeStack.push(cur->left);
    if (cur->right != nullptr)
        nodeStack.push(cur->right);
}

a4 逆转遍历的结果数组即可

std::reverse(datas.begin(), datas.end());

1.2.2完整代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector postorderTraversal(TreeNode* root) {
        if(root == nullptr)
            return datas;
        TreeNode* cur = root;
        std::stack nodeStack;
        nodeStack.push(cur);
        while(!nodeStack.empty())
        {
            cur = nodeStack.top();
            nodeStack.pop();
            datas.push_back(cur->val);
            if(cur->left != nullptr)
                nodeStack.push(cur->left);
            if(cur->right != nullptr)
                nodeStack.push(cur->right);
        }
        std::reverse(datas.begin(), datas.end());        
        return datas;
    }
private:
    vector datas;
};

结果：

1.3总结

由上面迭代法实现后序遍历跟前序遍历迭代法几乎一样，只是变化了一个左右节点访问顺序和多了一个逆转遍历结果数组步骤。前序遍历可以参考博主这篇博客（二叉树前序遍历(递归法和迭代法(即非递归法))——C++）。

通过后序遍历取巧用法我们可以思考遇到类似的问题时，多角度思考一下，是否可以通过将问题变化一个角度进行解题，比如逆转，旋转等方法与现有的容易实现的方法比对，这样可以极大提高效率和解决问题。