LeNet模型详解以及代码实现

一、卷积神经网络的构成

输入层

整个网络的输入，一般代表了一张图片的像素矩阵。上图中最左侧三维矩阵代表一张输入的图片，三维矩阵的长、宽代表了图像的大小，而三维矩阵的深度代表了图像的色彩通道（channel）。黑白图片的深度为 1，RGB 色彩模式下，图片的深度为 3。

卷积层

CNN 中最为重要的部分。与全连接层不同，卷积层中每一个节点的输入只是上一层神经网络中的一小块，这个小块常用的大小有 3×3 或者 5×5。一般来说，通过卷积层处理过的节点矩阵会变的更深。
卷积层的计算：
在这个卷积层，有两个关键操作：
（1）局部关联：每个神经元看做一个滤波器(filter)
（2）窗口(receptive field)滑动： filter对局部数据计算
先介绍卷积层中遇到的几个名词：
深度（depth）：如下图所示

步长（stride）：滑动窗口每次移动的长度
填充值（padding）：
举个例子，有一个5 * 5的图片，我们滑动窗口为2 * 2，步长取2，发现还有一个像素没法滑动，如下图。

我们可以在原有的矩阵填充一层，使其变成6 * 6的矩阵，如下图，这时滑动窗口就可以把所有像素遍历完。

卷积操作:

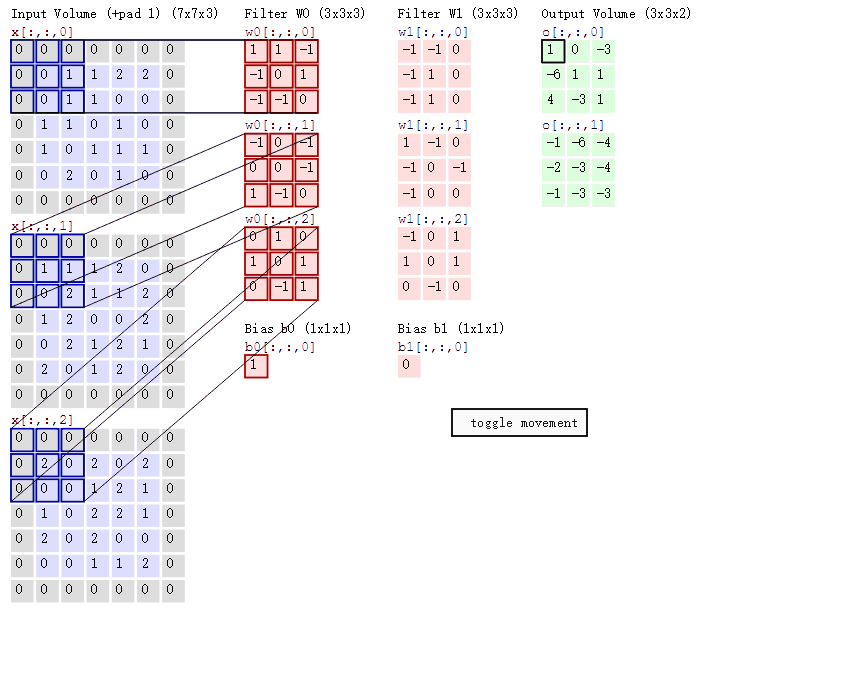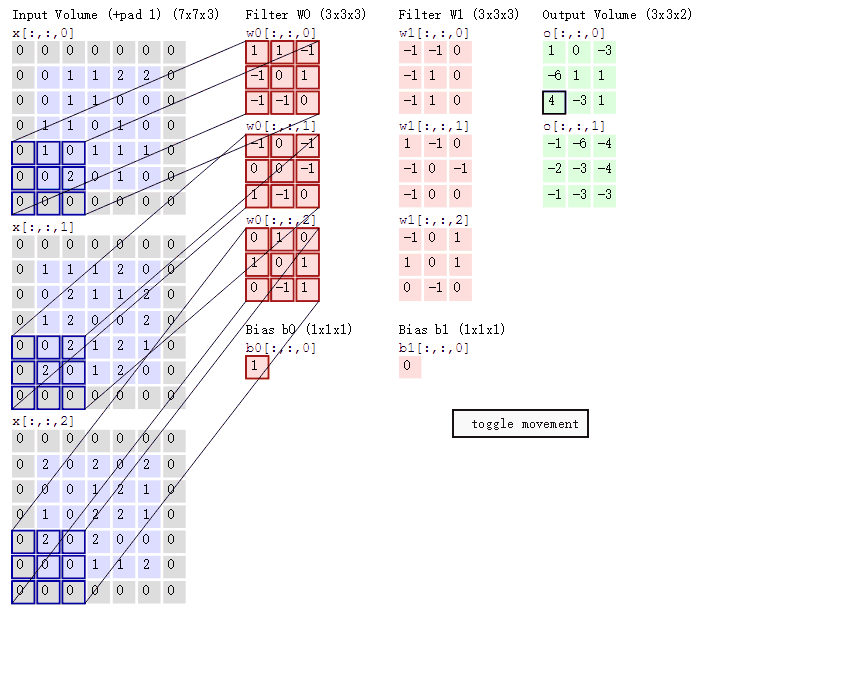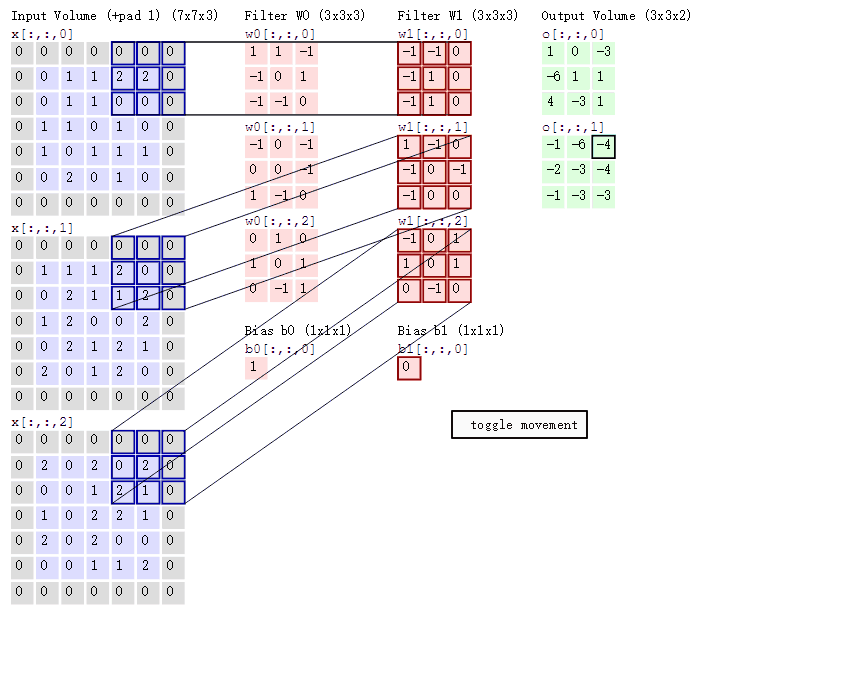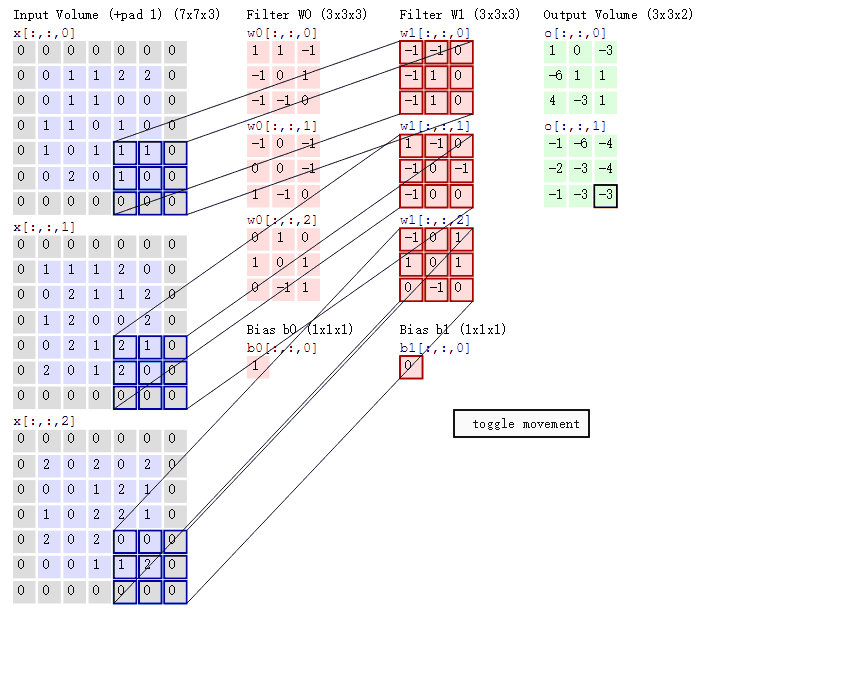
特征图的边长公式为：$N=(W-F+2P)/S+1$
其中，W是输入的图像，F是卷积核大小，P是填充值，S是步长。

激活函数

-激活函数层的作用是协助卷积层表达复杂的特征。卷积神经网络通常使用线性整流单元（Rectified Linear Unit, ReLU），其它类似ReLU的变体包括有斜率的ReLU（Leaky ReLU, LReLU）、参数化的ReLU（Parametric ReLU, PReLU）、随机化的ReLU（Randomized ReLU, RReLU）、指数线性单元（Exponential Linear Unit, ELU）等 。在ReLU出现以前，Sigmoid函数和双曲正切函数（hyperbolic tangent）是常用的激励函数 。如下图。

池化层（Pooling）

池化层不改变三维矩阵的深度，但是可以缩小矩阵的大小。池化操作可以认为是将一张分辨率高的图片转化为分辨率较低的图片。通过池化层，可以进一步缩小最后全连接层中节点的个数，从而到达减少整个神经网络参数的目的。池化层本身没有可以训练的参数。
最大池化是指把卷积后函数区域内元素的最大值作为函数输出的结果，对输入图像提取局部最大响应，选取最显著的特征。平均池化是指把卷积后函数区域内元素的算法平均值作为函数输出结果，对输入图像提取局部响应的均值。如下图。

全连接层

经过多轮卷积层和池化层的处理后，在CNN的最后一般由1到2个全连接层来给出最后的分类结果。经过几轮卷积和池化操作，可以认为图像中的信息已经被抽象成了信息含量更高的特征。我们可以将卷积和池化看成自动图像提取的过程，在特征提取完成后，仍然需要使用全连接层来完成分类任务。
对于多分类问题，最后一层激活函数可以选择 softmax，这样我们可以得到样本属于各个类别的概率分布情况。

二、 LeNet-5详解及代码实现

LeNet是在1998年LeCuu等人提出来的，论文地址：Gradient-Based Learning Applied to Document Recognition
论文详解可以参考博客：CNN入门算法LeNet-5介绍（论文详细解读）

1. LeNet模型详解

LeNet5 这个网络虽然很小，但是它包含了深度学习的基本模块：卷积层，池化层，全连接层。

LeNet-5共有7层，不包含输入，每层都包含可训练参数；每个层有多个Feature Map，每个FeatureMap通过一种卷积滤波器提取输入的一种特征，然后每个FeatureMap有多个神经元。
各层参数详解：

1. INPUT输入层
   输入图片的大小为：32 * 32
   注：输入层不算是网络层次结构之一。
2. C1层 - 卷积层
   输入： 32 * 32
   卷积核大小： 6 * 6
   卷积核种类： 6
   输出featureMap的大小为：28 （32 - 5 + 1）
   神经元数量：28 * 28 * 6
   可训练参数：（5 * 5 + 1) * 6
   连接数：（5 * 5 + 1）* 6 * 28 * 28
3. S2层 - 池化层
   输入：28 * 28
   采样区域：2 * 2
   采样方式：4个输入相加，乘以一个可训练参数，再加上一个可训练偏置。结果通过sigmoid
   采样种类：6
   输出featureMap大小：14 * 14 （28 / 2）
   神经元数量：14 * 14 * 6
   连接数：（2 * 2 + 1）* 6 * 14 * 14
4. C3层 - 卷积层
   输入： 14 * 14
   卷积核大小：5 * 5
   卷积核种类：16
   输出featureMap大小：10 * 10 (14 - 5 + 1)
   可训练参数： 6 * (3 * 5 * 5 + 1) + 6 * (4 * 5 * 5 + 1)+3*(4 * 5 * 5 + 1) + 1 * (6 * 5 * 5 + 1)
   连接数：10 * 10 * （ 15 + 16 ）
5. S4层 - 池化层
   输入： 10 * 10
   采样区域：2*2
   采样方式：4个输入相加，乘以一个可训练参数，再加上一个可训练偏置。结果通过sigmoid
   采样种类：16
   输出featureMap大小：5 * 5 （10/2）
   神经元数量：5 * 5 * 16
   连接数：16 （ 2 * 2 + 1） 5 * 5
6. C5层 - 卷积层
   输入： 5 * 5
   卷积核大小：5 * 5
   卷积核种类：120
   输出featureMap大小：1 * 1 （ 5 - 5 + 1）
   可训练参数/连接：120*（16 * 5 * 5 + 1）
7. F6层 - 全连接层
   输入： 120维向量
   计算方式：计算输入向量和权重向量之间的点积，再加上一个偏置，结果通过sigmoid函数输出。
   可训练参数:84 * ( 120 + 1 )
8. Output层 - 全连接层
   Output层也是全连接层，共有10个节点，分别代表数字0到9，且如果节点i的值为0，则网络识别的结果是数字i。采用的是径向基函数（RBF）的网络连接方式。假设x是上一层的输入，y是RBF的输出，则RBF输出的计算方式是：$$y_i=\sum _j(x_j-w_{ij}{)}^2$$
   上式$w_{ij}$，i从0到9，j取值从0到7 *12-1。RBF输出的值越接近于0，则越接近于i，即越接近于i的ASCII编码图，表示当前网络输入的识别结果是字符i。该层有84x10=840个参数和连接。

2. 代码实现

from keras.models import Sequential
from keras.layers import Input, Dense, Activation, Conv2D, MaxPooling2D, Flatten
from keras.datasets import mnist

# 加载和准备数据集
(x_train, y_train), (x_test, y_test) = mnist.load_data()

# astype修改数据类型
x_train = x_train.reshape(-1, 28, 28, 1)
x_train = x_train.astype('float32')
print(x_train.shape)
y_train = y_train.astype('float32')
x_test = x_test.reshape(-1, 28, 28, 1)
x_test = x_test.astype('float32')
y_test = y_test.astype('float32')
print(y_train)
# 归一化
x_train /= 255
x_test /= 255

from keras.utils import np_utils

y_train_new = np_utils.to_categorical(num_classes=10, y=y_train)
print(y_train_new)
y_test_new = np_utils.to_categorical(num_classes=10, y=y_test)


# 数据预处理
def LeNet_5():
    model = Sequential()
    model.add(Conv2D(filters=6, kernel_size=(5, 5), padding='valid', activation='tanh', input_shape=[28, 28, 1]))
    model.add(MaxPooling2D(pool_size=(2, 2)))
    model.add(Conv2D(filters=16, kernel_size=(5, 5), padding='valid', activation='tanh'))
    model.add(MaxPooling2D(pool_size=(2, 2)))
    model.add(Flatten())
    model.add(Dense(120, activation='tanh'))
    model.add(Dense(84, activation='tanh'))
    model.add(Dense(10, activation='softmax'))
    return model


# 训练模型
def train_model():
    model = LeNet_5()
    model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
    model.fit(x_train, y_train_new, batch_size=64, epochs=20, validation_split=0.2, shuffle=True)
    return model


model = train_model()
# 返回测试集损失函数值和准确率
loss, accuracy = model.evaluate(x_test, y_test_new)
print(loss, accuracy)

三、参考资料

https://www.cnblogs.com/longsongpong/p/11721034.html
https://blog.csdn.net/fly_wt/article/details/95599187