深度强化学习笔记——基本方法分类与一般思路

概要

本文梳理了一下台大李宏毅老师的深度强化学习系列课程内容。该课程主要是对无模型深度强化学习方法的一些大致介绍，将其分为大致三类：基于值函数的、基于梯度的方法、actor-critic的方法。（其他方法还有模仿学习imitation learning与逆强化学习inverse reinforcement learning）

分类方法可以见下图：

本文对三大类方法的基本思路进行阐述，为了写作的方便，文中的图大部分来自课件中的原图。有任何不准确的地方望指正！

1. 基于梯度的方法（Policy-based）

1.1 一般思路

基于梯度的方法可以分为三个步骤：
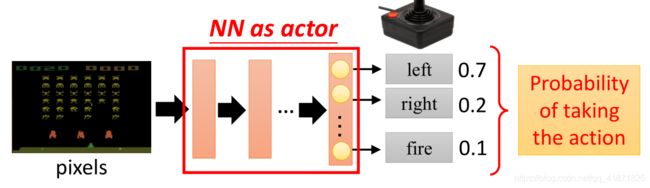
a. 将神经网络作为actor:
在强化学习中，策略就是从状态到动作的一个映射（确定性策略 $a=\pi (s)$）或者是动作的概率分布（随机策略 $\pi (a|s)$），在深度强化学习中，该映射是通过一个神经网络模型来获取的，该网络的输入是状态（比如在游戏中的某一帧或多帧游戏画面，输出是动作的概率分布）

b. 设置损失函数
在深度学习中，神经网络模型的参数更新必须基于某个“标准”，即损失函数的确定，常见的损失函数有交叉熵函数或者均方误差函数等。深度强化学习中的损失函数是多个episodes所获得收益的期望值，并在样本无穷多的假设下，一般用均值来估计该期望值。公式如下：
$${\bar{R}}_{\theta }=\sum _{\tau }R(\tau )P(\tau |\theta )\approx \frac{1}{N}\sum _{n=1}^{N}R({\tau }^n)$$
其中，$\tau =\{s_1,a_1,r_2,s_2,a_2,r_3,\dots ,s_T,a_T,r_{T+1}\}$代表一个episode产生的轨迹（Trajectory）；$T$代表的是到达终止状态的时刻（或者是step）；$R(\tau )={\sum }_{t=1}^T{r}_t$代表每一个episode所得到的所有受益之和（不考虑折扣因素）；而$P(\tau |\theta )$代表着在给定参数为$\theta$的actor的前提下，生成某一个episode所产生的概率大小，这个值一般是很难准确获取的，所以要通过采样的方法对其进行估计。这里的 $N$ 代表的是trajectory的数量或者说是采样的次数，直观来说就是每次智能体与环境交互产生的结果，总共交互 $N$ 次，样本也就是可以表达为$\{{\tau }^1,{\tau }^2,\dots ,{\tau }^N\}$。

c. 根据损失函数更新参数
由于强化学习的基本假设就是最大化智能体的收益，所以基于上一步损失函数就可以用梯度上升（Gradient Ascent）算法进行损失函数的优化，最优的参数可以表示为：
$${\theta }^{\ast }=\underset{\theta }{\mathrm{argmax}}{\bar{R}}_{\theta }$$
这里先不用其估计值，而用其定义式：${\bar{R}}_{\theta }={\sum }_{\tau }R(\tau )P(\tau |\theta )$。

而梯度上升算法的基本形式是：
$${\theta }^{new}\leftarrow {\theta }^{old}+\eta \nabla {\bar{R}}_{\theta }$$
下一步就是如何求具体的$\nabla {\bar{R}}_{\theta }$的值：
$$\begin{gathered} \nabla {\bar{R}}_{\theta }=\sum _{\tau }R(\tau )\nabla P(\tau |\theta )=\sum _{\tau }R(\tau )P(\tau |\theta )\nabla \log P(\tau |\theta ) \\ \approx \frac{1}{N}\sum _{n=1}^{N}R({\tau }^n)\nabla \log P({\tau }^n|\theta ) \end{gathered}$$

接下来是如何计算 $P(\tau |\theta )$ 和$\nabla \log P(\tau |\theta )$的问题：
$$\begin{gathered} P(\tau |\theta )=P(s_1,a_1,r_2,\dots ,s_T,a_T,r_{T+1}|\theta ) \\ =P(s_1)P(a_1|s_1,\theta )P(s_2,r_2|a_1,s_1)\dots \\ =P(s_1)\prod _{t=1}^{T}P(a_t|s_t,\theta )P(s_{t+1},r_{t+2}|s_t,a_t) \end{gathered}$$
这里需要注意的是：$P(s_{t+1},r_{t+2}|s_t,a_t)$是MDP中的动态特性，与智能体的决策（或策略）无关，与之有关的只有$P(a_t|s_t,\theta )$，该概率描述了智能体的策略（也可以将其表示为：${\pi }_{\theta }(a_t|s_t)$）

有了概率的表达式，很好计算其对数的梯度：
$$\log P(\tau |\theta )=P(s_1)+\sum _{t=1}^T\log P(a_t|s_t,\theta )+\log P(s_{t+1},r_{t+2}|s_t,a_t)$$$$\nabla \log P(\tau |\theta )=\sum _{t=1}^T\nabla \log P(a_t|s_t,\theta )$$
带入到 $\nabla {\bar{R}}_{\theta }=\frac{1}{N}{\sum }_{n=1}^{N}R({\tau }^n)\nabla \log P({\tau }^n|\theta )$可以得到：
$$\nabla {\bar{R}}_{\theta }=\frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T^n}R({\tau }^n)\nabla \log P(a_t^n|s_t^n,\theta )$$
从而梯度上升的具体表达式可以写成：
$${\theta }^{new}\leftarrow {\theta }^{old}+\eta \frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T^n}R({\tau }^n)\nabla \log P(a_t^n|s_t^n,\theta )$$
为了避免所得到的收益总和一直是正数，这里可以在公式中加入一个负的baseline（类似bias）
$${\theta }^{new}\leftarrow {\theta }^{old}+\eta \frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T^n}(R({\tau }^n)-b)\nabla \log P(a_t^n|s_t^n,\theta )$$
该表达式与深度学习中用交叉熵损失函数训练神经网络是类似的，只不过在梯度前加上了$R(\tau )$这个权值。交叉熵的表达式可以写成：$f(y,\hat{y})=-{\sum }_{i=1}^N\widehat{y_i}\log y_i$，这里的$\widehat{y_i}$为样本的真实标签，且一般来说标签都是独热表示，例如$[1,0,0,\dots ,0]$求交叉熵的梯度时与之无关，交叉熵的梯度为：
$$\nabla f(y,\hat{y})=-\nabla \log y_i$$

1.2 具体算法

(受篇幅限制，之后敲一遍代码之后再更新吧)

TRPO (Trust Region Policy Optimization)

近端策略优化PPO (Proximal Policy Optimization)
基本步骤：
Policy Gradient
将On-policy改为Off-policy
Add constraint

PPO2

2. 基于值函数方法（Value-based）

2.1 一般思路

基于值函数的方法学习一个critic, 这个critic不会直接决定智能体的决策，而是起到了如下作用：给定一个智能体采取的策略，并评估其好坏。在获得估算出的值函数之后，智能体会根据该值进行策略的更新。这个过程其实就是广义策略迭代的过程（Generalized Policy Iteration），该类方法分为两个步骤，第一个就是如何评估策略，第二个步骤就是对策略进行贪婪更新，从而在很多步之后达到最优解。

策略评估（Policy Evaluation）
在计算评估策略中，既可以使用状态值函数作为评估对象，也可以使用动作值函数进行评估。在强化学习中，如果环境的模型，即MDP已知，则可以通过动态规划来求解（其评估过程就是用Bellman Equation或者是Bellman Optimality Equation进行状态值或动作值的迭代更新）；如果是无模型的情况，就可以通过Monte-Carlo和Temporal Difference的方法进行估计。其中MC方法是获取许多episodes，在每个episode结束之后更新状态或动作值。TD的估算方法如下：

策略改进（Policy Improvement）
在策略评估结束之后，智能体要根据所获取的评估值对其策略进行改进。一般采用的方法就是贪心地选择能够使动作值最大的某个动作：
$${\pi }^{\prime }(s)=\underset{a}{\mathrm{argmax}}{Q}^{\pi }(s,a)$$
这时所得到的
$$V^{{\pi }^{\prime }}(s)=\underset{a}{\max }{Q}^{\pi }(s,a)\ge V_{\pi }(s)$$
如此更新下去，$V^{{\pi }^{\prime }}(s)$满足贝尔曼最优方程，即所采用的策略${\pi }^{\prime }$一定是最优的。

该方法是基于策略改进定理：如果$V^{\pi }(s)\le Q^{\pi }(s,{\pi }^{\prime }(s))$，则$V^{{\pi }^{\prime }}(s)\ge V^{\pi }(s)$ (这里假设是确定性策略)

证明：
$$\begin{gathered} V^{\pi }(s)\le Q^{\pi }(s,{\pi }^{\prime }(s))=\mathbb{E}[R_{t+1}+\gamma V^{\pi }(S_{t+1})|S_t=s,A_t={\pi }^{\prime }(s)]={\mathbb{E}}_{{\pi }^{\prime }}[R_{t+1}+\gamma V^{\pi }(S_{t+1})|S_t=s] \\ \le {\mathbb{E}}_{{\pi }^{\prime }}[R_{t+1}+\gamma Q^{\pi }(S_{t+1})|S_t=s] \\ ={\mathbb{E}}_{{\pi }^{\prime }}[R_{t+1}+\gamma R_{t+2}+{\gamma }^2{V}^{\pi }(S_{t+2})|S_t=s] \\ \dots \\ \le {\mathbb{E}}_{{\pi }^{\prime }}[R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+\dots |S_t=s] \\ =V^{\pi }(s) \end{gathered}$$

2.2 具体算法

Q-learning及其变体

Q-learning的基本组成元素：
目标网络（Target Network）
$ϵ$-greedy exploration
经验重放缓冲器（Experience Replay Buffer）

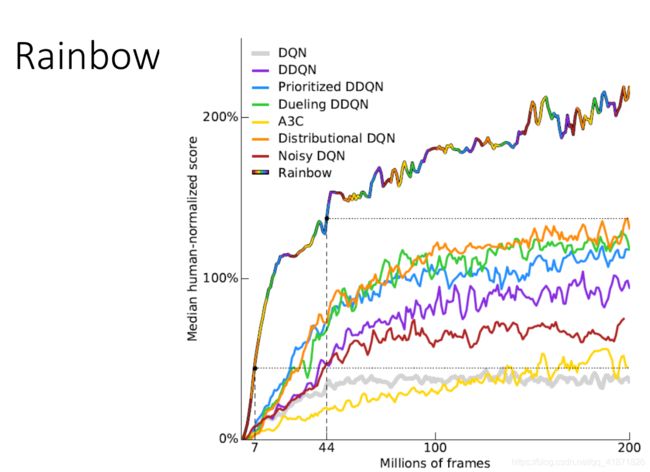
Q-learning使用的七种技巧被总结成了“rainbow”图像。

3. Actor-Critic

3.1 一般思路

对policy gradient做了简单的修改，引入了Advantage Function,也就是将其中的总收益$R({\tau }^n)$改为由critic评估的动作值与状态值的差值：
$$R({\tau }^n)-b\to Q^{{\pi }_{\theta }}(s_t,a_t)-V^{{\pi }_{\theta }}(s_t)$$
如果按以上的表达式进行修改，那么actor-critic算法中可能需要涉及两个网络的训练，但其实可以通过动作值与状态值的关系：$Q^{\pi }(s,a)={\sum }_{s^{\prime },r}p(s^{\prime },r|s,a)(r+V^{\pi }(s^{\prime }))$粗略地化简上式中动作值与状态值的差值，以实现对一个网络进行训练，即
$$Q^{{\pi }_{\theta }}(s_t,a_t)-V^{{\pi }_{\theta }}(s_t)\to r_t^n+V^{{\pi }_{\theta }}(s_{t+1})-V^{{\pi }_{\theta }}(s_t)$$
那么梯度上升的部分就变成了：
$${\theta }^{new}\leftarrow {\theta }^{old}+\eta \frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T^n}(r_t^n+V^{{\pi }_{\theta }}(s_{t+1})-V^{{\pi }_{\theta }}(s_t))\nabla \log P(a_t^n|s_t^n,\theta )$$
通过以上的公式也就将基于策略的与基于值函数的方法融合在了一起，也就是actor-critic的一般思路。

3.2 具体算法

A2C （Advantage Actor-Critic）

A3C（Asynchronous Advantage Actor-Critic）

Pathwise Derivative Policy Gradient
(类似于交替训练两个网络的GAN网络)

4. 模仿学习（Imitation Learning）

IL又称为learning by demonstration或者apprenticeship learning，本质上其实是监督学习的一种。大致的过程就是一个专家（可以是人也可以是好的训练数据）演示如何完成某个任务，之后机器根据专家的“演示”进行学习。该方法适用于收益函数很难定义的情况。IL有两种方法：行为克隆（Behavior Cloning）和逆强化学习（Inverse Reinforcement Learning）。

行为克隆（Behavior Cloning）

该方法属于监督学习，因为有已知的训练数据。

可能遇到的问题：
在机器的学习能力有限的情况下，在学习过程中机器可能会选择错误的行为。并且在该算法过程中训练数据和测试数据不一定满足独立同分布的假设。

逆强化学习（Inverse Reinforcement Learning）

思路：首先获取专家的演示数据或轨迹，经过逆强化学习过程中与环境的交互之后，推导出收益函数，并且用该收益函数，再基于强化学习的方法找到最优的策略。

具体的逆强化学习模型算法一般是由两个网络组成，一个是专家网络，一个是actor网络，类似于GAN, actor和expert两个网络产生的收益函数不断做对比，最后生成一个近乎一样好的收益函数。