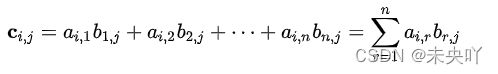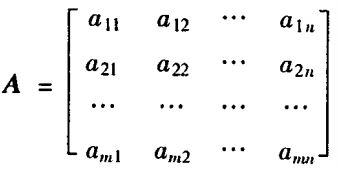《C语言》矩阵问题
一.矩阵乘法
1.定理:
两个矩阵的乘法仅当第一个矩阵A的列数和另一个矩阵B的行数相等时才能定义。如A是m×n矩阵和B是n×p矩阵,它们的乘积C是一个m×p矩阵。
2.思路
1. i,j分别代表行和列,所以应该定义一个二维矩阵,其行和列都为2.
2.分析一下上面这个公式设a*b=C,C为矩阵乘法后的结果。
(1)C的第一行
C的第一行第一列等于a的第一行的每一个值乘b的第一列的每一个值
C的第一行第二列等于a的第一行的每一个值乘b的第二列的每一个值
(2)C的第二行
C的第二行第一列等于a的第二行的每一个值乘b的第一列的每一个值
C的第二行第二列等于a的第二行的每一个值乘b的第二列的每一个值
3.代码实现
#include
main()
{
int n = 0;
int ret1[2][3] = { {1,0,2}, {-1,3,1} };
int ret2[3][2] = { {3,1},{2,1},{1,0} };
int ret3[2][2];
for (int i = 0; i < 2; i++)
{
for (int j = 0; j < 2; j++)
{
ret3[i][j] = 0; //每次初始化为0
for (int k = 0; k < 3; k++)
{
ret3[i][j] += ret1[i][k] * ret2[k][j];
}
}
}
for (int i = 0; i < 2; i++) //输出
{
for (int j = 0; j < 2; j++)
{
printf("%d\t", ret3[i][j]);
}
printf("\n");
}
} 二.转置矩阵
1.定义:把m*n矩阵
行和列互换之后得到的矩阵
2.题目
给你一个二维整数数组
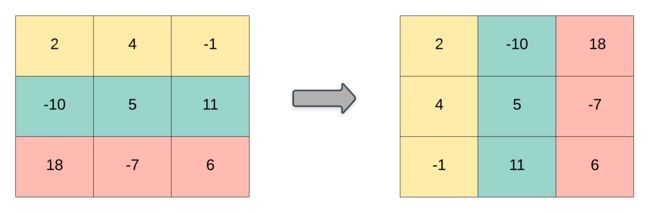
matrix, 返回matrix的 转置矩阵 。矩阵的 转置 是指将矩阵的主对角线翻转,交换矩阵的行索引与列索引。
<1>思路:
直接令行索引和列索引交换即可
<2>代码
#include
main()
{
int ret[3][3] = { {2,4,-1},{-10,5,11},{18,-7,6} };//定义一个二维矩阵
int newret[3][3]; //新定义一个矩阵
for (int i = 0; i < 3; i++) //分别遍历行和列
{
for (int j = 0; j < 3; j++)
{
newret[i][j] = ret[j][i]; //列索引行索引交换
printf("%d\t", newret[i][j]);
}
printf("\n");
}
} <3>结果
三.矩阵旋转
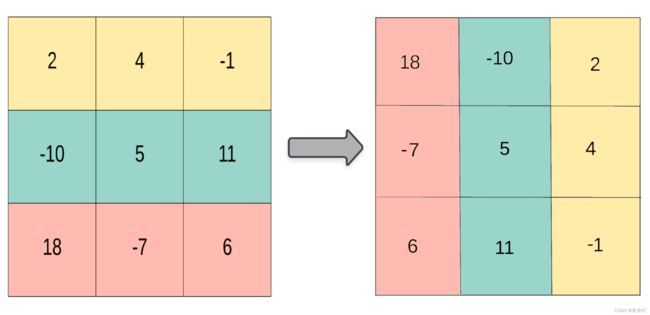
顺时针旋转90°
1.思路
4的坐标的变化:(0,1)--->(1,1)
其他数都是一样的规律就不一一列举出来
对于矩阵中第 i 行的第 j个元素,在旋转后,它出现在倒数第 i 列的第 j 个位置。
翻译成代码
对于矩阵的元素matrix[i][j] 在旋转后变成matrix2[j][n-i-1];在下列代码中n为3,
2.代码
<1>根据上述规则,进行矩阵的旋转把matrix的元素放入到matrix2。
<2>输出旋转后的矩阵
{
int matrix[3][3] = { 2,4,-1,-10,5,11,18,-7,6 };
int matrix2[3][3];
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
matrix2[j][3-i-1] = matrix[i][j]; //根据规则旋转矩阵
}
}
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
printf("%d\t", matrix2[i][j]); //输出旋转后的矩阵
}
printf("\n");
}
}
逆时针旋转90°(等同于逆时针旋转270°)
1.思路
4:(0,1)--->(1,0)
其他数都是一样的规律就不一一列举出来
对于矩阵中第 i 行的第 j个元素,在旋转后,它出现在倒数第 i 列的第 j 个位置。
翻译成代码
对于矩阵的元素matrix[j][n-i-1] 在旋转后变成matrix2[i][j] ;在下列代码中n为3,
2.代码
<1>根据上述规则,进行矩阵的旋转把matrix的元素放入到matrix2。
<2>输出旋转后的矩阵
{
int matrix[3][3] = { 2,4,-1,-10,5,11,18,-7,6 };
int matrix2[3][3];
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
matrix2[i][j] = matrix[j][3-1-i]; //跟顺时针旋转的区别
}
}
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
printf("%d\t", matrix2[i][j]);
}
printf("\n");
}
}
顺时针旋转180°(等同于逆时针旋转180°)
1.思路
4:(0,1)--->(2,1)
其他数都是一样的规律就不一一列举出来
对于矩阵中第 i 行的第 j个元素,在旋转后,它出现在倒数第 i 列的第 j 个位置。
翻译成代码
对于矩阵的元素matrix[i][j] 在旋转后变成matrix2[n-j-1][n-i-1];在下列代码中n为3,
2.代码
<1>根据上述规则,进行矩阵的旋转把matrix的元素放入到matrix2。
<2>输出旋转后的矩阵
main()
{
int matrix[3][3] = { 2,4,-1,-10,5,11,18,-7,6 };
int matrix2[3][3];
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
matrix2[3 - i - 1][3 - j - 1] = matrix[i][j];
}
}
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
printf("%d\t", matrix2[i][j]);
}
printf("\n");
}
}