数位DP 详解及其案例实战Ⅱ
零. 案例引入
1.案例引入 leetcode233. 数字 1 的个数
2.暴力解
3.引出数位DP
一. 数位DP简单介绍
1.数位DP的本质
2.数位DP适合处的问题
3.数位DP在实际使用面临什么难点
二. 数位DP典型模板和技巧
1.模板
2.模板解读
3.相关技巧总结
三. 数位DP案例
1.leetcode233 数字 1 的个数
2. leetcode 2376 统计特殊整数
3. leetcode1012 至少有 1 位重复的数字
以上部分不再赘述,可参考前篇:
数位DP 详解及其案例实战 [模板+技巧+案例]
4. leetcode 面试题 17.06. 2出现的次数
编写一个方法,计算从 0 到 n (含 n) 中数字 2 出现的次数。
输入: 25
输出: 9
解释: (2, 12, 20, 21, 22, 23, 24, 25)(注意 22 应该算作两次)代码
class Solution {
char[] ch;
int[][] memo;
public int numberOf2sInRange(int n) {
ch = Integer.toString(n).toCharArray();
memo = new int[ch.length][ch.length];
for(int[] arr : memo){
Arrays.fill(arr , -1);
}
return dfs(0,0,true);
}
public int dfs(int pos, int ctTwo, Boolean isLimit){
if(pos == ch.length) return ctTwo;
if(!isLimit && memo[pos][ctTwo] != -1) return memo[pos][ctTwo];
int up = isLimit ? ch[pos] - '0' : 9;
int ans = 0;
for(int d = 0; d <= up; d++){
ans += dfs(pos+1,ctTwo + (d == 2 ? 1 : 0), isLimit && d == up);
}
if(!isLimit) memo[pos][ctTwo] = ans;
return ans;
}
}行注释
本题小结:(1)此题和 leetcode233 数字 1 的个数 属于同一类题目,不再赘述
5. leetcode 902. 最大为 N 的数字组合
给定一个按 非递减顺序 排列的数字数组 digits 。你可以用任意次数 digits[i] 来写的数字。例如,如果 digits = ['1','3','5'],我们可以写数字,如 '13', '551', 和 '1351315'。
返回 可以生成的小于或等于给定整数 n 的正整数的个数 。
输入:digits = ["1","3","5","7"], n = 100
输出:20
解释:
可写出的 20 个数字是:
1, 3, 5, 7, 11, 13, 15, 17, 31, 33, 35, 37, 51, 53, 55, 57, 71, 73, 75, 77.输入:digits = ["1","4","9"], n = 1000000000
输出:29523
解释:
我们可以写 3 个一位数字,9 个两位数字,27 个三位数字,
81 个四位数字,243 个五位数字,729 个六位数字,
2187 个七位数字,6561 个八位数字和 19683 个九位数字。
总共,可以使用D中的数字写出 29523 个整数。
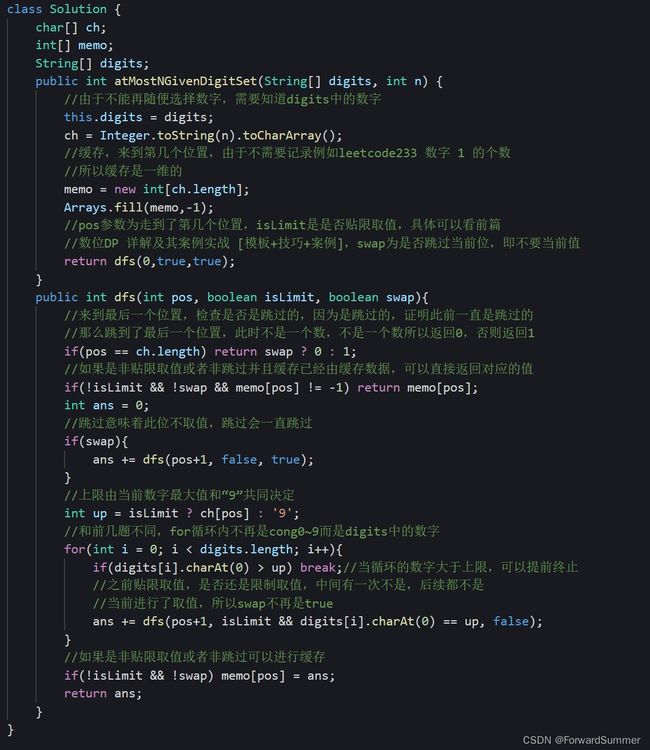
代码
class Solution {
char[] ch;
int[] memo;
String[] digits;
public int atMostNGivenDigitSet(String[] digits, int n) {
this.digits = digits;
ch = Integer.toString(n).toCharArray();
memo = new int[ch.length];
Arrays.fill(memo,-1);
return dfs(0,true,true);
}
public int dfs(int pos, boolean isLimit, boolean swap){
if(pos == ch.length) return swap ? 0 : 1;
if(!isLimit && !swap && memo[pos] != -1) return memo[pos];
int ans = 0;
if(swap){
ans += dfs(pos+1, false, true);
}
int up = isLimit ? ch[pos] : '9';
for(int i = 0; i < digits.length; i++){
if(digits[i].charAt(0) > up) break;
ans += dfs(pos+1, isLimit && digits[i].charAt(0) == up, false);
}
if(!isLimit && !swap) memo[pos] = ans;
return ans;
}
}行注释
本体小结:(1)此题和前面的题目最大不同就是数字的选择是固定的,不是从1~9选择
(2)由于是符合实际的数字,那么swap标志位是需要的
(3)isLimit位和swap共同决定了缓存的存储问题
(4)此题的缓存只有一维,不需要记录前面有没有用的特殊的数字
6. leetcode600 不含连续1的非负整数
给定一个正整数 n ,请你统计在 [0, n] 范围的非负整数中,有多少个整数的二进制表示中不存在 连续的 1 。
输入: n = 5
输出: 5
解释:
下面列出范围在 [0, 5] 的非负整数与其对应的二进制表示:
0 : 0
1 : 1
2 : 10
3 : 11
4 : 100
5 : 101
其中,只有整数 3 违反规则(有两个连续的 1 ),其他 5 个满足规则。
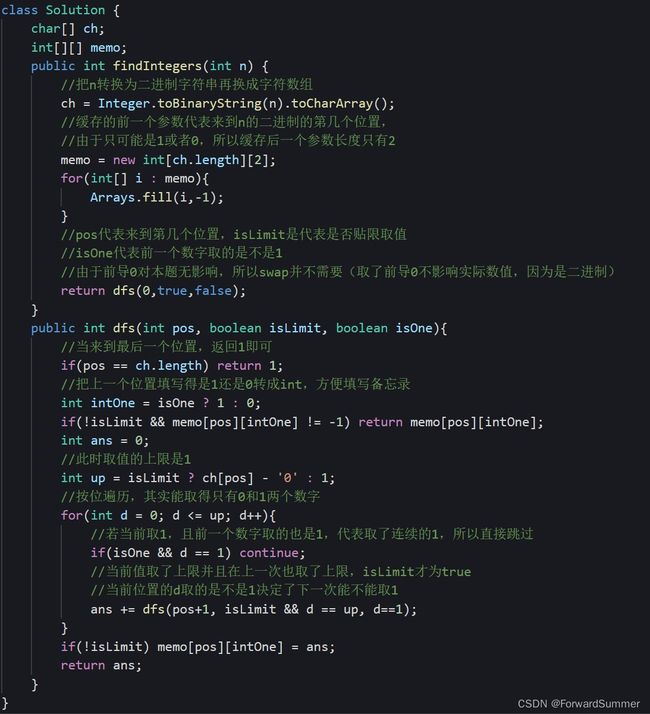
代码
class Solution {
char[] ch;
int[][] memo;
public int findIntegers(int n) {
ch = Integer.toBinaryString(n).toCharArray();
memo = new int[ch.length][2];
for(int[] i : memo){
Arrays.fill(i,-1);
}
return dfs(0,true,false);
}
public int dfs(int pos, boolean isLimit, boolean isOne){
if(pos == ch.length) return 1;
int intOne = isOne ? 1 : 0;
if(!isLimit && memo[pos][intOne] != -1) return memo[pos][intOne];
int ans = 0;
int up = isLimit ? ch[pos] - '0' : 1;
for(int d = 0; d <= up; d++){
if(isOne && d == 1) continue;
ans += dfs(pos+1, isLimit && d == up, d==1);
}
if(!isLimit) memo[pos][intOne] = ans;
return ans;
}
}行注释
二进制遍历注意点
(1)数字取值范围不再是0~9,而是0~1,相应得上限也从9变成1
(2)由于二进制遍历只有两种可能,那么相应的遍历也可以根据题目简化,在本题中for循环可以写成{Ref【1】}:
var res = f(i + 1, false, isLimit && up == 0); // 填 0
if (!pre1 && up == 1) res += f(i + 1, true, isLimit); // 填 1
本体小结:(1)重点需要保存上一个取值取得是不是1,若上一次取1且当位置又取了1,那么本轮得结果不符合题目要求,直接跳过
(2)备忘录里是来到第pos个位置,取值是1还是0得两种可能性的备忘录
(3)由于前导0对本题无影响,所以swap并不需要(取了前导0不影响实际数值,因为是二进制)
参考来源 Ref.
【1】leetcode 灵茶山艾府 数位 DP 通用模板,附题单(Python/Java/C++/Go)