10000字，我用 Python 分析泰坦尼克数据

Titanic数据是一份经典数据挖掘的数据集，本文介绍的是kaggle排名第一的案例分享。

原notebook地址：https://www.kaggle.com/startupsci/titanic-data-science-solutions

排名

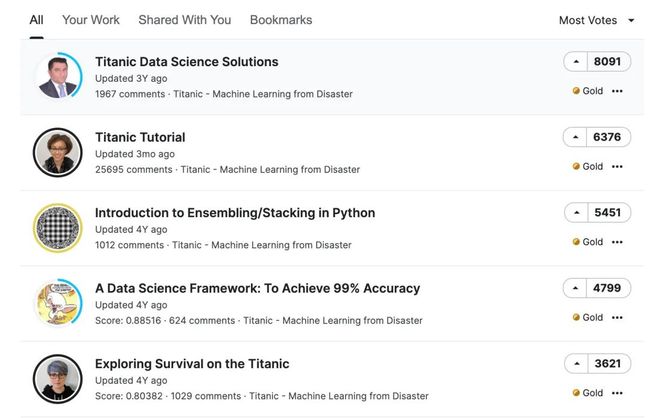
看下这个案例的排名情况：

第一名和第二名的差距也不是很多，而且第二名的评论远超第一名；有空再一起学习下第二名的思路。

通过自己的整体学习第一名的源码，前期对字段的处理很细致，全面；建模的过程稍微比较浅。

数据集如何领取？

技术要学会分享、交流，不建议闭门造车。一个人走的很快、一堆人可以走的更远。

文章中的源码、资料、数据、技术交流提升， 均可加知识星球交流群获取，群友已超过2000人，添加时切记的备注方式为：来源+兴趣方向，方便找到志同道合的朋友。

方式①、添加微信号：pythoner666，备注：来自 CSDN + 泰坦尼克号
方式②、微信搜索公众号：Python学习与数据挖掘，后台回复：加群

数据探索

导入库

导入整个过程中需要的三类库：

• 数据处理

• 可视化库

• 建模库

# 数据处理
import pandas as pd
import numpy as np
import random as rnd

# 可视化
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline

# 模型
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC, LinearSVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import Perceptron
from sklearn.linear_model import SGDClassifier
from sklearn.tree import DecisionTreeClassifier

导入数据

导入数据后查看数据的大小

字段信息

查看全部的字段：

train.columns

Index(['PassengerId', 'Survived', 'Pclass', 'Name', 'Sex', 'Age', 'SibSp',
       'Parch', 'Ticket', 'Fare', 'Cabin', 'Embarked'],
      dtype='object')

下面是字段的具体含义:

• PassengerId：用户id

• survival：是否生还，0-否，1-是

• pclass：舱位，1-头等舱，2-二等，3-三等

• name：姓名

• sex：性别

• Age：年龄

• sibsp：在船上的兄弟/配偶数

• parch：在船上父母/孩子数

• ticket：票号

• fare：票价

• cabin：Cabin number；客舱号

• embarked：登船地点

字段分类

本案例中的数据主要是有两种类型：

• 分类型Categorical: Survived, Sex, and Embarked. Ordinal: Pclass

• 连续型Continous: Age, Fare. Discrete: SibSp, Parch

缺失值

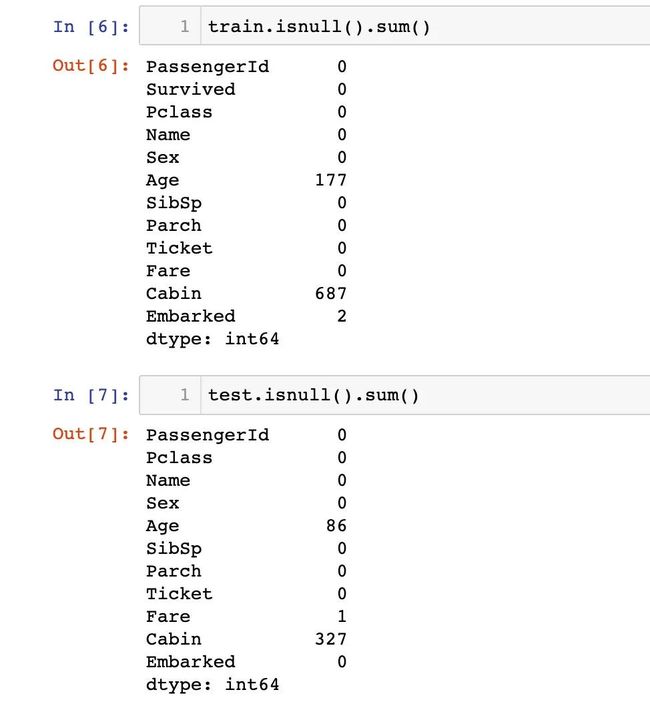
查看训练集和测试集的缺失值情况：

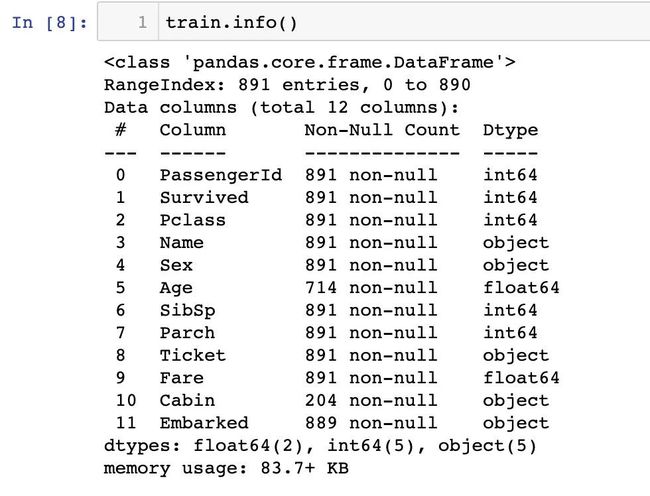
同时也可以通过info函数来查数据的基本信息：

数据假设

作者基于数据的基本信息和常识，给出了自己的一些假设和后面的数据处理和分析方向：

删除字段

• 本项目主要是考察其他字段和Survival字段的关系

• 重点关注字段：Age、Embarked

• 删除字段：对数据分析没有作用，直接删除的字段：Ticket（票号）、Cabin（客舱号）、PassengerId（乘客号）、Name（姓名）

修改、增加字段

• 增加Family：根据Parch（船上的兄弟姐妹个数） 和 SibSp（船上的父母小孩个数）

• 从Name字段中提取Title作为新特征

• 将年龄Age字段转成有序的分类特征

• 创建一个基于票价Fare 范围的特征

猜想

• 女人（Sex=female）更容易生还

• 小孩（Age>？）更容易生还

• 船舱等级高的乘客更容易生还（Pclass=1）

统计分析

主要是对分类的变量Sex、有序变量Pclss、离散型SibSp、Parch进行分析来验证我们的猜想

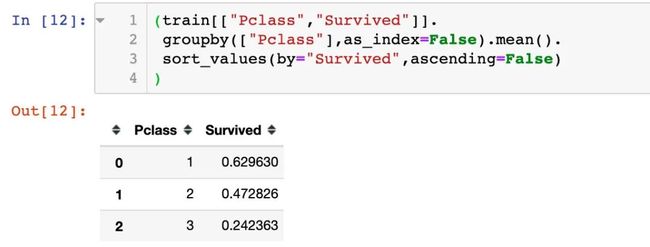
1、船舱等级（1-头等，2-二等，3-三等）

结论：头等舱的人更容易生还

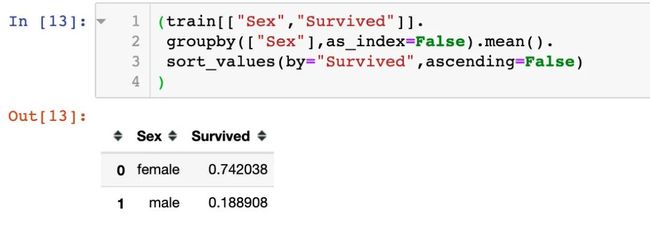
2、性别

结论：女人更容易生还

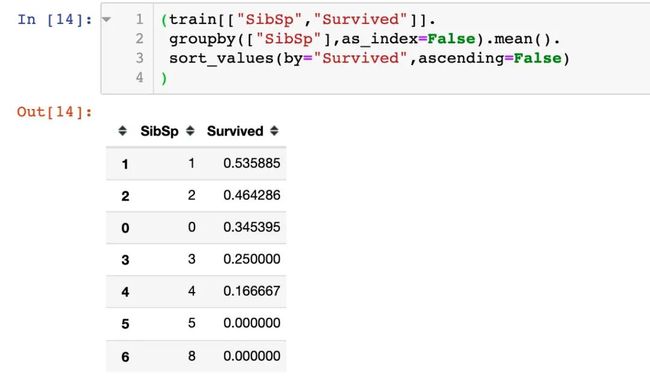
3、兄弟姐妹/配偶数

结论：兄弟姐妹或者配偶数量相对少的乘客更容易生还

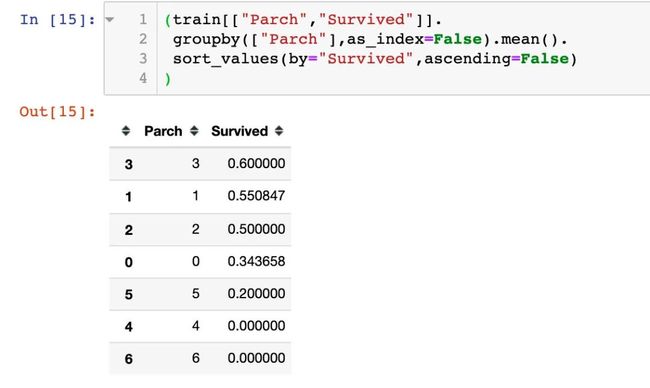
4、父母/孩子数

结论：父母子女在3个的时候，更容易生还

可视化分析

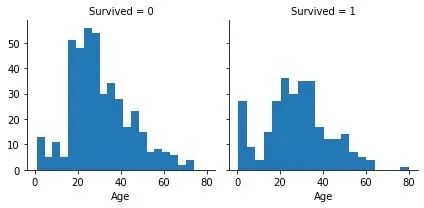
年龄与生还

g = sns.FacetGrid(train, col="Survived")
g.map(plt.hist, 'Age', bins=20)

plt.show()

1. 对于未生还的人员，大多数集中在15-25岁（左图）

2. 生还人员年龄最大为80；同时4岁以下的小孩生还率很高（右图）

3. 乘客的年龄大多数集中在15-35岁（两图）

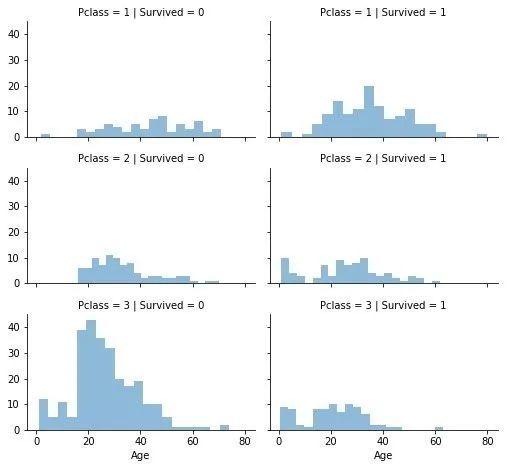
舱位与生还

grid = sns.FacetGrid(
    train,
    col="Survived",
    row="Pclass",
    size=2.2,
    aspect=1.6
    )

grid.map(plt.hist,"Age",alpha=0.5,bins=20)
grid.add_legend()
plt.show()

• 舱位等级3的乘客最多；但是很多没有生还

• 舱位等级1的乘客生还最多

登船地点、性别与生还的关系

grid = sns.FacetGrid(train,
                     row="Embarked",
                     size=2.2,
                     aspect=1.6)
grid.map(sns.pointplot,
         "Pclass",
         "Survived",
         "Sex",
         palette="deep")

grid.add_legend()

plt.show()

1. 女性比男性的生还情况要好

2. 除了在Embarked=C，男性的生还率要高些。

3. 当舱位等级都在Pclass=3，男性的在Embarked=C的生还率好于Q

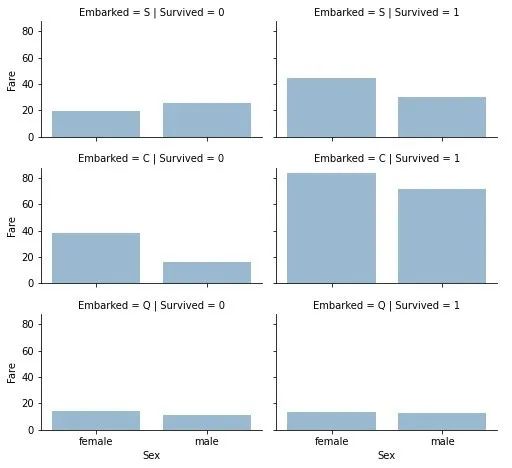
票价、舱位与生还

grid = sns.FacetGrid(train, 
                     row='Embarked', 
                     col='Survived', 
                     size=2.2, aspect=1.6)

grid.map(sns.barplot, 
         'Sex', 
         'Fare', 
         alpha=.5, ci=None)

grid.add_legend()

plt.show()

• 票价越高，生还效果越好；右侧上2图

• 生还率和登船的位置相关；明显在Embarked=C的情况是最好的

上面都是基于简单的统计和可视化方面的分析，下面的过程是基于各种机器学习建模的方法来进行分析，前期做了很多的预处理好特征工程的工作。

删除无效字段

票价ticket和客舱号Cabin对我们分析几乎是没有用的，可以考虑直接删除：

生成新特征

主要是根据现有的特征属性中找到一定的关系，来生成新的特征，或者进行一定的特征属性转化。

字段Name处理

根据名称Name生成找到称谓，比如Lady、Dr、Miss等信息，来查看这个称谓和生还信息之间是否存在关系

# 通过正则提取
for dataset in combine:
    dataset["Title"] = dataset.Name.str.extract('([A-Za-z]+)\.', expand=False)
    
  # 统计Title下的男女数量
train.groupby(["Sex","Title"]).size().reset_index()

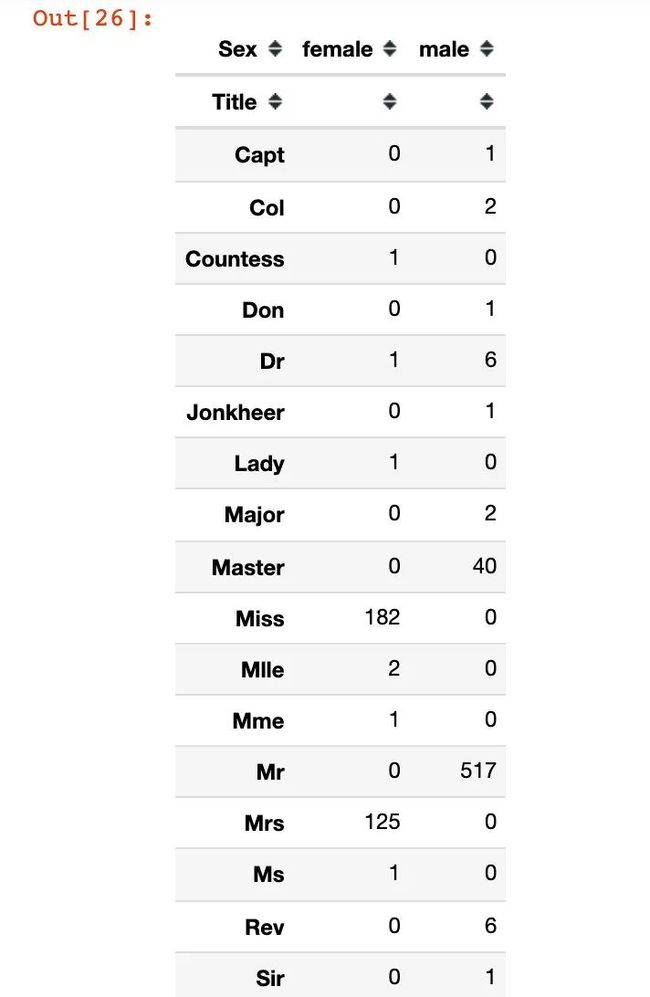
使用交叉表的形式统计：

# 交叉表形式
pd.crosstab(train['Title'], train['Sex'])

将提取出来的称谓进行整理，归类为常见的称谓和Rare信息：

for dataset in combine:
    dataset["Title"] = dataset["Title"].replace(['Lady', 'Countess','Capt', 'Col',\
  'Don', 'Dr', 'Major', 'Rev', 'Sir', 'Jonkheer', 'Dona'], 'Rare')
    
    dataset['Title'] = dataset['Title'].replace('Mlle', 'Miss')
    dataset['Title'] = dataset['Title'].replace('Ms', 'Miss')
    dataset['Title'] = dataset['Title'].replace('Mme', 'Mrs')
    
    
# 根据称谓Title求生还的均值
train[["Title","Survived"]].groupby("Title",as_index=False).mean()

称谓本身是文本型对后期建模无用，我们直接转成数值型：

title_mapping = {
  "Mr":1,
  "Miss":2,
  "Mrs":3,
  "Master":4,
  "Rare":5
}

for dataset in combine:
    # 存在数据的进行匹配
    dataset['Title'] = dataset['Title'].map(title_mapping)
    # 不存在则补0
    dataset['Title'] = dataset['Title'].fillna(0)
    
train.head()

同时还需要删除部分字段：

train = train.drop(['Name', 'PassengerId'], axis=1)
test = test.drop(['Name'], axis=1)

combine = [train, test]
train.shape, test.shape

# ((891, 9), (418, 9))

字段Sex

将性别的Male和Female转成0-Male，1-Female

 for dataset in combine:
    dataset['Sex'] = dataset['Sex'].map( {'female': 1, 'male': 0} ).astype(int)

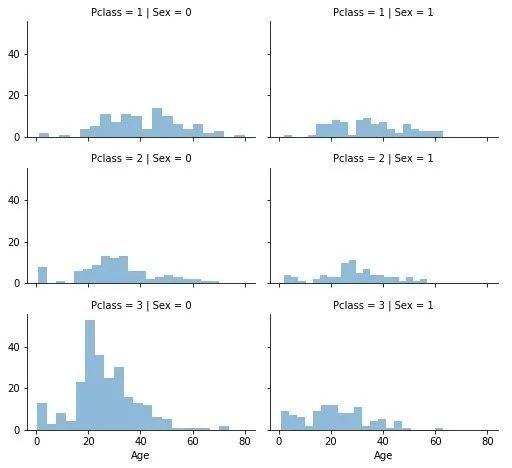
性别、年龄、生还之间的关系：

grid = sns.FacetGrid(
    train,
    row='Pclass',
    col='Sex',
    size=2.2, 
    aspect=1.6)

grid.map(plt.hist, 
         'Age', 
         alpha=.5, 
         bins=20)

grid.add_legend()

plt.show()

字段Age

1、首先就是字段的缺失值处理。

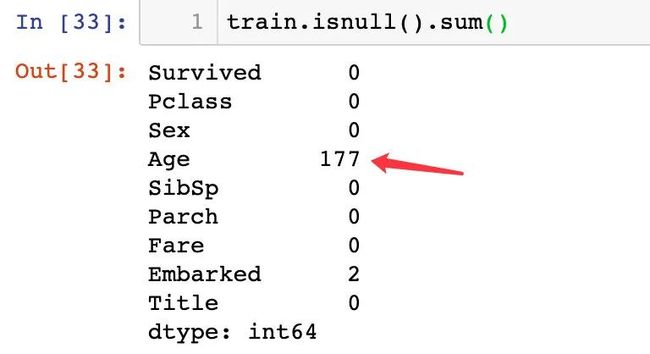
我们观察到年龄字段是存在缺失值的，我们通过Sex（0、1）和Pclass（1、2、3）的6种组合关系来进行填充。缺失值情况：

填充的具体过程：

guess_ages = np.zeros((2,3))

 for dataset in combine:
    for i in range(0,2):
        for j in range(0,3):
            # 找到某种条件下Age字段的缺失值并删除
            guess_df = dataset[(dataset["Sex"] == i) & (dataset["Pclass"] == j+1)]["Age"].dropna()
            age_guess = guess_df.median()  # 中位数
            guess_ages[i,j] = int(age_guess / 0.5 + 0.5) * 0.5
    for i in range(0,2):
        for j in range(0,3):
            dataset.loc[(dataset.Age.isnull()) & (dataset.Sex == i) & (dataset.Pclass == j+1),"Age"] = guess_ages[i,j]
    dataset["Age"] = dataset["Age"].astype(int)
    
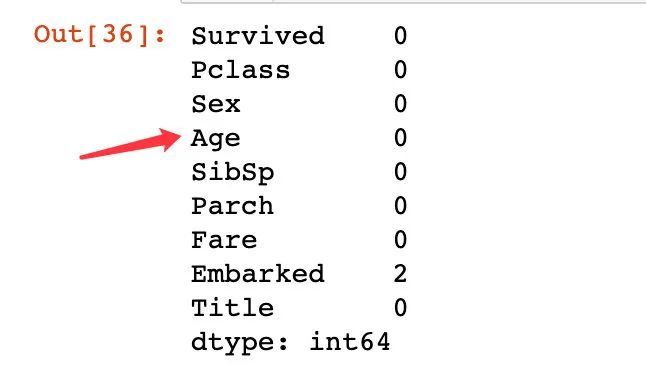
# 填充后不存在缺失值
train.isnull().sum()

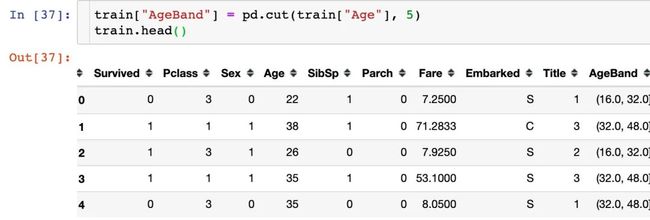
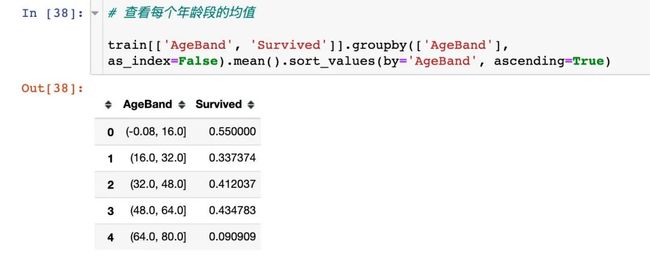
2、年龄分段分箱

3、转成数值分类

• 年龄小于16用0替代

• 16到32用1替代等…

for dataset in combine:
    dataset.loc[dataset["Age"] <= 16, "Age"] = 0
    dataset.loc[(dataset["Age"] > 16) & (dataset["Age"] <= 32), "Age"] = 1
    dataset.loc[(dataset["Age"] > 32) & (dataset["Age"] <= 48), "Age"] = 2
    dataset.loc[(dataset["Age"] > 48) & (dataset["Age"] <= 64), "Age"] = 3
    dataset.loc[(dataset["Age"] > 64), "Age"] = 4
    
# 删除年龄段AgeBand字段
train = train.drop(["AgeBand"], axis=1)
combine = [train, test]

字段处理

根据现有的字段来生成新字段：

生成新字段1

首先根据Parch和SibSp两个字段生成一个FamilySize字段

for dataset in combine:
    dataset["FamilySize"] = dataset["SibSp"] + dataset["Parch"] + 1

    
# 每个FamilySize的生还均值
train[['FamilySize', 'Survived']].groupby(['FamilySize'], as_index=False).mean().sort_values(by='Survived', ascending=False)

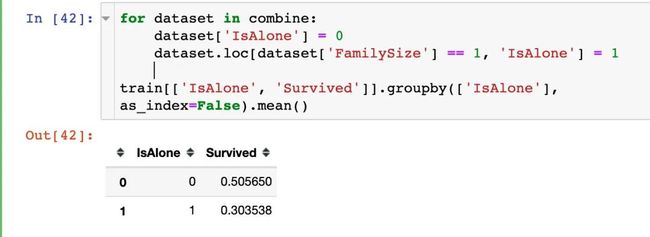
根据字段FamilySize来判断是否Islone：如果家庭成员FamilySize是一个人，那肯定是Islone的，用1表示，否则用0表示

最后将 Parch, SibSp, and FamilySize删除，仅保留是否一个人Islone：

# 将 Parch, SibSp, and FamilySize删除，仅保留是否一个人Islone

train = train.drop(['Parch', 'SibSp', 'FamilySize'],axis=1)
test = test.drop(['Parch', 'SibSp', 'FamilySize'],axis=1)
combine = [train, test]

train.head()

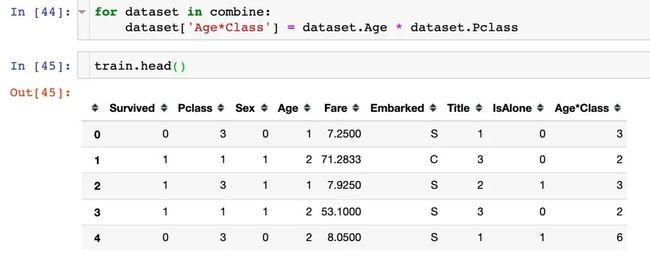
生成新字段2

新字段2是Age和Pclass的乘积：

Embarked字段的分类

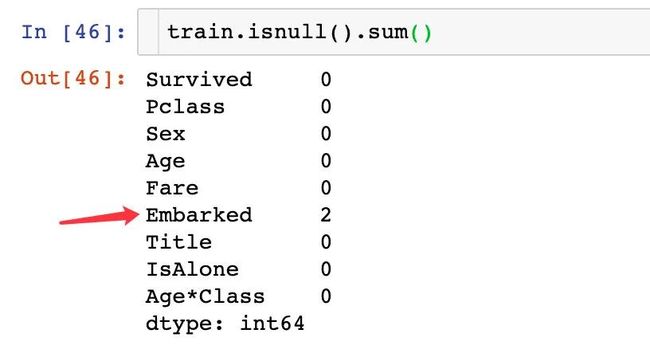
Embarked字段取值有SQC。首先我们填充里面的缺失值

查看这个字段是存在缺失值的：

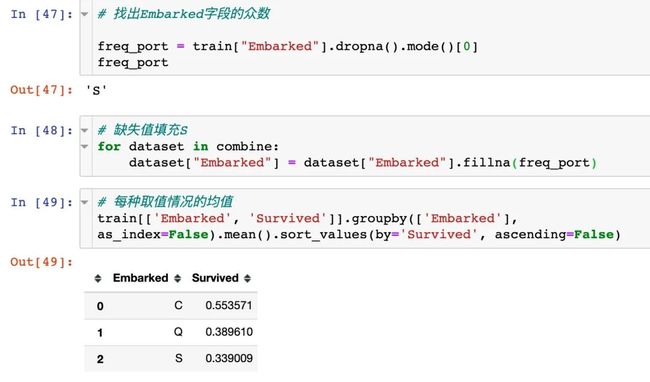
处理：找出众数、填充缺失值、查看每个取值的均值

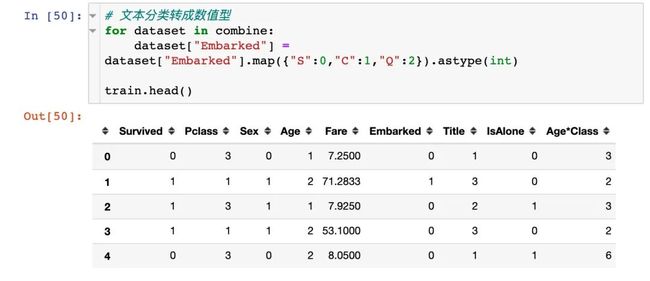
将文本类型转成数值型：

Fare字段处理

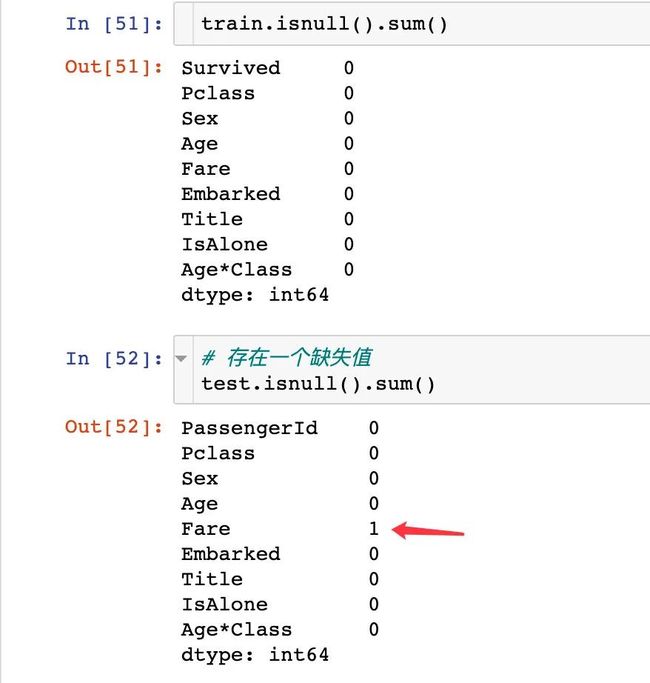
训练集这个字段是没有缺失值，测试集中存在一个：

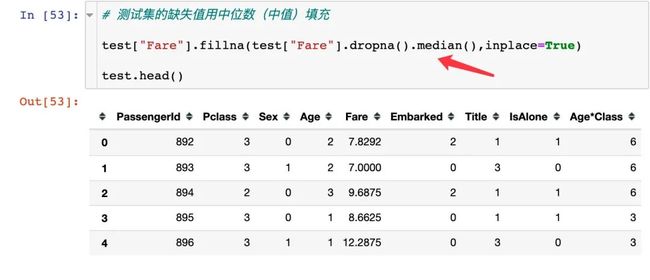
使用中值进行填充：

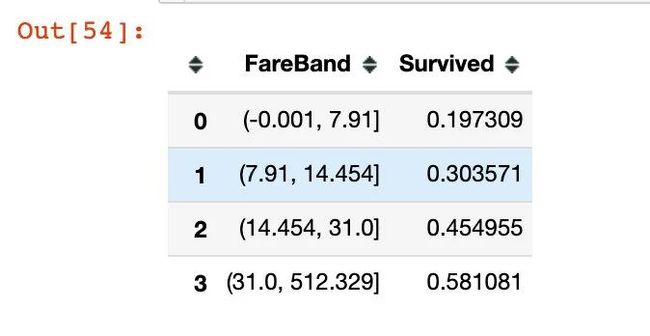
实行分箱操作：

# 只对FareBand字段分箱
train['FareBand'] = pd.qcut(train['Fare'], 4)  # 分成4组

# 生还的均值
train[['FareBand', 'Survived']].groupby(['FareBand'], as_index=False).mean().sort_values(by='FareBand', ascending=True)

将每个段转成数值型的数据：

# 4个分段
for dataset in combine:
    dataset.loc[ dataset['Fare'] <= 7.91, 'Fare'] = 0
    dataset.loc[(dataset['Fare'] > 7.91) & (dataset['Fare'] <= 14.454), 'Fare'] = 1
    dataset.loc[(dataset['Fare'] > 14.454) & (dataset['Fare'] <= 31), 'Fare']   = 2
    dataset.loc[ dataset['Fare'] > 31, 'Fare'] = 3
    dataset['Fare'] = dataset['Fare'].astype(int)

# 
train = train.drop(['FareBand'], axis=1)
combine = [train, test]
    
test.head()

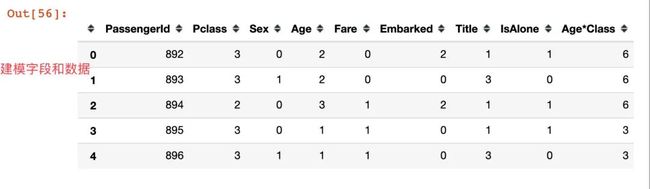
这样我们就得到最终用于建模的字段和数据：

建模

下面是具体的建模过程，我们先划分数据集：

# 训练集
X_train = train.drop("Survived", axis=1)
Y_train = train["Survived"]

# 测试集
X_test  = test.drop("PassengerId", axis=1).copy()
X_train.shape, Y_train.shape, X_test.shape

每个模型的具体过程：

1. 建立模型实例化的对象

2. 拟合训练集

3. 对测试集进行预测

4. 计算准确率

模型1：逻辑回归

# 模型实例化
logreg = LogisticRegression()
# 拟合过程
logreg.fit(X_train, Y_train)

# 测试集预测
Y_pred = logreg.predict(X_test)
# 准确率求解
acc_log = round(logreg.score(X_train, Y_train) * 100, 2)
acc_log

# 结果
81.37

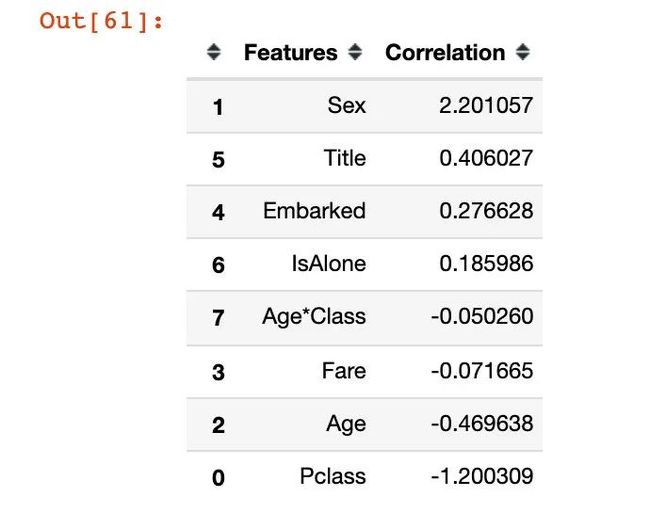
逻辑回归模型得到的系数：

# 逻辑回归特征和系数


coeff_df = pd.DataFrame(train.columns[1:])  # 除去Survived特征
coeff_df.columns = ["Features"]

coeff_df["Correlation"] = pd.Series(logreg.coef_[0])

# 从高到低
coeff_df.sort_values(by='Correlation', ascending=False)

结论：性别对我们的生还真的是一个重要的影响因素

模型2：支持向量机SVM

模型3：KNN

模型4：朴素贝叶斯

模型5：感知机

模型6：线性支持向量分类

linear_svc = LinearSVC()
linear_svc.fit(X_train, Y_train)

Y_pred = linear_svc.predict(X_test)

acc_linear_svc = round(linear_svc.score(X_train, Y_train) * 100, 2)
acc_linear_svc
# 结果
79.46

模型7：随机梯度下降

模型8：决策树

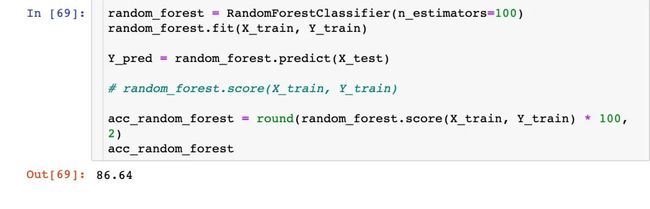
模型9：随机森林

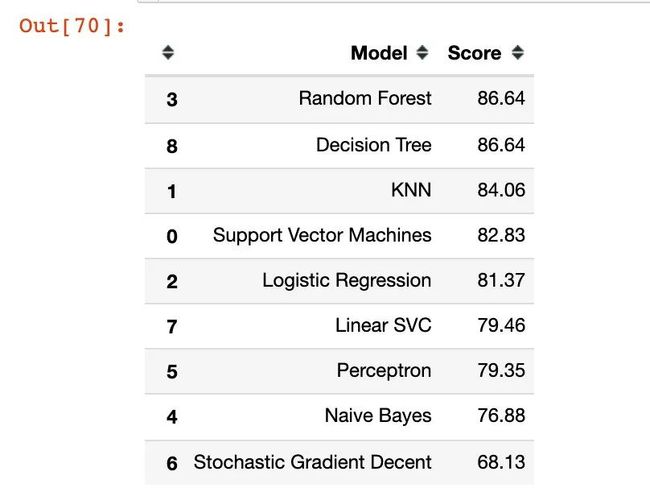
模型对比

将上面9种模型的结果（准确率）进行对比：

models = pd.DataFrame({
    'Model': ['Support Vector Machines', 'KNN', 'Logistic Regression', 
              'Random Forest', 'Naive Bayes', 'Perceptron', 
              'Stochastic Gradient Decent', 'Linear SVC', 
              'Decision Tree'],
    'Score': [acc_svc, acc_knn, acc_log, 
              acc_random_forest, acc_gaussian, acc_perceptron, 
              acc_sgd, acc_linear_svc, acc_decision_tree]})

models.sort_values(by='Score', ascending=False)

通过对比结果：决策树和随机森林在这份数据集表现的效果是最好的；其次就是KNN（K近邻）算法。