LIO-livox - 激光IMU初始化模块分析
激光IMU初始化模块学习
- 概述
- TryMAPInitialization()
-
- 计算初始的先验旋转(world->local)
- 求解MAP优化
- 总结
概述
LIO-LIVOX中激光IMU的初始化的分析梳理。
LIO-LIVOX中激光IMU初始化和ORBSLAM3的视觉惯性初始化类似,都是将初始化问题转换为一个MAP问题求解,
ORBSLAM3相关内容参考ORB_SLAM3 算法框架解析。
总的来说,ORBSLAM3的初始化模块可分为:
1、Vision-only MAP Estimation
2、Inertial-only MAP Estimation
3、Visual-Inertial MAP Estimation
对于激光惯性系统,由于不需要估计特征点的位置,因此,只需要前两步即可:
1、Lidar-only MAP Estimation
2、Inertial-only MAP Estimation
TryMAPInitialization()
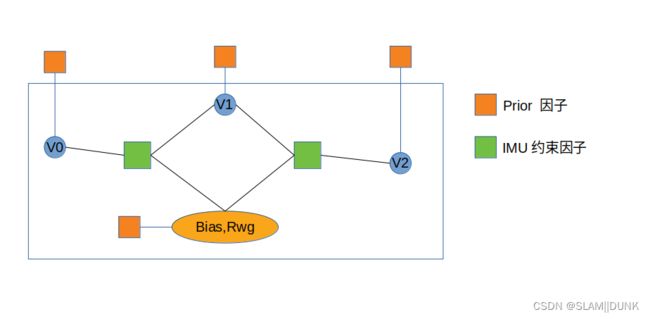
因子图如上图所示。
优化状态为: [ [ v 0 , . . . v n ] , R w b , b a , b ω ] [[v_0,...v_n], R_{wb}, b_a, b_{\omega}] [[v0,...vn],Rwb,ba,bω]
[ v 0 , . . . v n ] [v_0,...v_n] [v0,...vn]是滑窗中n个关键帧imu的速度。
R w b R_{wb} Rwb为滑窗第0帧IMU坐标相对与world系(重力)的旋转。
注意滑动窗口n个帧的局部位姿 [ R b 0 b i , t b 0 b i ] [R_{b_0b_i}, t_{b_0b_i}] [Rb0bi,tb0bi] 不会被优化,而是作为MAP的固定约束,而其值由激光里程计给出。
所有的用于初始化的数据(激光里程计数据,IMU预积分等)保存在lidarFrameList中
boost::shared_ptr
计算初始的先验旋转(world->local)
// 求解IMU加速度的比例因子
Eigen::Vector3d average_acc = -lidarFrameList->begin()->imuIntegrator.GetAverageAcc();
double info_g = std::fabs(9.805 - average_acc.norm());
average_acc = average_acc * 9.805 / average_acc.norm();
// calculate the initial gravity direction
double para_quat[4]; // world -> local 旋转
para_quat[0] = 1;
para_quat[1] = 0;
para_quat[2] = 0;
para_quat[3] = 0;
// 基于ceres求解初始姿态
ceres::LocalParameterization *quatParam = new ceres::QuaternionParameterization();
ceres::Problem problem_quat;
problem_quat.AddParameterBlock(para_quat, 4, quatParam);
problem_quat.AddResidualBlock(Cost_Initial_G::Create(average_acc),
nullptr,
para_quat);
ceres::Solver::Options options_quat;
ceres::Solver::Summary summary_quat;
ceres::Solve(options_quat, &problem_quat, &summary_quat);
Eigen::Quaterniond q_wg(para_quat[0], para_quat[1], para_quat[2], para_quat[3]);
构建最小二乘问题并采用ceres求解 R b w = arg min R b w ∥ R b w G w − A b ∥ 2 R_{bw}=\argmin\limits_{R_{bw}}\|R_{bw}G_w-A_b\|_2 Rbw=Rbwargmin∥RbwGw−Ab∥2
疑问:这貌似是个非凸优化问题吧? 当这样当姿态倾斜比较大时,直接优化能求解的出来??
求解MAP优化
step1: 构建先验约束因子
认为IMU bias保持不变,只有速度V在变化。
IMU bias先验设为0,旋转设置为上一步求解的结果。
// 速度、P、bias先验均为0
Eigen::Vector3d prior_r = Eigen::Vector3d::Zero();
Eigen::Vector3d prior_ba = Eigen::Vector3d::Zero();
Eigen::Vector3d prior_bg = Eigen::Vector3d::Zero();
std::vector<Eigen::Vector3d> prior_v;
int v_size = lidarFrameList->size();
for(int i = 0; i < v_size; i++) {
prior_v.push_back(Eigen::Vector3d::Zero()); // 滑窗内全部速度状态设为0
}
// 旋转先验
Sophus::SO3d SO3_R_wg(q_wg.toRotationMatrix());
prior_r = SO3_R_wg.log(); // world -> local 旋转
重新计算每一帧IMU的速度先验信息,说明不需要保持静止!
for (int i = 1; i < v_size; i++){
auto iter = lidarFrameList->begin();
auto iter_next = lidarFrameList->begin();
std::advance(iter, i-1); // 将迭代器 iter 后退 i-1 步骤
std::advance(iter_next, i);
// 通过 lidar的位置 计算imu的位置 => 计算imu的速度
Eigen::Vector3d velo_imu = (iter_next->P - iter->P + iter_next->Q*exPlb - iter->Q*exPlb)
/ (iter_next->timeStamp - iter->timeStamp);
prior_v[i] = velo_imu;
}
构建优化问题,并设置与先验约束有关的优化状态,添加先验残差factor。
ceres::Problem::Options problem_options;
ceres::Problem problem(problem_options);
problem.AddParameterBlock(para_r, 3); // 旋转
problem.AddParameterBlock(para_ba, 3); // bias
problem.AddParameterBlock(para_bg, 3);
for(int i = 0; i < v_size; i++) {
problem.AddParameterBlock(para_v[i], 3); // 每一帧的速度
}
// add CostFunction 添加先验factor
problem.AddResidualBlock(Cost_Initialization_Prior_R::Create(prior_r, sqrt_information_r),
nullptr,
para_r); // 先验旋转约束
problem.AddResidualBlock(Cost_Initialization_Prior_bv::Create(prior_ba, sqrt_information_ba),
nullptr,
para_ba); // 先验 bias约束
problem.AddResidualBlock(Cost_Initialization_Prior_bv::Create(prior_bg, sqrt_information_bg),
nullptr,
para_bg);// 先验 bias约束
// 先验速度约束
for(int i = 0; i < v_size; i++) {
problem.AddResidualBlock(Cost_Initialization_Prior_bv::Create(prior_v[i], sqrt_information_v),
nullptr,
para_v[i]);
}
step1: 添加IMU预积分约束因子,并求解优化
// 为滑动窗口中每两帧之间添加预积分约束
for(int i = 1; i < v_size; i++) {
auto iter = lidarFrameList->begin();
auto iter_next = lidarFrameList->begin();
std::advance(iter, i-1);
std::advance(iter_next, i);
// 根据激光的位置求解 第i帧 imu的位姿
Eigen::Vector3d pi = iter->P + iter->Q * exPlb;
Sophus::SO3d SO3_Ri(iter->Q*exRlb); // R * Rlb = Rwb
Eigen::Vector3d ri = SO3_Ri.log();
// 根据激光的位置求解 j = i + 1, 第 j 帧 imu的位姿
Eigen::Vector3d pj = iter_next->P + iter_next->Q*exPlb;
Sophus::SO3d SO3_Rj(iter_next->Q*exRlb);
Eigen::Vector3d rj = SO3_Rj.log();
problem.AddResidualBlock(Cost_Initialization_IMU::Create(iter_next->imuIntegrator,
ri, // Rwb
rj,
pj-pi,
Eigen::LLT<Eigen::Matrix<double, 9, 9>>
(iter_next->imuIntegrator.GetCovariance().block<9,9>(0,0).inverse())
.matrixL().transpose()),
nullptr,
para_r,
para_v[i-1],
para_v[i],
para_ba,
para_bg);
}
// 求解优化
ceres::Solver::Options options;
options.minimizer_progress_to_stdout = false;
options.linear_solver_type = ceres::DENSE_QR;
options.num_threads = 6;
ceres::Solver::Summary summary;
ceres::Solve(options, &problem, &summary);
对于第i帧和第j帧IMU,Cost_Initialization_IMU Factor的残差计算如下:
r I i I j 9 × 1 ( R W b 0 , b a , b ω , V b i b 0 , V b j b 0 ) = = ( R b 0 b i ( P b j b 0 − P b i b 0 − V b i b 0 Δ t i j + 0.5 R W b 0 g W Δ t i j 2 ) − ( α I j I i + ∂ α I j I i ∂ δ b a δ b a + ∂ α I j I i ∂ δ b ω δ b ω ) [ ( θ I j I i E x p ( ∂ θ I j I i ∂ δ b ω δ b ω ) ) − 1 ⊗ q b 0 b i ⊗ q b j b 0 ] x y z R b 0 b i ( V b j b 0 − V b i b 0 + R W b 0 g W Δ t i j ) − ( β I j I i + ∂ β I j I i ∂ δ b a δ b a + ∂ β I j I i ∂ δ b ω δ b ω ) ) r_{IiIj}^{9\times1}(R^{b_0}_W,b_a, b_{\omega},V^{b_0}_{b_i},V^{b_0}_{b_j})=\\=\begin{pmatrix} R^{b_i}_{b_0}(P^{b_0}_{b_j}-P^{b_0}_{b_i}-V^{b_0}_{b_i}\Delta t_{ij}+0.5R^{b_0}_Wg^W\Delta t_{ij}^2)-(\alpha^{I_i}_{I_j}+\frac{\partial{\alpha^{I_i}_{I_j}}}{\partial{\delta{b_a}}}\delta{b_a}+\frac{\partial{\alpha^{I_i}_{I_j}}}{\partial{\delta{b_{\omega}}}}\delta{b_{\omega}} ) \\ [(\theta^{I_i}_{I_j} Exp(\frac{\partial{\theta^{I_i}_{I_j} }}{\partial{\delta b_{\omega}}}\delta b_{\omega}))^{-1}\otimes q^{b_i}_{b_0}\otimes q^{b_0}_{b_j}]_{xyz}\\R^{b_i}_{b_0}(V^{b_0}_{b_j}-V^{b_0}_{b_i}+R^{b_0}_Wg^W\Delta t_{ij})-(\beta^{I_i}_{I_j}+\frac{\partial{\beta^{I_i}_{I_j}}}{\partial{\delta{b_a}}}\delta{b_a}+\frac{\partial{\beta^{I_i}_{I_j}}}{\partial{\delta{b_{\omega}}}}\delta{b_{\omega}} ) \end{pmatrix} rIiIj9×1(RWb0,ba,bω,Vbib0,Vbjb0)==⎝ ⎛Rb0bi(Pbjb0−Pbib0−Vbib0Δtij+0.5RWb0gWΔtij2)−(αIjIi+∂δba∂αIjIiδba+∂δbω∂αIjIiδbω)[(θIjIiExp(∂δbω∂θIjIiδbω))−1⊗qb0bi⊗qbjb0]xyzRb0bi(Vbjb0−Vbib0+RWb0gWΔtij)−(βIjIi+∂δba∂βIjIiδba+∂δbω∂βIjIiδbω)⎠ ⎞
其中, P b j b 0 , P b i b 0 , R b 0 b i , R b 0 b j P^{b_0}_{b_j},P^{b_0}_{b_i},R^{b_i}_{b_0},R^{b_j}_{b_0} Pbjb0,Pbib0,Rb0bi,Rb0bj是激光里程计计算出来的位姿,作为已知量传入到残差中,不参与优化。
优化是采用ceres自动求导完成的,因此只需要将上述残差写入factor的operator()重载即可:
/**
* @brief: 自动求导 - 计算残差 的仿函数
* @param rwg_ world - > 滑动窗口第0帧的旋转
* @param vi_ 第i帧速度
* @param vj_ 第j帧速度
* @param ba_ 加速度bias
* @param bg_ 角速度bias
* @param[out] residual 输出结果 残差
* @return {*}
*/
template <typename T>
bool operator()(const T *rwg_, const T *vi_, const T *vj_, const T *ba_, const T *bg_, T *residual) const {
Eigen::Matrix<T, 3, 1> G_I{T(0), T(0), T(-9.805)};
Eigen::Map<const Eigen::Matrix<T, 3, 1>> ba(ba_);
Eigen::Map<const Eigen::Matrix<T, 3, 1>> bg(bg_);
Eigen::Matrix<T, 3, 1> dbg = bg - imu_measure.GetBiasGyr().cast<T>();
Eigen::Matrix<T, 3, 1> dba = ba - imu_measure.GetBiasAcc().cast<T>();
// imu相对与w的旋转
Sophus::SO3<T> SO3_Ri = Sophus::SO3<T>::exp(ri.cast<T>());
Sophus::SO3<T> SO3_Rj = Sophus::SO3<T>::exp(rj.cast<T>());
Eigen::Matrix<T, 3, 1> dP = dp.cast<T>();
Eigen::Map<const Eigen::Matrix<T, 3, 1>> rwg(rwg_);
Sophus::SO3<T> SO3_Rwg = Sophus::SO3<T>::exp(rwg);
Eigen::Map<const Eigen::Matrix<T, 3, 1>> vi(vi_);
Eigen::Matrix<T, 3, 1> Vi = vi;
Eigen::Map<const Eigen::Matrix<T, 3, 1>> vj(vj_);
Eigen::Matrix<T, 3, 1> Vj = vj;
Eigen::Map<Eigen::Matrix<T, 9, 1> > eResiduals(residual);
eResiduals = Eigen::Matrix<T, 9, 1>::Zero();
T dTij = T(imu_measure.GetDeltaTime());
T dT2 = dTij*dTij;
Eigen::Matrix<T, 3, 1> dPij = imu_measure.GetDeltaP().cast<T>(); // imu 预积分量
Eigen::Matrix<T, 3, 1> dVij = imu_measure.GetDeltaV().cast<T>(); // imu 预积分量
Sophus::SO3<T> dRij = Sophus::SO3<T>(imu_measure.GetDeltaQ().cast<T>()); // imu 预积分量
Sophus::SO3<T> RiT = SO3_Ri.inverse(); // Rbw
// 预积分位置残差
// Rbw * (pj - pi - Vwi * t - Rlw * gw *t^2 * 0.5 )
Eigen::Matrix<T, 3, 1> rPij = RiT*(dP - Vi*dTij - SO3_Rwg*G_I*dT2*T(0.5)) -
(dPij + imu_measure.GetJacobian().block<3,3>(IMUIntegrator::O_P, IMUIntegrator::O_BG).cast<T>()*dbg +
imu_measure.GetJacobian().block<3,3>(IMUIntegrator::O_P, IMUIntegrator::O_BA).cast<T>()*dba);
// 预积分姿态残差
Sophus::SO3<T> dR_dbg = Sophus::SO3<T>::exp(
imu_measure.GetJacobian().block<3,3>(IMUIntegrator::O_R, IMUIntegrator::O_BG).cast<T>()*dbg);
Sophus::SO3<T> rRij = (dRij * dR_dbg).inverse() * RiT * SO3_Rj;
Eigen::Matrix<T, 3, 1> rPhiij = rRij.log();
// 预积分速度残差
Eigen::Matrix<T, 3, 1> rVij = RiT*(Vj - Vi - SO3_Rwg*G_I*dTij) -
(dVij + imu_measure.GetJacobian().block<3,3>(IMUIntegrator::O_V, IMUIntegrator::O_BG).cast<T>()*dbg +
imu_measure.GetJacobian().block<3,3>(IMUIntegrator::O_V, IMUIntegrator::O_BA).cast<T>()*dba);
eResiduals.template segment<3>(0) = rPij;
eResiduals.template segment<3>(3) = rPhiij;
eResiduals.template segment<3>(6) = rVij;
// 左乘信息矩阵
eResiduals.applyOnTheLeft(sqrt_information.template cast<T>());
return true;
}
由于对于ceres只能接受残差 r r r,因此,若考虑协方差阵 Σ \Sigma Σ:
∥ r ∥ Σ 2 = r T Σ − 1 r = ( Σ − 1 r ) T Σ − 1 r \|r\|_{\Sigma}^2=r^T\Sigma^{-1} r=(\sqrt{\Sigma^{-1}}r)^T\sqrt{\Sigma^{-1}}r ∥r∥Σ2=rTΣ−1r=(Σ−1r)TΣ−1r
因此构造一个新的残差 r ′ = Σ − 1 r r'=\sqrt{\Sigma^{-1}}r r′=Σ−1r.
总结
这种一种简洁的紧耦合初始化方法,但是需要提前已知IMU与激光的外参,并且也并没有提供时间戳标定,后续可以想想如何加入外参初始化与时间戳对齐的功能…