Normalization总结
Normalization总结
一、BN
全称:Batch Normalization
背景:
随着深度学习网络越来越深,发现深层网络训练起来困难,效果也并没有很好;
这里存在一个问题:内部协变量偏移,也就是每一层的参数变化会影响下一层的参数变化;
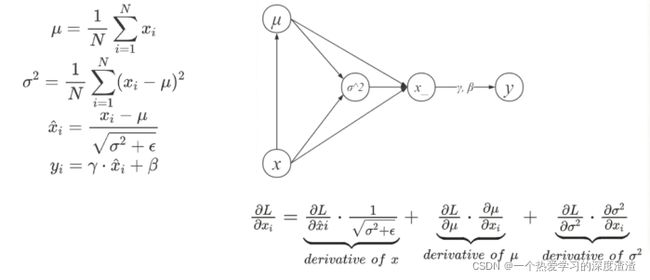
计算公式:
注意:会用到两个参数γ和β,也是在训练时候进行学习的,推理的时候只需要用全局的均值和方差即可;
作用:
引入BN层之后,将各个层之间都进行标准化,起到一个解耦的作用;
优点:
1、提升训练速度,加快收敛过程;
2、起到一个正则化的作用,提升分类效果;
3、调参过程简单;
局限:
1、计算均值和方差是根据一个batchsize计算的,batchsize较小时计算出来的有局限性;
2、要求batchsize是固定的,不适用于动态网络结构或者RNN结构;
注意点:
BN只在训练时候使用,在推理时不会使用;
代码实现:
1、调用torch中封装好的接口
import torch
torch.nn.BatchNorm1d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
torch.nn.BatchNorm3d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
2、手动实现
import torch
from torch import nn
# 创建一个随机矩阵
x = torch.rand(2, 3, 2, 2) * 100
# 使用torch接口计算标准化后的结果
bn = nn.BatchNorm2d(num_features=3, eps=1e-05, momentum=0, affine=False, track_running_stats=False)
pytorch_bn = bn(x)
x1 = x.permute(1, 0, 2, 3).contiguous().view(3, -1)
mu = x1.mean(dim=1).view(1, 3, 1, 1)
std = x1.std(dim=1, unbiased=False).view(1, 3, 1, 1)
my_bn = (x - mu) / std
diff = (pytorch_bn - my_bn).sum()
print('diff={}'.format(diff))
参数说明:
- num_features:代表feature map的channel数量;
- eps:保证数据的稳定性,给分母加上默认值,使得分母不趋近或取0;
- momentum:动态均值和动态方差所用的动量,默认为0.1;
- affine:True的时候添加可学习的仿射变换参数,False的时候只做归一化;
- track_running_stats:True的时候表示训练时候,滑动加权计算均值和方差,False表示测试时候使用;
滑动加权的公式: x ^ new = ( 1 − \hat{x}_{\text {new }}=(1- x^new =(1− momentum ) × x ^ + ) \times \hat{x}+ )×x^+ momentum × x t \times x_{t} ×xt,一定程度上解决batchsize比较小的问题;
思考:
1、Dropout和BN都起到正则化的作用,二者有什么区别?
个人理解:Dropout主要是作用在全连接层之后,BN作用于每一层卷积层之后,随着现在的网络逐渐将全连接层改成全卷积,Dropout使用的频率不多了;并且BN还起到一个加速训练的作用,相比于Dropout来说优点更多;
2、BN放在激活函数前还是激活函数之后?
常规的思想是放在激活函数之前,因为放在之后会破坏激活函数失活的效果;
3、BN的反向传播公式推导?
通过下面的图可以理解,通过链式法则进行推导;
最终求导出来的结果:
∂ L ∂ x i = ∂ L ∂ x ^ i ⋅ 1 σ 2 + ϵ + ∂ L ∂ μ ⋅ 1 N + ∂ L ∂ σ 2 ⋅ 2 ( x i − μ ) N \frac{\partial L}{\partial x_{i}}=\frac{\partial L}{\partial \hat{x}_{i}} \cdot \frac{1}{\sqrt{\sigma^{2}+\epsilon}}+\frac{\partial L}{\partial \mu} \cdot \frac{1}{N}+\frac{\partial L}{\partial \sigma^{2}} \cdot \frac{2\left(x_{i}-\mu\right)}{N} ∂xi∂L=∂x^i∂L⋅σ2+ϵ1+∂μ∂L⋅N1+∂σ2∂L⋅N2(xi−μ)
二、LN
全称:Layer Normalization
作用:
解决BN层无法作用于RNN结构等问题;
代码实现:
1、调用toch库中自带的接口
torch.nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True)
2、手动实现
import torch
from torch import nn
x = torch.rand(10, 3, 2, 2) * 100
# 调用接口计算LN后的值
ln = nn.LayerNorm(normalized_shape=[3, 2, 2], eps= 1e-05, elementwise_affine=False)
pytorch_ln = ln(x)
x1 = x.view(10, -1)
mu = x1.mean(dim=1).view(10, 1, 1, 1)
std = x1.std(dim=1, unbiased=False).view(10, 1, 1, 1)
my_ln = (x - mu) / std
diff = (my_ln - pytorch_ln).sum()
print('diff={}'.format(diff))
说明:可以看出这里计算的维度是针对每个样本,而不是一个batch;
下面通过两个图对比下BN和LN的不同之处:
三、IN
全称:Instance Normalization
作用:
一般在图像风格迁移任务才会使用,目的是为了让图像更接近原图的风格,只对H和W维度计算均值和方差;
代码实现:
1、使用torch自带接口
torch.nn.InstanceNorm1d(num_features, eps=1e-05, momentum=0.1, affine=False, track_running_stats=False)
torch.nn.InstanceNorm2d(num_features, eps=1e-05, momentum=0.1, affine=False, track_running_stats=False)
torch.nn.InstanceNorm3d(num_features, eps=1e-05, momentum=0.1, affine=False, track_running_stats=False)
2、手动实现
import torch
from torch import nn
# 创建一个随机矩阵
x = torch.rand(5, 3, 2, 2) * 100
In = nn.InstanceNorm2d(num_features=3, eps=0, affine=False, track_running_stats=False)
pytorch_in = In(x)
x1 = x.view(15, -1)
# 这里需要用到H和W维度
mu = x1.mean(dim=1).view(5, 3, 1, 1)
std = x1.std(dim=1, unbiased=False).view(5, 3, 1, 1)
my_in = (x-mu) / std
diff = (my_in-pytorch_in).sum()
print('diff={}'.format(diff))
四、GN
全称:Group Normalization(组归一化)
背景:
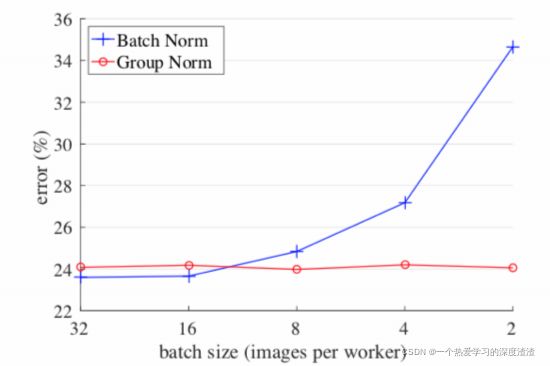
先来看一下BN在不同batchsize下对于误差的影响:
说明:在Batchsize较小的情况下,BN的误差会比较大,所以提出GN这种新的Normalization方法;
作用:
解决由于显存不足,batchsize较小存在的问题;
代码实现:
1、torch自带接口实现
torch.nn.GroupNorm(num_groups, num_channels, eps=1e-05, affine=True)
2、手动实现
import torch
from torch import nn
# 创建一个随机矩阵
x = torch.rand(5, 10, 3, 3) *100
gn = nn.GroupNorm(num_groups=2, num_channels=10, eps=0, affine=False)
pytorch_gn = gn(x)
# 组数设置为2
x1 = x.view(5, 2, -1)
mu = x1.mean(dim=-1).reshape(5, 2, -1)
std = x1.std(dim=-1).reshape(5, 2, -1)
x1_norm = (x1 - mu) / std
my_gn = x1_norm.reshape(5, 10, 3, 3)
diff = (my_gn - pytorch_gn).sum()
print('diff={}'.format(diff))
五、拓展
集成以上四种归一化的方法,引出了Switchable Normalization;
实际上就是根据不同的任务采用多了Norm方法,并且进行加权;
上图为实验中采用的加权方式;
这里也可是手动实现一下代码:
import numpy as np
def SwitchableNorm(x, gamma, beta, w_mean, w_var):
eps = 1e-5
mean_in = np.mean(x, axis=(2, 3), keepdims=True)
var_in = np.var(x, axis=(2, 3), keepdims=True)
mean_ln = np.mean(x, axis=(1, 2, 3), keepdims=True)
var_ln = np.var(x, axis=(1, 2, 3), keepdims=True)
mean_bn = np.mean(x, axis=(0, 2, 3), keepdims=True)
var_bn = np.var(x, axis=(0, 2, 3), keepdims=True)
mean = w_mean[0] * mean_in + w_mean[1] * mean_ln + w_mean[2] * mean_bn
var = w_var[0] * var_in + w_var[1] * var_ln + w_var[2] * var_bn
x_normalized = (x - mean) / np.sqrt(var + eps)
results = gamma * x_normalized + beta
return results
x = np.random.rand(5, 10, 3, 3) * 100
y = SwitchableNorm(x, 0.1, 0.1, [0.1, 0.1, 0.8], [0.01, 0.02, 0.05])
六、总结
BatchNorm:batch方向上做归一化,算NHW的均值,对小batchsize效果不好;
LayerNorm:channel方向做归一化,算CHW的均值,主要对RNN作用明显;
InstanceNorm:一个channel方向做归一化,算HW的均值,主要用在风格迁移;
GroupNorm:将channel方向分group,然后每一个group内做归一化,算(C//G)HW的均值,这样就与batchsize无关,不受batchsize约束;
SwitchableNorm:将BN、LN、IN结合,赋予权重,让网络自主学习用什么方法;