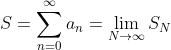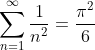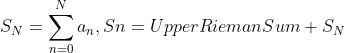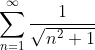第五单元 用python学习微积分（三十三）反常积分（下）-- 无穷级数和收敛判定
本文内容来自于学习麻省理工学院公开课：单变量微积分-无穷级数和收敛判定-网易公开课
Bullseye：第一单元 用python学习微积分（一） 安装开发环境Anaconda 和 导数（上）- 1/x的导数
Bullseye：第五单元 用python学习微积分（三十二）无穷的处理--不定式（下）和反常积分
芝诺悖论_百度百科
一、第二种类型的反常积分
1、定义
如果极限存在就是收敛的否则就是不收敛的，
2、例1
积分是收敛的
import numpy as np
from sympy import *
import matplotlib.pyplot as plt
figure, ax= plt.subplots( 1 )
ax.set_aspect( 1 )
def DrawXY1(xFrom,xTo,steps,expr,color,label,plt, arrow =False):
yarr = []
xarr = np.linspace(xFrom ,xTo, steps)
for xval in xarr:
#print(expr.subs(x,xval), xval)
yval = expr.subs(x,xval)
yarr.append(yval)
y_nparr = np.array(yarr)
x_nparr = np.array(xarr)
length = len (xarr)
plt.plot(x_nparr, y_nparr, c=color, label=label)
if(arrow and steps > 2):
plt.arrow(float(x_nparr[0]),float( y_nparr[0]),float( x_nparr[2]-x_nparr[0]),float( y_nparr[2]-y_nparr[0]), width=.02, color = color)
def DrawXY(tFrom,tTo,steps,exprX,exprY, color,label,plt, arrow =False):
xarr = []
yarr = []
tarr = np.linspace(tFrom ,tTo, steps)
for tval in tarr:
xval = exprX.subs(t,tval)
xarr.append(xval)
yval = exprY.subs(t,tval)
yarr.append(yval)
y_nparr = np.array(yarr)
x_nparr = np.array(xarr)
length = len (xarr)
plt.plot(x_nparr, y_nparr, c=color, label=label)
if(arrow and steps > 2):
plt.arrow(float(x_nparr[0]),float( y_nparr[0]),float( x_nparr[2]-x_nparr[0]),float( y_nparr[2]-y_nparr[0]), width=.02, color = color)
x = symbols('x')
expr = 1/(x**0.5)
DrawXY1( 0.1,1,50,expr,color='c', label=' 1/(x**0.5)',plt = plt, arrow = False)
plt.legend(loc='lower right')
plt.show()
3、例2
（1）临界情况（border line）
积分是发散的
（2）上节课给出的
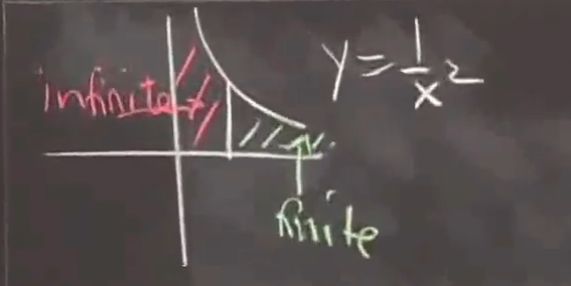
当 0 当 p>1时 对比： 当 当 如下图， 1/x 如下图， 如下图， 二、无限级数 1、例1 关于这个级数，老师提到了芝诺悖论。当兔子追逐乌龟，它会先到达总距离的一半，而后它又会先到达当前距离的一半，而后又是一半的一半, 如此类推，它永远都无法追上乌龟。老师说这个悖论的结论是没有时间。确是如此，芝诺只考虑了距离是无限可分的，但是没有考虑通过这段距离的时间，也即是没有考虑速度。 2、几何级数的一般情况 当 -1 当 a = 1 时 当 a -1 时 当a=2时， 3、注意 级数的部分和： 级数的总和： 这里 （1）极限存在，即级数收敛（series converges） （1）极限不存在，即级数发散（series diverges） 4、例2 首先我们知道 5、例3 6、例4 从上图中可以看到在（ （1）黎曼上和（ 由 （2）黎曼上和的面积显然要大于 由 （3）当使用黎曼下和（ 从上图可知： 由上： 综合上面得到的结果 ： 7、积分比较 如果f(x)据x增长递减，同时是正数，则有 8、极限比较（Limit Comparison） 如果 则 9、例5 找到对应的 10、例6 找到对应的 由于积分中 所以 
(函数的积分是发散的：
)
(函数的积分是发散的： 
)
在两个取值空间都是发散的：
在两个取值空间有不同的情况：
x = symbols('x')
expr = 1/(x**0.5)
DrawXY1( 0.1,1,50,expr,color='c', label=' 1/(x**0.5)',plt = plt, arrow = False)
DrawXY1( 1,4,50,expr,color='blue', label='',plt = plt, arrow = False)
expr = 1/x
DrawXY1( 0.1,5,50,expr,color='r', label=' 1/x)',plt = plt, arrow = False)
DrawXY1( 1.4,5,50,expr,color='orange', label='',plt = plt, arrow = False)
plt.legend(loc='lower right')
plt.show()plt.showx = symbols('x')
expr = 1/(x**0.5)
DrawXY1( 0.1,1,50,expr,color='c', label=' 1/(x**0.5)',plt = plt, arrow = False)
DrawXY1( 1,4,50,expr,color='blue', label='',plt = plt, arrow = False)
expr = 1/x
DrawXY1( 0.1,5,50,expr,color='r', label=' 1/x)',plt = plt, arrow = False)
DrawXY1( 1.4,5,50,expr,color='orange', label='',plt = plt, arrow = False)
plt.legend(loc='lower right')
plt.show()
在两个取值空间有不同的情况：
def DrawPowerInfiniteSeriesXY1(base,steps,color,label,plt, arrow =False):
yarr = []
xarr = []
def PowerInfiniteSeries(oldValue,base, power):
return base**power
yval = 0
for xval in range(steps):
xarr.append(xval)
yval += PowerInfiniteSeries(yval,base,xval)
yarr.append(yval)
y_nparr = np.array(yarr)
x_nparr = np.array(xarr)
length = len (xarr)
plt.plot(x_nparr, y_nparr, c=color, label=label)
if(arrow and steps > 2):
plt.arrow(float(x_nparr[0]),float( y_nparr[0]),float( x_nparr[2]-x_nparr[0]),float( y_nparr[2]-y_nparr[0]), width=.02, color = color)
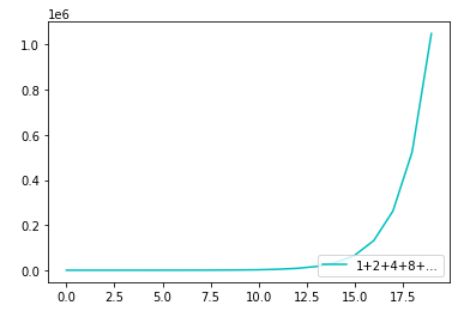
DrawPowerInfiniteSeriesXY1(0.5,20,color='c',label='1+1/2+1/4+1/8+...',plt=plt, arrow =False)
plt.legend(loc='lower right')
plt.show()
（收敛的）
（发散的）DrawPowerInfiniteSeriesXY1(1,20,color='c',label='1+1+1+1+...',plt=plt, arrow =False)
plt.legend(loc='lower right')
plt.show()
（通过公式算出结果是
，但实际上结果是 0 或 -1 ，所以结果依旧是发散的）DrawPowerInfiniteSeriesXY1(1,20,color='c',label='1-1+1-1...',plt=plt, arrow =False)
plt.legend(loc='lower right')
plt.show()
（用公式 \frac{1}{1-a} 计算的结果是收敛的，实际上等式左侧的值是发散的。额外需要指出的是，老师在这说在数论中存在这样的系统让等式右边的结果成立）
有两种情况：
对应积分
（收敛）
(计算这个需要很有技巧，老师直接给答案了)
对应积分
（收敛）困扰数学界很久，不久前被证明是无理数
对应积分 
（ 发散的 ）def DrawRiemanSum(isUpper,xFrom,xTo,steps,expr,color,label,plt):
length = (xTo - xFrom)/steps
xarrRect = []
yarrRect = []
area = 0
xprev = xFrom
for step in range(steps):
if(not isUpper):
yval = expr.subs(x,xprev +length)
else:
yval = expr.subs(x,xprev )
xarrRect.append(xprev)
xarrRect.append(xprev)
xarrRect.append(xprev + length)
xarrRect.append(xprev + length)
yarrRect.append(0)
yarrRect.append(yval)
yarrRect.append(yval)
yarrRect.append(0)
area += length * yval
plt.plot(xarrRect, yarrRect, c=color, label=label)
xprev= xprev + length
x = symbols('x')
expr = 1/x
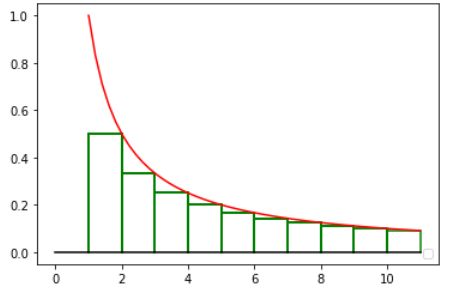
DrawRiemanSum(True,1,11,10,expr,color='g',label='',plt=plt)
DrawXY1( 1,11,50,expr,color='r',label= '',plt = plt, arrow = False)
plt.plot([0,11], [0,0], c='black', label='')
plt.legend(loc='lower right')
plt.show()
）区间：
） 
曲线下面的面积(即的积分)，则有
可知
（是发散的）x = symbols('x')
expr = 1/x
DrawRiemanSum(False,1,11,10,expr,color='g',label='',plt=plt)
DrawXY1( 1,11,50,expr,color='r',label= '',plt = plt, arrow = False)
plt.plot([0,11], [0,0], c='black', label='')
plt.legend(loc='lower right')
plt.show()
）时，
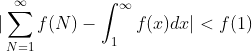， 同时有，和式和积分式同时收敛或发散。
， g(n)>0 ,
和 
同时收敛或发散。
，它的积分式
是发散的， 所以是发散的
，它的积分式
的幂
,所以 是收敛的是收敛的